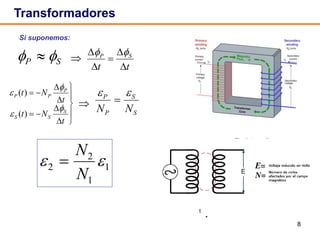
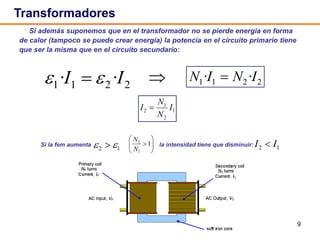
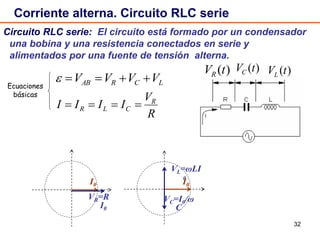
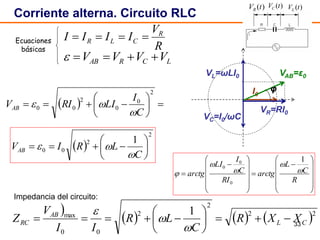
Este documento describe los circuitos de corriente alterna formados por resistencias, condensadores e inductancias conectados a un generador de tensión alterna. Explica que en un circuito RC la corriente presenta un adelanto de fase de π/2 respecto a la tensión en el condensador, mientras que en un circuito RL la corriente presenta un retraso de fase de π/2 respecto a la tensión en la inductancia. También define conceptos como reactancia, impedancia y desfase para estos circuitos.

1. 1
animación
Cuando veas este icono púlsalo
para observar una animación que
aparecerá en tu explorador video
Cuando veas este icono púlsalo
para observar una vídeo que
aparecerá en tu explorador
Circuitos de
corriente Alterna.

2. 2
Generador. Producción de Corriente alterna.
Si hacemos girar una espira en el interior de un
campo magnético (B), aproximadamente uniforme se
inducirá en ella una fuerza electromotriz y por tanto
una corriente eléctrica.
Esta corriente está cambiando continuamente en el
tiempo.
La corriente cambia en magnitud y signo.
Animacion1
Este principio es utilizado en el generador electromagnético para
producir corriente alterna.
Es un ejemplo clásico de transformación de energía mecánica (del
movimiento) en energía eléctrica

3. 3
Generador. Producción de Corriente alterna.
s el área de la espira
α el ángulo entre B y la dirección normal de la espira. varía de 0º a 360º .
Expresando el ángulo girado en función de la velocidad angular de giro
ω•t representa el ángulo girado en radianes,
ω la velocidad angular en rad/s.
 cosBS
tBSt  cos
Si hacemos girar una espira en el interior de un
campo magnético (B), aproximadamente
uniforme. El flujo magnético que la atraviesa
será:

4. 4
Generador. Producción de Corriente alterna.
Expresando el ángulo girado en función de la velocidad angular de giro
ω•t representa el ángulo girado en radianes,
ω la velocidad angular en rad/s.
Por lo tanto en la espira se inducirá una fuerza electromotriz de valor:
Si la bobina tiene N espiras:
tBSt  cos
tBSsen
dt
d
t 

 )(
tNBSsent  )(

5. 5
Generador. Producción de Corriente alterna.
Si mantenemos constante la inducción del campo y la velocidad de giro,
siéndolo también el número de espiras y el área de las mismas, tendremos:
Como puede verse en la fórmula la f.e.m. resultante tendrá forma senoidal.
cteNBS max
tsent  max)( 

6. 6
Generadores de corriente
Generadores de corriente AC: Alternador
animación
Si no te funciona la animación
de esta página pulsa este icono

7. 7
Generadores de corriente
Generadores de corriente DC: Dinamo
animación
Si no te funciona la animación
de esta página pulsa este icono

8. 8
Transformadores
SP  











t
Nt
t
Nt
S
SS
P
PP




)(
)(

S
S
P
P
NN


1
1
2
2 
N
N

Si suponemos:
tt
SP




 

t

9. 9
Transformadores
Si además suponemos que en el transformador no se pierde energía en forma
de calor (tampoco se puede crear energía) la potencia en el circuito primario tiene
que ser la misma que en el circuito secundario:
2211 ·· II   2211 ·· ININ 
Si la fem aumenta la intensidad tiene que disminuir:
1
2
1
2 I
N
N
I 
12   





1
1
2
N
N
12 II 

10. 10
Corriente alterna.
Toda corriente eléctrica cuya intensidad varía en el tiempo su valor y sentido
de forma periódica .
 De todas las posibilidades la más importante (por sus aplicaciones tecnoló-
gicas) es la corriente alterna sinusoidal.
tsent  0)( 
)()( 0   tsenItI 



 
AmplitudI
inicialfase
frecuencia
T
f
0
22



11. 11
Autoinducción

Li 

12. 12
Un circuito de corriente alterna consiste en la conexión de varios elementos:
 Resistencias (R):
Capacidades (C):
Autoinducciones (L):
y un generador:
que suministra una fem alterna. Además de las resistencias (R) los nuevos
elementos (C y L) también influyen en el valor de la intensidad
Circuitos de corriente alterna.
)(·)( tvCtQ C )(tvC
Q Q
 (t)vR
)(·)( tiRtvR 
 )(tvL
dt
tdi
LtvL
)(
)( 
tsent  0)( 

13. 13
Una magnitud alterna senoidal tiene una expresión matemática:
FASORES (ver paginas 19-20 de los apuntes)
)()( 0   tsenVtv
y su representación gráfica corresponde a la proyección sobre el eje vertical
de un vector VMAX que gira con velocidad angular ω.
A este tipo de representación se le llama “representación fasorial o de Fresnel”

14. 14
Corriente alterna. Circuito R (El más simple)
Circuito R (El más simple):
)(tvR)(t
)(
)(
)( 0 tsenI
R
tv
ti R

R
I 0
0


La corriente será, como la tensión , de tipo alterna senoidal.
Además, la corriente y la tensión tienen la misma frecuencia y fase (están
en fase)
)()( 0 tvtsent R 

15. 15
Corriente alterna. Circuito R (El más simple)
Circuito R (El más simple):
)(tVR)(t
)(
)(
)( 0 tsenI
R
tv
ti R

R
I 0
0



16. 16
Circuito R. Representación fasorial
animación
Si no te funciona la animación
de esta página pulsa este icono

17. 17
Circuito C: El circuito formado por un condensador alimentado
por una fuente de tensión alterna sinuoidal.
Un condensador no permite el “paso” de la corriente continua, en cambio, si
que permite el “paso” de la corriente alterna1.
En este caso la corriente y la tensión tienen la misma frecuencia pero I(t)
presenta un adelanto de fase de pi/2 frente a Vc(t) .
1Si la fem es alterna está cambiando continuamente su polaridad y las armaduras del condensador se
va cargando y descargando sucesivamente, “permite” el paso de la corriente alterna aunque no lo
hace de forma instantánea, presenta cierta resistencia (cierta inercia) al paso de ésta
Corriente alterna. Circuito C
)(tvC
)(t
)·()()()( 0 tsenCtCtCvtQ C  
)cos(
)())(()(
0 tC
dt
td
C
dt
tCd
dt
tdQ



)(
)(
ti
dt
tdQ

 20·)( 
  tsenIti 00 CI 

18. 18
En este circuito el condensador presentará una oposición al paso de la
corriente alterna.
Dicha oposición se llama reactancia capacitiva , su unidad en el SI es el
Ohmio (Ω) y se define como el cociente entre los valores máximos de V e I:
Corriente alterna. Circuito C
CCI
XC

 1
0
0
0
0




I(t) “va por delante” π/2
(llega antes)

19. 19
Circuito C. Representación fasorial
animación
Si no te funciona la animación
de esta página pulsa este icono

20. 20
Circuito L: El circuito está formado por una autoinducción
alimentada por una fuente de tensión alterna.
En este caso la corriente y la tensión tienen la misma frecuencia pero I(t)
presenta un retraso de fase de pi/2 frente a VL(t) .
Corriente alterna. Circuito L
dt
tdi
Lt
)(
)( 
)()( 20

  tsenIti
L
I

0
0 
)cos()( 0
t
L
ti 



)(tVL)(t
I(t) “va detrás” π/2
(llega después)

21. 21
En este circuito la autoinducción presentará una oposición al paso de la
corriente alterna.
Dicha oposición se llama reactancia inductiva , su unidad en el SI es el Ohmio
(Ω) y se define como el cociente entre los valores máximos de V e I :
Corriente alterna. Circuito L
L
I
XL 


0
0

22. 22
Circuito L. Representación fasorial
animación
Si no te funciona la animación
de esta página pulsa este icono

23. 23
2. Una bobina de 100mH se conecta a un generador de fem igual a 125V y
frecuencia 70Hz. Calcula:
a. La reactancia inductiva
b. La corriente (máxima) en el circuito
Sol:
1.Calcular la reactancia capacitiva de un condensador de 2μF cuando la
frecuencia de la corriente alterna es de 100 Hz.
Sol:
Ejemplos
 795,8CX
3. Un condensador de 10μF se conecta a un generador de fem máxima igual a
220V y frecuencia 50Hz. Calcula:
a. La reactancia inductiva
b. La corriente (máxima) en el circuito
Sol:
AIXL 8,2,44 


CI
XC
1
0
0

L
I
XL 


0
0
AIXC 7,0,3,318 


CI
XC
1
0
0


24. 24
Circuito RC serie: El circuito está formado por un condensador y una
resistencia conectados en serie y alimentados por una fuente de
tensión alterna.
Corriente alterna. Circuito RC
CRAB vvv 
B
A
)(tvR
)(tvC
VR=RI0
I0
VC=I0/ωC
I0
I tiene un adelanto de fase
respecto de VC
2

C
I
V C
C

I y VR están en fase
RR RIV 
Ecuaciones básicas:
R
tv
tititi R
CR
)(
)()()( 

25. 25
Corriente alterna. Circuito RC
I0
VC=I0/ωC
VR=RI0
VAB=ε0
Δφ  




 

2
02
00
C
I
RIVAB


















 

CR
arctg
RI
C
I
arctg


1
0
0
 
2
2
00
1





 

C
RIVAB



     22
2
2
00
max 1
C
AB
RC XR
C
R
II
V
Z 




 



Impedancia del circuito:
CRAB vvv 
Ecuaciones básicas:
R
tv
tititi R
CR
)(
)()()( 
Desfase:
B
A
Circuito RC serie: El circuito está formado por un condensador (C)
y una resistencia (R) conectados en serie y alimentados por una
fuente de tensión alterna.

26. 26
Corriente alterna. Circuito RC
















 

CR
arctg
RI
C
I
arctg


1
0
0

     22
2
2
00
max 1
C
AB
RC XR
C
R
II
V
Z 




 




27. 27
Circuito RC. Representación fasorial
animación
Si no te funciona la animación
de esta página pulsa este icono

28. 28
 4 Un circuito eléctrico está formado por una resistencia de 40Ω y un
condensador de capacidad 20 μF en serie con un generador de corriente
alterna de fem máxima 120V y frecuencia f=50Hz. Calcula:
a. La impedancia del circuito.
b. La diferencia de fase entre la fem y la intensidad.
c. La expresión de la intensidad instantánea.
Sol:
Ejemplos
Atsenti
radZ
)32,1100(73,0)(
32,1,1,164





     22
2
2
00
max 1
C
AB
RC XR
C
R
II
V
Z 




 



















 

CR
arctg
RI
C
I
arctg


1
0
0

29. 29
Circuito RL serie : El circuito está formado por una resistencia (R) y una
autoinducción (L) conectadas en serie y alimentadas por una fuente de
tensión alterna.
Corriente alterna. Circuito RL
)()()()( tvtvtvt LRAB 
B
A
)(tvR
)(tvL
VR=RI0
I0
I tiene un retraso de fase de
respecto de VL
2

LL ILV ·
I y VR están en fase en la
RR RIV 
VL=ωLI0
I0
Ecuaciones básicas:
R
tv
tItiti R
LR
)(
)()()( 

30. 30
Corriente alterna. Circuito RL
    
2
0
2
00 LIRIVAB 













R
L
arctg
RI
LI
arctg


0
0
   22
00 LRIVAB  

       2222
00
max
L
AB
RL XRLR
II
V
Z  

Δφ
I0 VR=RI0
VAB=ε0
VL=ωLI0
Impedancia del circuito:
Ecuaciones básicas:
)()()()( tvtvtvt LRAB 
R
tv
tItiti R
LR
)(
)()()( 
Desfase:

31. 31
Un circuito formado por una resistencia de 6 ohmios en serie con una
bobina de autoinducción L = 0.3 H y resistencia despreciable, está
conectado a un generador de corriente alterna cuya tensión eficaz es de
40 V y la frecuencia de 100 Hz. Hallar:
a) la inductancia de la bobina
b) el desfase entre la tensión del generador y la intensidad.
c) lo valores instantáneos de la tensión entre los bornes de la resistencia y
entre los bornes del conjunto.
Ejemplos
Atsenti
radZ
)54,1200(30,0)(
54,1,6,188




)·200(·6,56)·()( 0 tsentsent  
VVV efMax 6,5640
2
2
2
2

Datos:
f 100
w(omega) (rad/s) 628,3185307
Tension máxima del
generador (Eo) 56,56854249
R (Ohmios) 6
L (Henrios) 0,3
C (Faradios, F) 1E+37
Capacitancia (Ohmios) 1,59155E-40
Inductancia (Ohmios) 188,4955592
Impedancia del
circuito (Ohmios) 188,591028
desfase (I,V) (rad) 1,538976082
Intensidad maxima Io
(A) 0,299953519
)54,1·200(·30,0·6)(·)(  tsentiRtVR 
)cos(·
)(
·)(
30,0·100·200··
00
000




tIL
dt
tdi
LtV
ILIXV
L
LL

32. 32
Circuito RLC serie: El circuito está formado por un condensador
una bobina y una resistencia conectados en serie y
alimentados por una fuente de tensión alterna.
Corriente alterna. Circuito RLC serie
LCRAB VVVV 
R
V
IIII R
CLR 
)(tVR
)(tVC )(tVL
VL=ωLI
0
I0
VC=I0/ω
C
VR=R
I0
I0
Ecuaciones
básicas

33. 33
Corriente alterna. Circuito RLC
  






2
0
0
2
00
C
I
LIRIVAB






























R
C
L
arctg
RI
C
I
LI
arctg 




1
0
0
0
 
2
2
00
1







C
LRIVAB



     22
2
2
00
max 1
CL
AB
RC XXR
C
LR
II
V
Z 









Impedancia del circuito:
)(tVR
)(tVC )(tVL
LCRAB VVVV 
R
V
IIII R
CLR 
I0
VR=RI0
VAB=ε0
φ
VL=ωLI0
VC=I0/ωC
Ecuaciones
básicas

34. 34
Circuito RLC. Representación fasorial
animación
Si no te funciona la animación
de esta página pulsa este icono

35. 35
5. Un circuito eléctrico está formado por una resistencia de 40Ω, un
condensador de capacidad 30 μF y una bobina de autoinducción igual
a 0,6H en serie con un generador de corriente alterna de fem máxima
200V y frecuencia f=60Hz. Calcula:
a. La impedancia del circuito.
b. La diferencia de fase entre la fem y la intensidad.
c. La expresión de la intensidad instantánea.
Sol:
Ejemplos
Atsenti
radZ
)3,1120(4,1)(
3,1,5,143




Datos:
w(omega) (rad/s) 376,9911184
Tension máxima del
generador (Eo) 200
R (Ohmios) 40
L (Henrios) 0,6
C (Faradios, F) 0,00003
Capacitancia (Ohmios)88,41941283
Inductancia
(Ohmios) 226,1946711
Impedancia del
circuito (Ohmios) 143,4643572
desfase (I,V) (rad) 1,288236478
Intensidad maxima
Io (A) 1,394074486

36. 36
POTENCIA en un circuito DC
R
IVItvtitP
2
0000
0
··)()·()(

 
00
00
·
··
)( VI
T
TVI
T
Area
t
Area
t
E
tPm 





Circuito R:
f(x)=2
Shade 1
t
P(t)
V0·I0
Δt
El Area debajo de la curva es la
energia suministrada por la fuente
al circuito
Potencia instantánea:
Potencia media:






T
m dttti
TT
Area
t
Area
t
E
tP
0
)()·(
1
)( 
AreaTVIttPE  ··)·( 00
 
TT
dtttidttPArea
00
)()·()( 

37. 37
t
P(t)
(V0·I0)/2
POTENCIA en un circuito AC
)()·()( tvtitP 
 )()·()()·()( 00 tsentsenIttitP   )2cos(1
2
)(2
 
A
Asen
 )2cos(1
2
)()·()( 00
t
I
ttitP 

 
2
)()·(
1
)( 00
0


I
dttti
T
tP
T
m  
Circuito R (El más simple):
En este caso la potencia instantánea tendrá 2 componentes: una constante y la otra
periódica (con un periodo la mitad que el de la tensión –una frecuencia doble-)
Potencia instantánea:
Potencia media:
Termino constante
2
00VI
Tensión tsent  0)( 
Término periódico )2cos(
2
· 00
t
I



38. 38
POTENCIA en un circuito AC
)()·()( tvtitP 
 

)cos()cos(
2
)()·()()·()(
00
00
000
tttt
I
tsentsenIttitP



 )cos()cos(
2
)()·(  
A
senAsen
 )2cos()cos(
2
)()·()( 00
00


  t
I
ttitP
)cos(
2
)()·(
1
)( 0
00
0



I
dttti
T
tP
T
m  
Circuito RLC:
*Nota:
(*)
Potencia instantánea:
Potencia media:

39. 39
POTENCIA en un circuito AC
)()·()( tvtitP 
)cos(
2
)()·(
1
)( 0
00
0



I
dttti
T
tP
T
m  
Circuito RLC:
Potencia instantánea:
Potencia media:







RLCcircuitos
LoCcircuitos
Rcircuito
1)cos(0
0
1
)cos(
0
0


Factor de potencia:

40. 40
POTENCIA en un circuito AC
 )cos()cos(
2
)()·(  
A
senAsen
 )2cos()cos(
2
)()·()( 00
00


  t
I
ttitP
)cos(
2
)()·(
1
)( 0
00
0



I
dttti
T
tP
T
m  

41. 41
POTENCIA en un circuito AC
)()·()( tvtitP 
 )2cos()cos(
2
)()·()( 00
00


  t
I
ttitP
)cos(
2
)()·(
1
)( 0
00
0



I
dttti
T
tP
T
m  

42. 42
Un circuito eléctrico está formado por una resistencia de 100Ω, un condensador de
capacidad 2 μF y una bobina de autoinducción igual a 100 mH en serie con un generador
de corriente alterna de fem máxima 50V y frecuencia f=500Hz. Calcula:
a. La impedancia del circuito y la diferencia de fase entre la fem y la intensidad.
b. La expresión de la intensidad instantánea.
c. La frecuencia de resonancia y la intensidad máxima del circuito en esta situación.
d. La potencia media consumida por el circuito
Sol:
Ejemplos
a)
Tension máxima del
generador (Eo) 50
R (Ohmios) 100
L (Henrios) 0,1
C (Faradios, F) 2,00E-06
Resultados
Capacitancia (Ohmios) 159,1549431
Inductancia (Ohmios)
314,1592654
Impedancia del circuito
(Ohmios) 184,4622995
desfase (I,V) (rad) 0,997842887 2236,067977
Intensidad maxima Io (A) 0,271058098 100
0,5
Impedancia (en resonancia)
Intensidad máxima (en
resonancia) A
NOTA: Si el problema no tiene L poner 0 en el valor de
la autoinducción. Si el problema no tiene condensador
poner un número muy grande (>10exp20) en el valor de
C
NOTA 2: Si quieres poner algún valor con potencias de
10 escribelo así: Por ejemplo "8X10 elevado a menos 3"
es: 8E+3
Resonancia
Frecuencia de resonancia

43. 43
Formulario circuitos de corriente alterna

44. 44
Tablas con magnitudes
VALOR
INSTANTANEO:
VELOCIDAD
ANGULAR:
En rad/s.
(También llamada pulsación).
ANGULO
GIRADO:
En radianes
(la calculadora en RAD).
PERIODO:
En segundos
(tiempo que dura un ciclo).
FRECUENCIA: (Número de ciclos en un segundo). En
hercios (Hz) o ciclos/segundo.
VALOR MAXIMO: Valor máximo, de pico o de cresta.
VALOR PICO A
PICO:
Valor doble del valor máximo.
VALOR MEDIO:
Media algebraica de un semiperiodo.
(La media de un periodo es cero).
VALOR EFICAZ[1]
:
Media cuadrática de un periodo.
Representa el valor que aplicado de forma
continua sobre una resistencia disipa en ella
la misma potencia.