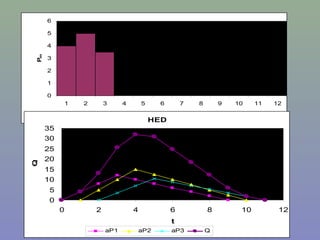
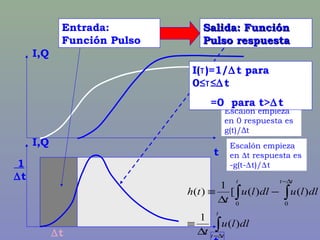
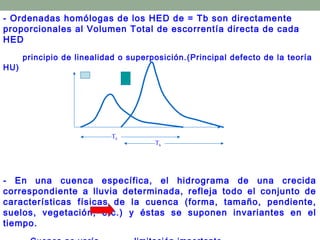
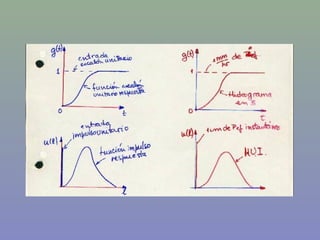
El documento trata sobre los estudios de crecidas y métodos para analizar e interpretar hidrogramas y relaciones entre precipitación y escorrentía, incluyendo el análisis de frecuencias, hidrogramas unitarios, y modelos de sistemas hidrológicos lineales y no lineales. Explica conceptos como el hidrograma unitario, función de transferencia, y métodos para modelar embalses y sistemas de escorrentía en tiempos discretos usando funciones impulso, escalón y pulso.

1. ESTUDIO DE CRECIDASESTUDIO DE CRECIDAS

2. Análisis de FrecuenciasAnálisis de Frecuencias
Análisis de Frecuencias RegionalAnálisis de Frecuencias Regional
Relaciones Precipitación-EscorrentíaRelaciones Precipitación-Escorrentía
Hidrograma UnitarioHidrograma Unitario
Fórmula RacionalFórmula Racional
Fórmula de Verni y KingFórmula de Verni y King
Q = ciAQ = ciA

3. Método del Hidrograma UnitarioMétodo del Hidrograma Unitario
Sistema LinealSistema Lineal
Modelo General de un Sistema HidrológicoModelo General de un Sistema Hidrológico
QI
dt
dS
−≡
,...),,,...,,,( 2
2
2
2
dt
Qd
dt
dQ
Q
dt
Id
dt
dI
IfS ≡
1
1
21
1
1
21
...
...
−
−
−
−
+++
++++≡
m
m
m
n
n
n
dt
Id
b
dt
dI
bIb
dt
Qd
a
dt
dQ
aQaS
...2
2
21 ++≡
dt
Qd
a
dt
dQ
a
dt
dS

4. Reemplazando en ecuación deReemplazando en ecuación de
continuidadcontinuidad
m
m
mm
m
m
n
n
nn
n
n
dt
Id
b
dt
Id
b
dt
Id
b
dt
dI
bI
Q
dt
dQ
a
dt
Qd
a
dt
Qd
a
dt
Qd
a
−−−−−
≡+++++
−
−
−
−
−
−
1
1
12
2
21
12
2
21
1
1
...
...
N(D) Q=M(D) I
)(
)(
)(
)( tI
DN
DM
tQ ≡
Función de transferencia

5. Embalse Lineal aEmbalse Lineal a11=k=k
IQ
dt
dQ
k ≡+
En sistemas Lineales:
si una solución f(Q) es multiplicada por c, al
función resultante cf(Q), es también solución
(principio de proporcionalidad)
si 2 soluciones f1(Q) y f2(Q) se suman, la
función resultante f1(Q) + f2(Q) es también
solución (superposición)

6. τ1
Entrada:
Función impulso
Salida: FunciónSalida: Función
Impulso respuestaImpulso respuesta
1
I,Q
tτ
u(t-τ)
3
2
τ2

7. Impulsos continuos son tratados como
suma de impulsos infinitesimales
Entre τ y τ+dτ entra al sistema i(τ)dτ (lluvia)
Sale Escorrentía Directa en (t-Sale Escorrentía Directa en (t-ττ)= i()= i(ττ) u(t-) u(t-ττ) dt) dt
∫ −≡
t
dtuitQ
0
)()()( τττ
Integral de convolución

8. t
Entrada:
Función Escalón
Salida: FunciónSalida: Función
Escalón respuestaEscalón respuesta
1
I,Q
t
1
I,Q
I(τ)=1 para
τ≥0
∫ −≡≡
t
dtutgtQ
0
)()()( ττ
l=t-τ dl=-dτ
∫
∫
≡
−≡
t
t
dllu
dllutg
0
0
)(
)()(

9. Entrada:
Función Pulso
Salida: FunciónSalida: Función
Pulso respuestaPulso respuesta
I,Q
t
1
∆t
I,Q
Escalón empieza
en 0 respuesta es
g(t)/Δt
Escalón empieza
en ∆t respuesta es
-g(t-∆t)/∆t
∫
∫∫
∆−
∆−
∆
≡
−
∆
≡
t
tt
ttt
dllu
t
dlludllu
t
th
)(
1
)()([
1
)(
00
∆t
I(τ)=1/∆ t para
0≤τ≤∆ t
=0 para t>∆ t

10. Hidrograma Unitario (Sherman, 1932)
HED que resulta de una Pef unitaria (1mm,
1 cm...) que se produce uniformemente
sobre la cuenca, con intensidad constante
durante una duración especificada.
Hidrograma
Unitario
Precipitación
efectiva Escorrentía
Directa
Teoría HU aplicable a sistema lineal con
cualquier entrada y salida

11. HipótesisHipótesis
- Lluvia efectiva uniforme espacialmente
Limitar a cuencas de superficie < 3000 a 5000 Km2
Si régimen de Pp es orográfico, configuración se mantiene
de una tormenta a otra y efecto poco importante
- Lluvia efectiva uniforme en el tiempo para la
duración D
Obtener HU para tormentas de corta duración (tiempo de
desfase 1/4 o 1/3 a 1/5 tc e inferior a 24 horas)
- Tb del HED es prácticamente constante para lluvias
efectivas de igual duración
Como Tb depende de método separación componentes
del HET, se acepta tolerancia ± 25% en D

12. - Ordenadas homólogas de los HED de = Tb son directamente
proporcionales al Volumen Total de escorrentía directa de cada
HED
principio de linealidad o superposición.(Principal defecto de la teoría
HU)
- En una cuenca específica, el hidrograma de una crecida
correspondiente a lluvia determinada, refleja todo el conjunto de
características físicas de la cuenca (forma, tamaño, pendiente,
suelos, vegetación, etc.) y éstas se suponen invariantes en el
tiempo.
Tb
Tb

15. Sistemas Lineales en Tiempos Discretos
Precipitación: Entrada
∫
∆
∆−
=
tm
tm
m diP
))1(
)( ττ
Caudal: Salida
m=1,2,3
Qn=Q(nΔt)
El efecto que en t=n∆ t tiene el pulso de entrada
de duración ∆ t que ocurrió en (m-1)∆ t es:
h(t-(m-1)∆ t)=h(n∆ t-(m-1)∆ t)=h(n-m+1)∆ t=
∫
∆+−
∆−
∆
=
tmn
tmn
dllu
t
)1(
)(
)(
1

16. 0
1
2
3
4
5
6
1 2 3 4 5 6
m
Pm/∆t
∫
∆
∆−
=
tm
tm
m diP
))1(
)( ττ
i(τ)=0 τ>M∆ t
m∆ t u n-m+1
n-m+1∆t
Se discretiza la
integral en n
partes
∫
∆
−∆≡
tn
n dtnuiQ
0
)()( τττ

17. ∫∫
∫∫
∆
∆−
∆
∆−
∆
∆
∆
−∆
∆
++−∆
∆
++
+−∆
∆
+−∆
∆
≡
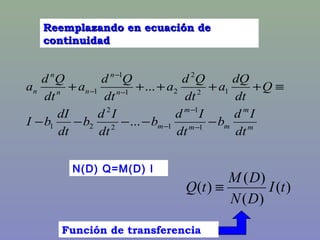
tM
tM
M
tm
tm
m
t
t
t
n
dtnu
t
P
dtnu
t
P
dtnu
t
P
dtnu
t
P
Q
)1()1(
2
2
0
1
)(...)(....
)()(
ττττ
ττττ
])1[(
)()(
)1(
)()1(
tmnhP
dllu
t
P
dtnu
t
P
m
tmn
tmn
m
tm
tm
m
∆+−≡
∆
≡−∆
∆ ∫∫
∆+−
∆−
∆
∆−
ττ
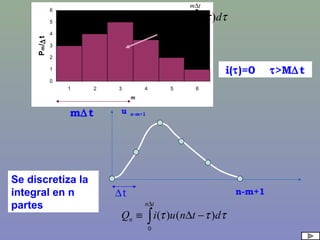
Qn=P1h[nΔt]+P2h[(n-1)Δt]+...+Pmh[(n-m+1)Δt]+...
+PMh[(n-M+1)Δt]
∑
≤
=
+−=
Mn
m
mnmn UPQ
1
1
Un-m+1=h[(n-M+1)Δt]

18. Pmh[(n-m+1)∆t]
P1h[n∆t]
∆t
Qn
n

19. HU
0
0,5
1
1,5
2
2,5
3
3,5
0 2 4 6 8 10 12n-m+1
Un-m+1
0
1
2
3
4
5
6
1 2 3 4 5 6 7 8 9 10 11 12
m
Pm
HED
0
5
10
15
20
25
30
35
0 2 4 6 8 10 12
t
Q
aP1 aP2 aP3 Q

20. Obtención HU(D) Duración de la lluvia
efectiva unitaria
Hidrogramas simples de lluvias intensas de corta
duración de distribución espacial y temporal lo mas
uniforme posible.
Determinar pluviograma medio (espacialmente) para
la cuenca
A base de índices o curvas de infiltración se
determina lluvia efectiva y duración
Se efectúa separación de las componentes del
hidrograma (F. Base y Escorrentía Directa)
Se determina Volumen de Escorrentía Directa
= Pef .
Area Pef