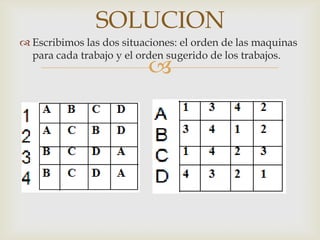
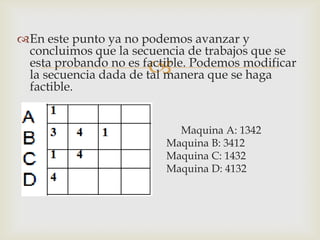
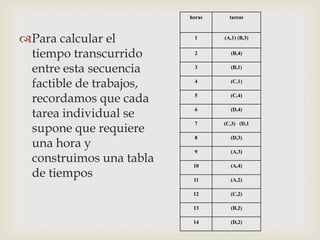
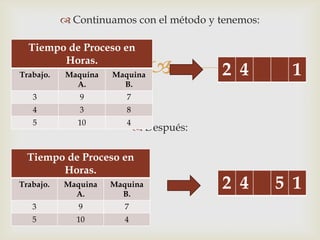
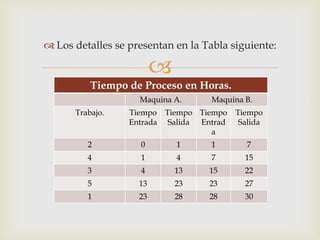
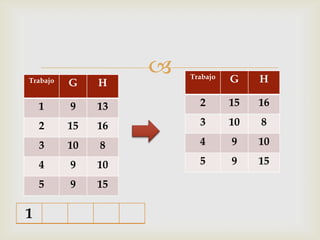
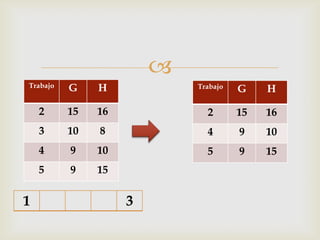
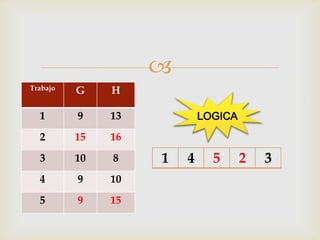
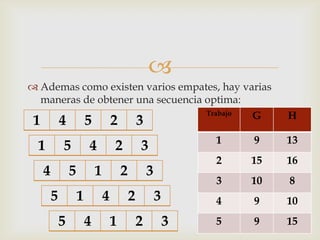
Este documento describe diferentes problemas de secuenciación de trabajos a través de múltiples máquinas. Explica cómo secuenciar n trabajos a través de 2 o 3 máquinas para minimizar el tiempo total de producción. También presenta un ejemplo numérico para ilustrar cómo aplicar el método de Johnson para secuenciar 5 trabajos a través de 2 máquinas.

1. EQUIPO 5
RODRIGUEZ ORDAZ NORMA E.
LAGUNES ELVIRA GONZALO
LOPEZ FRANCISCO CESAR A.
REYNA VAZQUEZ EDUARDO

2. En secuenciación tratamos con una situación en
donde la medida de efectividad es una función
del orden o secuencia en el que la serie de

trabajos se llevan a cabo.
Sus objetivos son:
1: Termino de productos en la fecha de entrega
2: Minimización del tiempo de producción
3: Minimización del trabajo en proceso
4: Maximización de la utilización del centro de
trabajo
5: Menor costo de producción
6: Maximización de utilidades

3. 
1. Tenemos n tareas que realizar y cada una de las
cuales necesita un proceso en algunas o en
todas las m maquinas diferentes de que se
dispone.
La efectividad para cualquier secuencia dada
de los trabajos en cada maquina puede medirse
y queremos seleccionar de las
secuencias teóricamente posibles

4. 
 A) Aquellas que son “factibles tecnológicamente”
que satisfacen las restricciones con respecto al orden
en que cada trabajo debe realizarse a través de las m
maquinas.
 B) Una o varias de las secuencias factibles
tecnológicamente que optimizan la medida de
efectividad

5. 
2. El segundo tipo de problema, tenemos un
taller con cierto numero de máquinas y una
lista de las tareas a realizar, cada vez que
una maquina complete el trabajo que esta
haciendo tenemos que decidir que tarea
debe iniciar.
Una característica de este tipo de problemas es
que la lista de trabajos a realizar cambia
conforme a nuevas ordenes.

6. PROCESO DE n TRABAJOS A
TRAVES DE m MAQUINAS

 Se tienen n (1,2,3…..n) trabajos los cuales tienen que
procesarse uno por uno en cada uno de los m
(A,B,C….) centros de maquinas y se da el orden para
procesar cada trabajo por ejemplo el trabajo 1 se
procesa en los centros de trabajo A, C y B y se dan los
tiempos en que se realizan las operaciones.

7. 
El problema consiste en encontrar una secuencia
para procesar los trabajos de manera que el
tiempo total sea el mínimo.
Se representa:
Ahí = Tiempo para el trabajo i en la maquina A
Bi= Tiempo para el trabajo i en la maquina B
T= tiempo desee la iniciación del primer trabajo
hasta completar el ultimo.

8. 
 Se dispone de soluciones satisfactorias actualmente
solo para tres casos:
1. N trabajos y 2 maquinas A y B con un orden AB
2. N trabajos y 3 maquinas A, B y C con el orden ABC
3. 2 trabajos y m maquinas con un orden prescrito que
no es necesariamente el mismo.

9. EJEMPLO 1

 Supongamos que tenemos 4 trabajos a realizar 1, 2 , 3
y 4 que deben procesarse a través de las maquinas A,
B, C y D en el siguiente orden :
 Trabajo 1: ABCD
 Trabajo 2: ACBD
 Trabajo 3: BCDA
 Trabajo 4: BCDA

10. a) Demostrar que la siguiente secuencia de
trabajos seleccionada de las secuencias

posibles no es factible:
Maquina A: 1342
Maquina B: 3412
Maquina C: 1423
Maquina D: 4321
b) Encuentre una secuencia factible de trabajos y
calcule el tiempo correspondiente T desde el
principio del primer trabajo hasta terminar el
ultimo.

11. SOLUCION
 Escribimos las dos situaciones: el orden de las maquinas
para cada trabajo y el orden sugerido de los trabajos.


12.  Al tiempo cero las tareas (A,1) y (B,3) son factibles;
indicamos se han acompletado estas dos operaciones
poniendo un circulo alrededor de cada maquina y cada
trabajo como sigue:


13.  Ahora (B,4) es factible; y continuamos circulando las
operaciones que se completan hasta que alcancemos la
siguiente situación:


14. En este punto ya no podemos avanzar y
concluimos que la secuencia de trabajos que se

esta probando no es factible. Podemos modificar
la secuencia dada de tal manera que se haga
factible.
 Maquina A: 1342
 Maquina B: 3412
 Maquina C: 1432
 Maquina D: 4132

15. horas tareas
Para calcular el 1 (A,1) (B,3)
tiempo transcurrido 2 (B,4)
entre esta secuencia 3 (B,1)
factible de trabajos, 4 (C,1)
recordamos que cada 5 (C,4)
tarea individual se 6 (D,4)
supone que requiere
7 (C,3) (D,1
una hora y
8 (D,3)
9 (A,3)
construimos una tabla 10 (A,4)
de tiempos 11 (A,2)
12 (C,2)
13 (B,2)
14 (D,2)

16. 
 El tiempo transcurrido es de 14 horas. Esto también se
puede obtener gráficamente mediante una grafica de
Gantt.
 El problema de secuencia no ha sido resuelto, todo lo
que hemos hecho es encontrar una secuencia factible y
calcular la T correspondiente ya que no se dispone de un
método matemático para encontrar la secuencia optima

17. Grafica de Gantt

1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 3 4 2 A
3 4 1 2 B
1 4 3 2 C
4 1 3 2 D

18. Procesamiento de “n” trabajos
a través de 2 maquinas.

19.  Este problema de secuenciación, para el que se dispone de una
solución, se describe como sigue:
 dos maquinas, A y B.
a) Se cuenta únicamente con
b) Cada trabajo se procesa en el orden AB.
c) Los tiempos de proceso, exactos o esperados A1, A2,…An,
B1, B2,…Bn, se conocen.

20. 
El problema es minimizar “T”, el
tiempo transcurrido desde el
principio del primer trabajo hasta
la terminación del ultimo.

21. Método:

 1.- Seleccionar el menor tiempo de proceso en la lista
A1,…An,…B1,,…Bn. Si existe empate,
seleccionar cualquiera de los dos tiempos.
2.- Si el tiempo de proceso mínimo es Ar,
hacer primero el trabajo s-esimo, para
cualquiera de las dos maquinas.

22.  3.- Quedan ahora n-1 trabajos que deben ser ordenados.
Aplicar los pasos 1 y 2 al conjunto reducido de tiempos

de proceso obtenido después de eliminar los tiempos
anteriores.
 4.- Continuar de esta manera hasta que todos los
trabajos hayan sido ordenados.
 La secuencia resultante minimiza “T”.

23. Solución:

 El tiempo mínimo de proceso es 1 hora para el
trabajo 2 en la maquina A. Por lo tanto se programa
al principio el trabajo 2:
2

24. Ejemplo:

 Se tienen 5 trabajos, cada uno de los cuales debe
pasar por las dos maquinas A y B en ese orden. Los
tiempos de proceso son los siguientes:
Tiempo de Proceso en Horas.
Trabajo. Maquina A. Maquina B.
1 5 2
2 1 6
3 9 7
4 3 8
5 10 4

25. El conjunto reducido de tiempos de

proceso ahora es:
Tiempo de Proceso en Horas.
Trabajo. Maquina A. Maquina B.
1 5 2
3 9 7
4 3 8
5 10 4

26.  El menor tiempo de proceso es de 2 y se encuentra en B,

por lo tanto se programa el trabajo al final:
2 1

27.  Continuamos con el método y tenemos:
Tiempo de Proceso en
Trabajo.
Horas.
Maquina Maquina  2 4 1
A. B.
3 9 7
4 3 8
5 10 4
 Después:
Tiempo de Proceso en
Horas.
Trabajo. Maquina
A.
Maquina
B.
2 4 5 1
3 9 7
5 10 4

28.  De manera que la secuencia optima es:

2 4 3 5 1
 Se puede calcular el tiempo transcurrido que
corresponde al ordenamiento optimo, utilizando los
tiempo individuales de proceso que se dan en el
problema.

29.  Los detalles se presentan en la Tabla siguiente:

Tiempo de Proceso en Horas.
Maquina A. Maquina B.
Trabajo. Tiempo Tiempo Tiempo Tiempo
Entrada Salida Entrad Salida
a
2 0 1 1 7
4 1 4 7 15
3 4 13 15 22
5 13 23 23 27
1 23 28 28 30

30. Conclusiones:

 Por lo tanto, el tiempo mínimo transcurrido es de 30
horas.
 Se pierden 3 horas en la Maquina B.
 Se pierden 2 horas en la Maquina A.

31. Grafica de Gantt.
0 1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1 1 1 1 1 2 3 3 3 3 3 3 3 3 3 4 4 4 5 5 5 5 5 5 5 5 5 5 - - - - - - A
1
3
1
4
1
5

1
6
1
7
1
8
1
9
2
0
2
1
2
2
2
3
2
4
2
5
2
6
2
7
2
8
2
9
3
0
3
1
3
2
3
3
3
4
- - - - - 1 1 2 2 2 2 2 2 - - 3 3 3 3 3 3 3 4 4 4 4 4 4 4 45 5 5 5 B
Resultados antes de aplicar la regla de
Johnson.
(6 horas perdidas en A y 7 en B, 34 horas
totales)
0 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
2 4 4 4 3 3 3 3 3 3 3 3 3 5 5 5 5 5 5 5 5 5 5 1 1 1 1 1 - - A
- 2 2 2 2 2 2 4 4 4 4 4 4 4 4 3 3 3 3 3 3 3 - 5 5 5 5 - 1 1 B
Resultados después de aplicar la regla de
Johnson.
(2 horas perdidas en A y 3 en B, 30 horas
totales)

32. Procesamiento de “n” trabajos
a través de 3 maquinas.

33. OBJETIVOS DE LA SECUENCIACIÓN DE
TRABAJOS:

 1: Termino de productos en la fecha de entrega
 2: Minimización del tiempo de producción
 3: Minimización del trabajo en proceso
 4: Maximización de la utilización del centro de
trabajo
 5: Menor costo de producción
 6: Maximización de utilidades

34. PROGRAMACION DE N PEDIDOS EN
TRE MAQUINAS

 No se dispone actualmente de una solución para el
problema general de la secuencia de n trabajos, 3
maquinas A, B y C orden prescrito ABC para cada
trabajo, y el mismo orden para las 3 maquinas.
 Sin embargo, el metodo para secuenciar n trabajos e
2 maquinas, puede extenderse para cubrir los casos
especiales en donde una, o las dos condiciones
siguientes, se cumplen:

35. REGLA DE JOHNSON AMPLIADA.

 a) El tiempo minimo de proceso para la maquina A
es al menos tan grande como el maximo tiempo de
proceso para la maquina B.
 b) El tiempo minimo de proceso para la maquina C
es al menos tan grande como el maximo tiempo de
proceso para la maquina B

36. 
 El metodo que se da aquí, consiste en reemplazar el
problema, por uno equivalente que requiere n
trabajos y dos maquinas. Denotamos las maquinas
ficticias como G y H, y definimos los tiempos
correspondientes de proceso Gi y Hi, mediante:
Gi = Ai + Bi
Hi = Bi + Ci

37. 
 Resolvemos el nuevo problema, con orden prescrito
GH, mediante el metodo de la sección anterior. La
secuencia la óptima resultante será tambien óptima
para el problema original.

38. Ejemplo
 de los cuales debe
 Tenemos 5 trabajos, cada uno
pasar por las maquinas A, B y C en el orden prescrito
ABC. Los tiempos de proceso son:
Trabajo A B C
1 4 5 8
2 9 6 10
3 8 2 6
4 6 3 7
5 5 4 11
Determine una secuencia para los 5 trabajos que minimice el
tiempo transcurrido T

39. Solución

Trabajo A B C Minimo de Ai = 4
Maximo de Bi = 6
1 4 5 8
Minimo de Ci = 6
2 9 6 10
Considerando la regla de
3 8 2 6 Johnson tenemos:
4 6 3 7 Max Bi ≤ Min Ci
× Min Ai ≥ Max Bi
A lo que el problema
5 5 4 11
equivalente se convierte en:
 Min Ci ≥ Max Bi

40. Trabajo A B C
 Trabajo G H
1 4 5 8 1 9 13
2 9 6 10 2 15 16
3 8 2 6 3 10 8
4 6 3 7 4 9 10
5 5 4 11 5 9 15
Gi = Ai + Bi
Hi = Bi + Ci

41. Trabajo
 Trabajo G H
G H
1 9 13 2 15 16
2 15 16 3 10 8
3 10 8 4 9 10
4 9 10 5 9 15
5 9 15
1

42. 
Trabajo G H Trabajo G H
2 15 16 2 15 16
3 10 8 4 9 10
4 9 10 5 9 15
5 9 15
1 3

43. 
Trabajo G H
Trabajo G H
2 15 16
4 9 10 2 15 16
5 9 15 5 9 15
1 4 3

44. 
Trabajo G H Trabajo G H
2 15 16 5 9 15
5 9 15
1 4 2 3 1 4 5 2 3
 ¿Por qué nos quedo así?

45. 
Trabajo G H
1 9 13 LOGICA
2 15 16
3 10 8 1 4 5 2 3
4 9 10
5 9 15

46. 
 Ademas como existen varios empates, hay varias
maneras de obtener una secuencia optima:
Trabajo G H
1 4 5 2 3
1 9 13
1 5 4 2 3
2 15 16
4 5 1 2 3
3 10 8
5 1 4 2 3 4 9 10
5 4 1 2 3 5 9 15

47. 
 Cualquiera de la secuencias anteriores pueden usarse
para ordenar los trabajos en las maquinas A, B y C;
todas dan por resultados un tiempo minimo
transcurrido de 51 horas.

48. Grafica de Gantt
