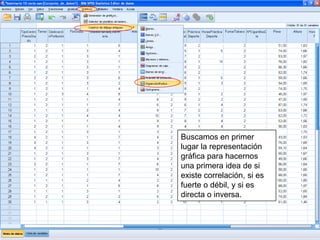
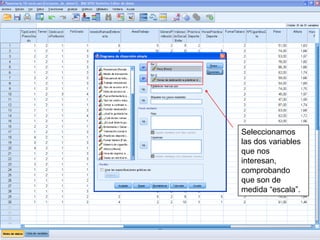
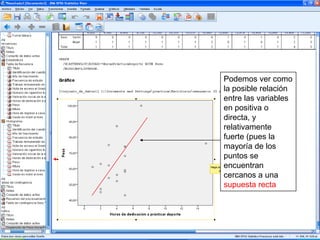
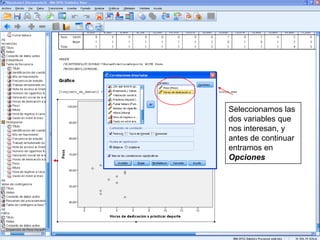
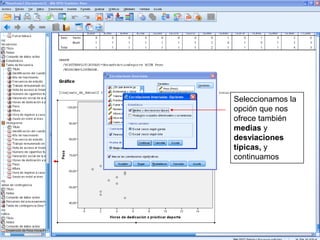
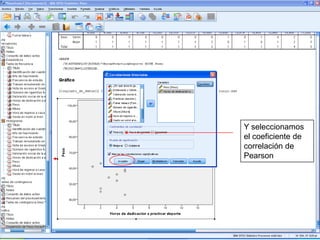
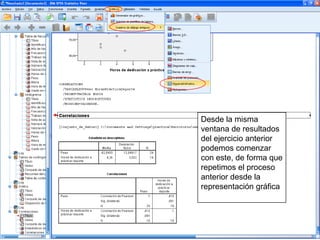
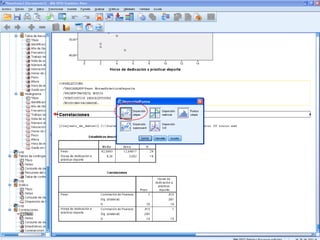
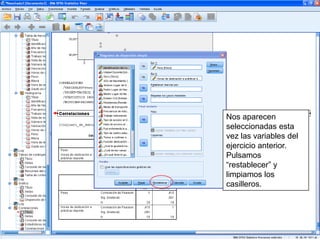
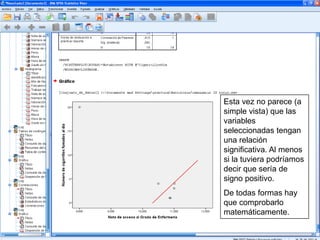
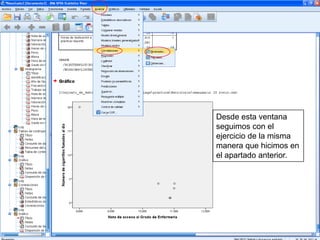
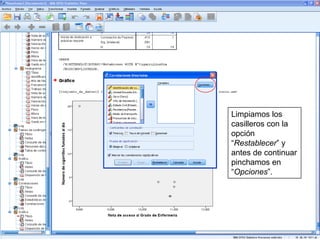
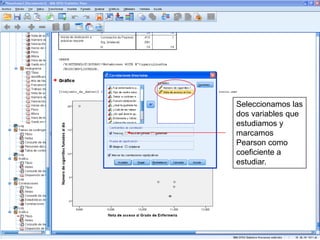
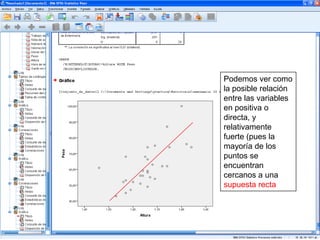
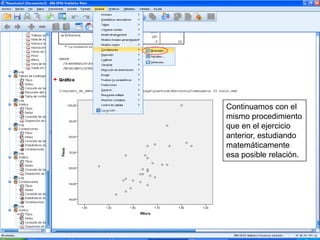
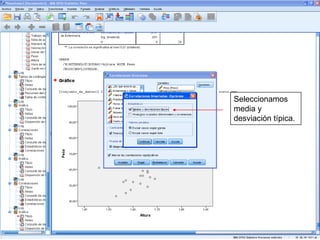
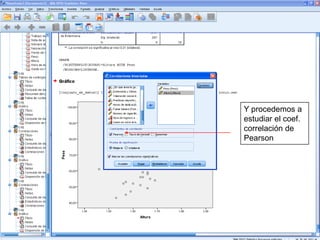
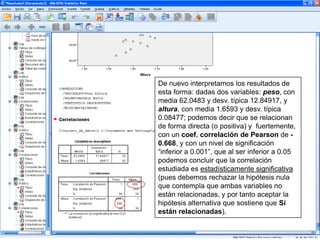
El documento describe un seminario sobre correlación que estudia la relación entre diferentes variables mediante el coeficiente de correlación de Pearson. Se analizan la correlación entre peso y horas de deporte, número de cigarrillos y nota de acceso, y peso y altura. Los resultados muestran una correlación positiva moderada entre peso y deporte, una correlación negativa muy fuerte entre cigarrillos y nota, y una correlación positiva fuerte entre peso y altura.

1. SEMINARIO X
CORRELACIÓN
1. Utilizando nuestra base de datos, comprueba la
correlación entre la variable “peso” y la variable
“horas dedicadas al deporte”. Comenta los
resultados.

2. Descargamos y ejecutamos el
archivo en cuestión.
Comprobamos la pestaña
“Vista de variables” ….

3. …y la pestaña “Vista de datos”

4. Pulsamos en el botón
“Etiquetas de valor” para
pasar todos los datos a
numéricos

5. Buscamos en primer
lugar la representación
gráfica para hacernos
una primera idea de si
existe correlación, si es
fuerte o débil, y si es
directa o inversa.

7. Seleccionamos
las dos variables
que nos
interesan,
comprobando
que son de
medida “escala”.

8. Podemos ver como
la posible relación
entre las variables
en positiva o
directa, y
relativamente
fuerte (pues la
mayoría de los
puntos se
encuentran
cercanos a una
supuesta recta

9. Pasamos ahora a
comprobarlo
matemáticamente,
para lo cual
procedemos a
estudiar el
coeficiente de
correlación de
Pearson

10. Seleccionamos las
dos variables que
nos interesan, y
antes de continuar
entramos en
Opciones

11. Seleccionamos la
opción que nos
ofrece también
medias y
desviaciones
típicas, y
continuamos

12. Y seleccionamos
el coeficiente de
correlación de
Pearson

13. El programa nos ofrece los
resultados, y los interpretamos de la
siguiente manera: dadas dos
variables: peso, con media 62.0483 y
desv. típica 12.84917, y horas
dedicadas a deporte, con media
4.26 y desv. típica 3.052; podemos
decir que se relacionan de forma
positiva y con una fuerza moderada,
con un coef. correlación de
Pearson de 0.41, pero cuyo nivel de
significación es de 0.091, que al ser
superior a 0.05 podemos concluir que
la correlación estudiada no es
estadísticamente significativa (pues
debemos aceptar la hipótesis nula
que contempla que ambas variables
no están relacionadas).

14. SEMINARIO X
CORRELACIÓN
2. Estudiar el coeficiente de correlación de
Pearson para las variables “nº de cigarrillos
fumados al día” y “nota de acceso”. Comenta
los resultados.

15. Desde la misma
ventana de resultados
del ejercicio anterior
podemos comenzar
con este, de forma que
repetimos el proceso
anterior desde la
representación gráfica

17. Nos aparecen
seleccionadas esta
vez las variables del
ejercicio anterior.
Pulsamos
“restablecer” y
limpiamos los
casilleros.

18. Introducimos las dos
variables que nos
indica el apartado.

19. Esta vez no parece (a
simple vista) que las
variables
seleccionadas tengan
una relación
significativa. Al menos
si la tuviera podríamos
decir que sería de
signo positivo.
De todas formas hay
que comprobarlo
matemáticamente.

20. Desde esta ventana
seguimos con el
ejercicio de la misma
manera que hicimos en
el apartado anterior.

21. Limpiamos los
casilleros con la
opción
“Restablecer” y
antes de continuar
pinchamos en
“Opciones”.

22. Indicamos que
también queremos
en los resultados la
media y la
desviación típica
de las variables
estudiadas, y
continuamos.

23. Seleccionamos las
dos variables que
estudiamos y
marcamos
Pearson como
coeficiente a
estudiar.

24. De nuevo interpretamos los
resultados de esta forma: dadas dos
variables: nº de cigarrillos fumados
al día, con media 5.50 y desv. típica
7.232, y notas de acceso, con media
10.64307 y desv. típica 0.982116;
podemos decir que se relacionan de
forma inversa y muy fuertemente, con
un coef. correlación de Pearson de
-0.976, y con un nivel de significación
de 0.001, que al ser inferior a 0.05
podemos concluir que la correlación
estudiada es estadísticamente
significativa (pues debemos rechazar
la hipótesis nula que contempla que
ambas variables no están
relacionadas, y por tanto aceptar la
hipótesis alternativa que sostiene que
Sí están relacionadas).

25. SEMINARIO X
CORRELACIÓN
3. Estudiar el coeficiente de correlación de
Pearson para las variables “peso” y “altura”.
Comenta los resultados.

26. Se procede de forma
idéntica al apartado
anterior…

28. …pero seleccionando
las variables “peso” y
“altura”.

29. Podemos ver como
la posible relación
entre las variables
en positiva o
directa, y
relativamente
fuerte (pues la
mayoría de los
puntos se
encuentran
cercanos a una
supuesta recta

30. Continuamos con el
mismo procedimiento
que en el ejercicio
anterior, estudiando
matemáticamente
esa posible relación.

31. Seleccionamos
las variables y
vamos a
“Opciones”

32. Seleccionamos
media y
desviación típica.

33. Y procedemos a
estudiar el coef.
correlación de
Pearson

34. De nuevo interpretamos los resultados de
esta forma: dadas dos variables: peso, con
media 62.0483 y desv. típica 12.84917, y
altura, con media 1.6593 y desv. típica
0.08477; podemos decir que se relacionan
de forma directa (o positiva) y fuertemente,
con un coef. correlación de Pearson de -
0.668, y con un nivel de significación
“inferior a 0.001”, que al ser inferior a 0.05
podemos concluir que la correlación
estudiada es estadísticamente significativa
(pues debemos rechazar la hipótesis nula
que contempla que ambas variables no
están relacionadas, y por tanto aceptar la
hipótesis alternativa que sostiene que Sí
están relacionadas).

35. SEMINARIO X
CORRELACIÓN
4. Mostrar la gráfica de una de las correlaciones.
En cada unos de los tres casos anteriores se ha
iniciado el estudio de la correlación con la gráfica
correspondiente, la cual nos ha ayudado a aproximar
qué tipo de correlación mantenían las variables.