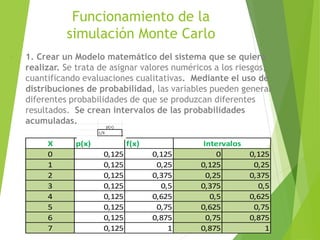
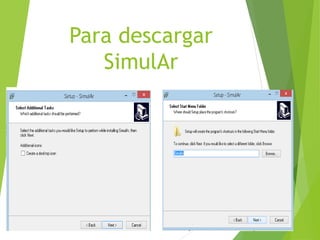
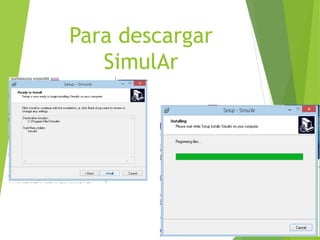
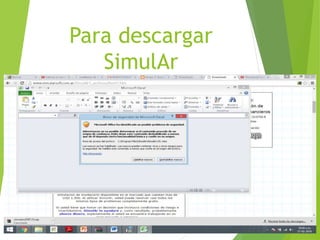
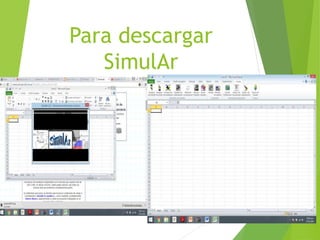
La simulación Monte Carlo es una técnica matemática que permite considerar el riesgo en análisis cuantitativos y tomas de decisiones. Muestra posibles resultados y sus probabilidades de acuerdo a medidas tomadas. La empresa Tortas y Café quiere usar esta técnica para decidir entre 8 sabores de tortas. El proceso implica asignar distribuciones de probabilidad a variables, generar muestras aleatorias repetidamente, y analizar los resultados para determinar el sabor más probable de obtener mayores ganancias.

1. En qué consiste la simulación
Monte Carlo
 La simulación Monte Carlo es una técnica matemática
computarizada que permite tener en cuenta el riesgo en
análisis cuantitativos y tomas de decisiones.
 Esta técnica ofrece a la persona responsable de tomar las
decisiones una serie de posibles resultados, así como la
probabilidad de que se produzcan según las medidas tomadas.
Muestra las posibilidades extremas —los resultados de tomar la
medida más arriesgada y la más conservadora— así como todas
las posibles consecuencias de las decisiones intermedias

2. Funcionamiento de la
simulación Monte Carlo
 Caso Ejemplo
 Planteamiento del Problema:
 Tortas y Café.; es una empresa que está creciendo en el
mercado de tortas y exquisiteces y está estudiando la
posibilidad de invertir en una línea de tortas con
combinaciones y sabores diferentes y quieren escoger entre 8
posibles sabores, el que les proporcione mejores ganancias al
cabo de 3 meses. Los sabores que tienen en mente para
invertir son: Selva negra con chocolate blanco, cereza con
chocolate, frutas con arequipe, naranja con almendras, crema
pastelera con frambuesas, coco con pasas, plátano maduro
con miel de abeja y frutos secos con crema pastelera.
 0= Selva negra con chocolate blanco 1= cereza con chocolate
 2= frutas con arequipe 3= naranja con almendras
 4= crema pastelera con frambuesas 5= coco con pasas
 6= plátano maduro con miel de abeja 7= frutos secos con
crema pastelera

3. Funcionamiento de la
simulación Monte Carlo
 1. Crear un Modelo matemático del sistema que se quiere
realizar. Se trata de asignar valores numéricos a los riesgos,
cuantificando evaluaciones cualitativas. Mediante el uso de
distribuciones de probabilidad, las variables pueden generar
diferentes probabilidades de que se produzcan diferentes
resultados. Se crean intervalos de las probabilidades
acumuladas.
X p(x) f(x)
0 0,125 0,125 0 0,125
1 0,125 0,25 0,125 0,25
2 0,125 0,375 0,25 0,375
3 0,125 0,5 0,375 0,5
4 0,125 0,625 0,5 0,625
5 0,125 0,75 0,625 0,75
6 0,125 0,875 0,75 0,875
7 0,125 1 0,875 1
Intervalos

4. Funcionamiento de la
simulación Monte Carlo
 2.Se lleva a cabo un experimento consistente en generar
muestras aleatorias para las variables. En Excel se le da clip
sobre una celda y coloca =ALEATORIO( Y PRESIONA ENTER.
Luego en otra celda coloca BUSCAR(introduce las variables y los
intervalos. Ejem: D15;$F$5:$G$12;$C$5:$C$12) Y PRESIONA ENTER.
I
X p(x) f(x)
0 0,125 0,125 0 0,125
1 0,125 0,25 0,125 0,25
2 0,125 0,375 0,25 0,375
3 0,125 0,5 0,375 0,5
4 0,125 0,625 0,5 0,625
5 0,125 0,75 0,625 0,75
6 0,125 0,875 0,75 0,875
7 0,125 1 0,875 1
Intervalos

5. Funcionamiento de la
simulación Monte Carlo
 3. Tras repetir n veces este experimento, dispondremos de
"n" observaciones sobre el comportamiento del sistema.
Dependiendo del número de incertidumbres y de los rangos
especificados, para completar una simulación Monte Carlo
puede ser necesario realizar miles o decenas de miles de
recálculos.
0,857899248 6
0,594525273 4
0,127598207 1
0,12751385 1
0,580032038 4
0,447620264 3
0,477003005 3
0,986510216 7
0,416466072 3
0,734231347 5
0,277112542 2
0,425216846 3
0,711880993 5
0,088061202 0
0,096049652 0
0,444069769 3
0,238180761 1

6. Funcionamiento de la
simulación Monte Carlo
4.Nuestro Análisis, será tanto más preciso cuanto Mayor sea el
número n de experimentos que llevemos a cabo Importancia del
método Montecarlo.
La simulación Monte Carlo realiza esta operación cientos o miles de
veces, y el resultado es una distribución de probabilidad de posibles
resultados. De esta forma, la simulación Monte Carlo proporciona
una visión mucho más completa de lo que puede suceder. Indica no
sólo lo que puede suceder, sino la probabilidad de que suceda.
0=2veces
1=3veces
2= 1 vez
3=5veces
4=2veces
5=2veces
6=2veces
7=1vez En 3 meses se venderá más la n° 3= naranja con almendras

7. Las distribuciones de
probabilidad
Las distribuciones de probabilidad son una forma mucho más
realista de describir la incertidumbre en las variables de un
análisis de riesgo. Las distribuciones de probabilidad más
comunes son:
 Normal: Los valores intermedios cercanos a la media tienen
mayor probabilidad de producirse.
 Lognormal –Se utiliza para representar valores que no bajan
por debajo del cero, pero tienen un potencial positivo
ilimitado
 Uniforme – Todos los valores tienen las mismas probabilidades
de producirse; el usuario sólo tiene que definir el mínimo y el
máximo.
 Triangular – El usuario define los valores mínimo, más probable
y máximo. Los valores situados alrededor del valor más
probable tienen más probabilidades de producirse.

8. Las distribuciones de
probabilidad
Las distribuciones de probabilidad son una forma mucho más
realista de describir la incertidumbre en las variables de un
análisis de riesgo. Las distribuciones de probabilidad más
comunes son:
 Normal: Los valores intermedios cercanos a la media tienen
mayor probabilidad de producirse.
 Lognormal –Se utiliza para representar valores que no bajan
por debajo del cero, pero tienen un potencial positivo
ilimitado
 Uniforme – Todos los valores tienen las mismas probabilidades
de producirse; el usuario sólo tiene que definir el mínimo y el
máximo.
 Triangular – El usuario define los valores mínimo, más probable
y máximo. Los valores situados alrededor del valor más
probable tienen más probabilidades de producirse.

9. Las distribuciones de
probabilidad
 PERT – El usuario define los valores mínimo, los más
probables y máximo. Los valores situados alrededor del
más probable tienen más probabilidades de
producirse. Sin embargo, los valores situados entre el más
probable y los extremos tienen más probabilidades de
producirse; es decir, los extremos no tienen tanto peso.
 Discreta – El usuario define los valores específicos que
pueden ocurrir y la probabilidad de cada uno.

10. Ventajas de la Simulación
Monte Carlo
 Resultados probabilísticos. Los resultados muestran no sólo lo
que puede suceder, sino lo probable que es un resultado.
 Resultados gráficos. es fácil crear gráficos de diferentes
resultados.
 Análisis de sensibilidad. resulta más fácil ver qué variables
introducidas tienen mayor influencia sobre los resultados
finales.
 Análisis de escenario. los analistas pueden ver exactamente
los valores que tienen cada variable cuando se producen
ciertos resultados.

11. software SimulAr
 SimulAr, es un software de simulación Monte Carlo
desarrollado en Argentina y diseñado para el análisis y
evaluación de negocios y toma de decisiones que involucran
riesgo. SimulAr es un programa diseñado como complemento
de Microsoft Excel (Add-in) y se caracteriza por su simplicidad
y flexibilidad permitiéndole al usuario manejarse dentro de un
entorno ya conocido.
SimulAr consiste en asignar distribuciones de frecuencias a las
variables del modelo que tienen riesgo y, posteriormente generar
números aleatorios acordes a esas distribuciones “simulando” el
comportamiento que se considera que tendrán en el futuro. De
esta manera es posible darle más realismo al modelo obteniendo
resultados más confiables a la hora de tomar una decisión.

12. Para descargar
SimulAr

13. Para descargar
SimulAr

14. Para descargar
SimulAr

15. Para descargar
SimulAr

16. Para descargar
SimulAr

17. Para descargar
SimulAr

18. Para descargar
SimulAr

19. Para descargar
SimulAr

20. Para descargar
SimulAr

21. Para descargar
SimulAr

22. Para descargar
SimulAr

23. Para descargar
SimulAr

24. PASOS PARA SIMULAR
EN MONTECARLO
USANDO EL SOFWARE
SimulAr (ejemplo)

25. Caso Practico
El siguiente ejercicio trata de la empresa confecciones de
ropa donde esta tiene 2 proyectos para invertir el
primero es ropa de niñas y el segundo ropa para niños,
cada uno de estos cuenta con 6 posibilidades al azar.
A continuación pasos para realizar el estudio de simulación
de nuestros siguiente ejemplo.

26. 1. Definición del sistema bajo estudio
El objetivo del ejercicio es ver cual de los proyecto es mas
factible para la empresa confecciones de ropa.
2. Definir las variables:
El ejercicio cuenta con los siguientes elementos:
 Ropa para niñas.
 Ropa para niños
 Suma

27. 3. Recolección de datos:
 Ropa para niñas que el numero será aleatorio según dé la
distribución de probabilidad seleccionada.
 Ropa para niños que será igual aleatorio y según dé la
distribución de probabilidad seleccionada.
 Y la suma que se hará de los dos proyectos anteriores.
4.Generación del modelo de simulación preliminar.
La información ya recaudada debemos traducirla al lenguaje
del programa que vamos a utilizar para la simulación es
decir que en este caso el lenguaje seria los términos que
emplea el programa SimulAr para definir el modelo.
5. Verificación de modelo
6. Validez del modelo
7. Experimentación
8. Interpretación