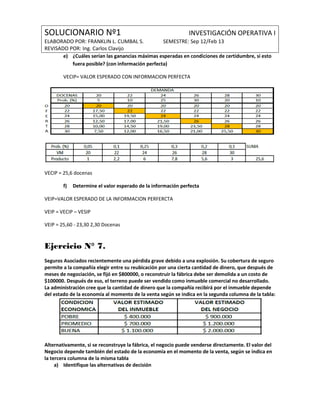
Este documento presenta la solución a varios ejercicios de un capítulo de Investigación Operativa I. Incluye problemas sobre maximización de ganancias, determinación de puntos de equilibrio, análisis de decisiones bajo incertidumbre y uso de criterios como el de Bayes. El documento proporciona detalles sobre cada ejercicio resuelto, como funciones, tablas, gráficos y cálculos algebraicos.