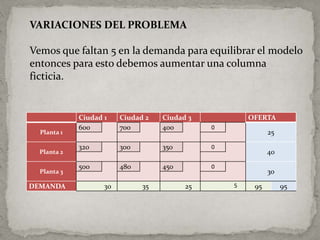
Este documento presenta un problema de transporte que involucra el suministro de electricidad de 3 plantas a 3 ciudades. Se formula un modelo matemático para minimizar los costos de transporte sujeto a restricciones de oferta y demanda. Se determina una solución factible inicial usando el método noreste y se concluye que la planta 1 abastecerá a la ciudad 1, la planta 2 abastecerá a las ciudades 1 y 2, y la planta 3 abastecerá a las ciudades 3 y 4, a un costo total de $

1. PROBLEMA DE TRANSPORTEEJERCICIO RESUELTO CON ELMÉTODO NORESTE

2. Tres plantas de energía eléctica con capacidades de 25, 40 y 30 millones dekw/hora, proporciona electricidad a tres ciudades. La demanda máximaen las tres ciudades se calcula en 30, 35 y 25 millones de kw/hora. En latabla siguiente se proporciona el precio por millón de kw/hora en las tresciudades:a. Elabore la red de transporte para este problemab. Formule el modelo matemático para el problemac. Determine la solución factible inicial para el problemad. Determine qué plantas debe abastecer de energía a qué ciudades y el costo del suministro

3. DESARROLLOa. Elabore la red de transporte para este problemaSUMINISTRODEMANDACOSTO600PLANTA 1CUIDAD 13025700400320PLANTA 2CUIDAD 23004035350480500PLANTA 3CUIDAD 34503025

4. b. Formule el modelo matemático para el problema EL PRECIO POR MILLÓN DE KW/HORA DESDE LA PLANTA 1600x11+700 x12 + 400 x13EL PRECIO POR MILLÓN DE KW/HORA DESDE LA PLANTA 2320x21+300 x22 + 350 x23EL PRECIO POR MILLÓN DE KW/HORA DESDE LA PLAMTA3500x31+480 x32 + 450x33

5. RESTRICCIONES SUMINISTROx11+ x12 + x13 ≤ 25 suministro de ciudad 1x21+ x22 + x23≤ 40 suministro de ciudad 2x31+ x32 + x33≤ 30 suministro de ciudad 3RESTRICCIONES DEMANDAx11+ x21 + x31 ≤ 30 demanda de ciudad 1x12+ x22 + x32≤ 35 demanda de ciudad 2x13+ x23 + x33≤ 25 demanda de ciudad 3

6. FUNCIÓN OBJETIVOMin600x11+700 x12 + 400 x13 + 320x21+300 x22 + 350 x23+ 500x31+480 x32 + 450x33S.ax11+ x12 + x13 ≤ 25x21+ x22 + x23≤ 40x31+ x32 + x33≤ 30x11+ x21 + x31 ≤ 30x12+ x22 + x32≤ 35x13+ x23 + x33≤ 25 xji≥ para i = 1,2,3 y j = 1,2,3

7. c. Determine la solución factible inicialPara el problema se determinara el valor factible con el método rincón noresteComo podemos ver la demanda y la oferta no tienen el mismo costo por lo tanto la modelo no está esta balanceada.

8. VARIACIONES DEL PROBLEMAVemos que faltan 5 en la demanda para equilibrar el modelo entonces para esto debemos aumentar una columna ficticia.

9. Se procede a ingresar los valores de acuerdo con el método noresteNOTA: Para recordar como se realiza el método noreste mirar el video DEMOSTRACIÓN DEL MÉTODO NORESTE PARA UN MODELO NO EQUILIBRADO de esta misma pagina Si estas mirando esto por slideshare ingresar a la siguiente dirección http://sites.google.com/site/sofilutm/informatica/investigacion-de-operaciones

10. d. Determine qué plantas debe abastecer de energía a qué ciudades y el costo del suministro.La panta 1 deberá abastecer 25 millones de kw/hora a la ciudad 1 con un costo de 600La panta 2 deberá abastecer 5 millones de kw/hora a la ciudad 1 con un costo 320La panta 2 deberá abastecer 35 millones de kw/hora a la ciudad 2 con un costo de 300La panta 3 deberá abastecer 25 millones de kw/hora a la ciudad 3 con un costo de 450La panta 3 deberá abastecer 5 millones de kw/hora a la ciudad 4 con un costo de 0

11. Determinar si esta solución es degenerada o no1. Contamos el número de asignaciones Son 5 asignaciones2. Comprobar el número máximo posible m+n-1= 3+4-1= 6En conclusión esta solución es degenerada