Este documento resume varios conceptos clave relacionados con el análisis financiero, incluidos los factores de pago único, valor presente, recuperación de capital, factores de gradiente aritmético, e interpolación. Explica las fórmulas y notación estándar para estos conceptos y proporciona ejemplos numéricos para ilustrar cómo aplicarlos para calcular valores futuros y tasas de interés desconocidas.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN
INSTITUTO UNIVERSITARIO POLITÉCNICO
SANTIAGO MARIÑO
CATEGRA : ING. ECONÓMICA
Factores que Afectan el Dinero
ALUMNO :
KENEDY GUTIERREZ
23.468.439
Barcelona 30/01/2019

2. Introducción
Por medio del presente informe se le dará a conocer unos de los temas mas
importante en el área del financiamiento como son el pago único ,Factores de
Valor Presente y recuperación de capital, Factor de Gradiente Aritmético P/G y A/G
por otra parte podemos mencionar la interpolación la cual es un proceso
matemático para calcular el valor de una variable dependiente en base a valores
conocidos de las variables dependientes vinculadas, donde la variable
dependiente es una función de una variable independiente. Se utiliza para
determinar las tasas de interés por un período de tiempo que no se publican o
no están disponibles. En este caso, la tasa de interés es la variable
dependiente, y la longitud de tiempo es la variable independiente. Para
interpolar una tasa de interés, tendrás la tasa de interés de un período de
tiempo más corto y la de un período de tiempo más largo.

3. FACTORES DE PAGO UNICO
 FACTORES DE PAGO UNICO
 La relación de pago único se debe a que dadas unas variables en el tiempo,
específicamente interés (i) y número de periodos (n), una persona recibe capital
una sola vez, realizando un solo pago durante el periodo determinado
posteriormente. A continuación se presentan los significados de los símbolos a
utilizaren las fórmulas financieras de pagos únicos:,
 P: Valor presente de algo que se recibe o que se paga en el momento cero.
 F: Valor futuro de algo que se recibirá o se pagará al final del periodo evaluado.
 n: Número de períodos (meses, trimestres, años, entre otros) transcurridos
entre lo que se recibe y lo que se paga, o lo contrario; es decir, período de
tiempo necesario para realizar una transacción. Es de anotar, que n se puede o
no presentar en forma continua según la situación que se evaluando.
 i : Tasa de interés reconocida por período, ya sea sobre la inversión o la
financiación obtenida; el interés que se considera en las relaciones de pago
único es compuesto.

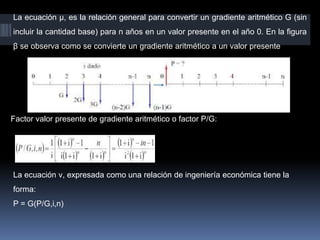
4. Factores de Valor Presente y recuperación de capital
Capitalización es el valor de mercado de la empresa, esto es, la cotización de cada acción
multiplicada por el número de acciones. El aumento de la capitalización en una año es la
capitalización al final de dicho año menos la capitalización al final del año anterior.
Factor de fondo de amortización y cantidad compuesta.
Factor de cantidad compuesta pago único (FCCPU) o factor F/P:
F = P (1+i)n
Factor de valor presente, pago único (FVPPU) o factor P/F:
P = F [1 / (1+i)n]
Factor del valor presente, serie uniforme (FVP-SU) o factor P/A:
P = A [(1+i)n-1 / i(1+i)n]
Factor de recuperación del capital (FRC) o factor A/P:
A = P [i(1+i)n / (1+i)n-1]
Factor del fondo de amortización (FA) o factor A/F:
A = F [i / (1+i)n-1]
Factor de cantidad compuesta, serie uniforme (FCCSU) o factor F/A:
F = A [(1+i)n-1 / i]

5. Notación estándar de los factores:
Para identificar factores es más sencillo utilizar la notación estándar de los nombres
de los factores y ésta será utilizada en lo sucesivo:
Nombre del factor notación estándar:
Valor presente, pago único
(P/F,i,n)
Cantidad compuesta, pago único
(F/P,i,n)
Valor presente, serie uniforme
(P/A,i,n)
.
Recuperación del capital
(A/P,i,n)
Fondo de amortización
(A/F,i,n)
Cantidad compuesta, serie uniforme
(F/A,i,n)
La notación anterior es útil para buscar los valores de los factores involucrados los
cuales se establecen en las tablas correspondientes

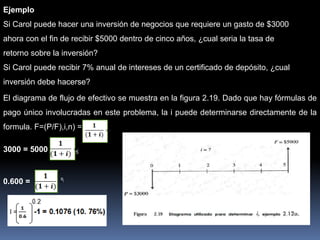
6. Ejemplo: 1
(P/A,5%,10) es el factor utilizado en el cálculo de un valor presente, dado el
valor de una anualidad, con una tasa de interés del 5% y un valor de 10
periodos de capitalización. Este factor, en las tablas correspondientes es igual a
7.7217
Si utilizamos la fórmula para calcular el valor de este factor (P/A), tenemos:
(P/A,5%,10) = [(1+i)n-1 / i(1+i)n]
= (1.05)10-1 / 0.05(1.05)10
= 7.7217

7. Un contratista independiente realizó una
auditoria de algunos registros viejos y
encontró que el costo de los suministros de
oficinas variaban como se muestra en la
siguiente tabla:
Año 0 $600
Año 1 $175
Año 2 $300
Año 3 $135
Año 4 $250
Año 5 $400
F = 600(F/P,5%,10) +
300(F/P,5%,8)+400(F/P,5%,5) F=?
F = $1931.11
0 1 2 3 4 5 6 7 8 9 10
300
400
600
Otra forma de solucionarlo
P = 600+300(P/F,5%,2)+400(P/F,5%,5) =
$1185.50
F = $1185.50(F/P,5%,10) =
1185.50(1.6289) = $1931.06
Si el contratista deseaba conocer el valor
equivalente de las 3 sumas más grandes
solamente, ¿Cuál será ese total a una tasa
de interés del 5%?
Ejemplo:2

8. INTERPOLACIÓN ENTABLAS DE INTERÉS
El primer paso en la interpolación lineal es establecer los factores conocidos
(valores 1y 2) y desconocidos, como se muestra en la tabla 2.5. Se escribe
entonces una ecuación de razones y se resuelve para c, de la siguiente manera:
O
donde a, b, c y d representan las diferencias entre los números que se
muestran en las tablas de interés. El valor de c de la ecuación (2.20) se
suma o se resta del valor 1, dependiendo de si el valor del factor está
aumentando o disminuyendo, respectivamente. Los siguientes ejemplos
ilustran el procedimiento recién descrito.
ecuación (2.20)
Utilice la regla de L´ Hospital para modificar la ecuación (2.18)
Sustituya E = i para obtener la ecuación (2.19) Los cálculos
del flujo efectivo que contienen series geométricas se
analizan en la sección 2.10.
o

9. Gradiente Aritmético
Gradiente aritmético (G) es una serie de flujos de efectivo que aumenta o disminuye en
una cantidad constante.
El flujo de efectivo al final del año 1 no forma parte de la serie del gradiente, sino que es
una cantidad base.
El flujo efectivo en el año n se calcula como:
CFn = cantidad base + (n-1) G
Si se ignora la cantidad base, se construye un diagrama de flujo de efectivo
generalizado de gradiente aritmético (gradiente convencional).
Factores de gradiente aritmético (P/G Y A/G)

10. Factor de Gradiente Aritmético P/G
En la figura α el valor presente en año 0 sólo del gradiente es igual a suma de
valores presentes de pagos individuales, donde cada valor se considera como una
unidad futura:
P=G(P/F,i,2)+2G(P/F,1,3)+3G(P/F,i,4)+…..+[(n-2)G](P/F,i,n-1)+[(n-1)G](P/F,i,n)
Factorizando G y aplicando la fórmula P/F:
Al multiplicar ambos lados de θ por
(1+i)1 se obtiene:
Restar la ecuación θ de la ecuación κ y
simplificar:
La expresión entre corchetes (de la
izquierda) es igual a la ecuación β,
donde se derivó P/A. Sustituir la
forma cerrada de P/A de la ecuación δ
en la ecuación λ y despejar P:

11. La ecuación μ, es la relación general para convertir un gradiente aritmético G (sin
incluir la cantidad base) para n años en un valor presente en el año 0. En la figura
β se observa como se convierte un gradiente aritmético a un valor presente
Factor valor presente de gradiente aritmético o factor P/G:
La ecuación ν, expresada como una relación de ingeniería económica tiene la
forma:
P = G(P/G,i,n)

12. Factor de Gradiente Aritmético A/G
La serie anual uniforme equivalente (A) de un gradiente aritmético G se calcula
multiplicando el valor presente de la ecuación π por la expresión del factor (A/P,i,n)
El equivalente de la cancelación algebraica de P se utiliza para obtener el
factor (A/G,i,n):
A=G(P/G,i,n)(A/P,i,n)=G(A/G,i,n)
La expresión entre corchetes en la ecuación ρ se denomina el factor de gradiente
aritmético de una serie uniforme y se identifica por (A/G,i,n).
Diagrama de conversión de una serie gradiente aritmético a una serie anual uniforme
equivalente:

13. -Cálculos de tasas de interés desconocidas.
La tasa desconocida puede determinarse para por una solución directa de la
ecuación del valor del dinero en el tiempo. Sin embargo, cuando hay pagos no
uniformes o muchos factores, el problema debe resolverse mediante un método de
ensayo y error o numérico. En esta sección se consideran problemas de flujo de
efectivo, serie uniforme, pago único, o la serie gradiente convencional.
Los problemas más complicados de ensayo y error se abordan en el capítulo 7,
que estudia el análisis de tasas de retorno.
Las fórmulas de pago único pueden reordenarse con facilidad y expresarse en
términos de i, pero para las ecuaciones de serie uniforme y de gradientes,
comúnmente es necesario resolver para el valor del factor y determinar la
tasa de interés a partir de las tablas de factores de interés. Ambas situaciones
se ilustran en los ejemplos siguientes.

14. Ejemplo
Si Carol puede hacer una inversión de negocios que requiere un gasto de $3000
ahora con el fin de recibir $5000 dentro de cinco años, ¿cual seria la tasa de
retorno sobre la inversión?
Si Carol puede recibir 7% anual de intereses de un certificado de depósito, ¿cual
inversión debe hacerse?
El diagrama de flujo de efectivo se muestra en la figura 2.19. Dado que hay fórmulas de
pago único involucradas en este problema, la i puede determinarse directamente de la
formula. F=(P/F),i,n) =
3000 = 5000 5
0.600 = 5

15. Conclusión
En resumen por medio del Análisis de valor presente El criterio de
decisión debe incorporar algún índice, medida de equivalencia o base para
su comparación, que resuma las diferencias significativas entre las distintas
propuestas. Las relaciones y ecuaciones desarrolladas en este informe son
los elementos necesarios que permiten realizar las comparaciones entre
dos o más alternativas que tienen igual o diferente vida útil. En ocasiones lo
que se requiere es encontrar el tiempo en el cual se tuvo invertida o fue
hecho un préstamo de una cantidad A de dinero a una determinada tasa de
interés para poder retirar en el futuro o pagar una cantidad B. Para efectos
de no confundir al lector, la cantidad A será el valor presente y la cantidad B
el valor futuro. Para poder encontrar ese tiempo, se toma como punto de
partida la ecuación utilizada para hallar el valor presente y se va
despejando ésta hasta llegar a la fórmula que permite calcular el tiempo a
partir de valor presente.

16. Bibliografía
http://es.scribd.com/doc/52770434/Factores-de-Pago-Unico
http://es.wikipedia.org/wiki/Ingenier%C3%ADa_econ%C3%B3mica
: http://virtual.funlam.edu.co/repositorio/sites/default/files/repositorioa
rchivos/2009/12/ValordelDineroenelTiempo.271.pdf
http://www.slideshare.net/sergio_ayup/unidad-1-6739129
http://www.eco-finanzas.com/diccionario/V/VALOR_PRESENTE_NETO.htm