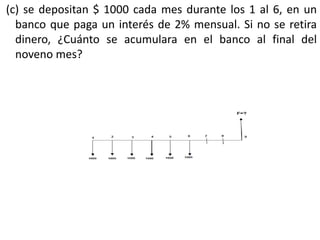
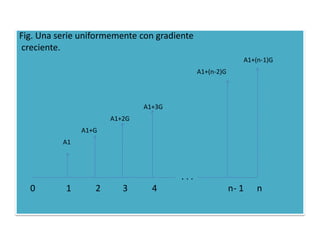
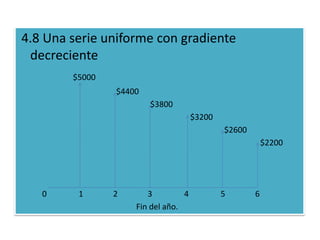
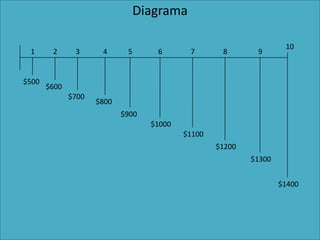
Este documento presenta varias fórmulas matemáticas para calcular valores equivalentes presentes, futuros y anuales en series de pagos uniformes y no uniformes con tasas de interés compuestas de forma continua u anual. Incluye ejemplos numéricos para ilustrar cómo aplicar las fórmulas a diferentes escenarios de flujos de efectivo como ahorros para la jubilación, préstamos y proyectos de inversión entre condados.

1. INSTITUTO TECNOLOGICO SUPERIOR
DE PANUCO
FORMULAS DE INTERES QUE RELACIONAN UNA SERIE
UNIFORME (anualidad) CON SUS VALORES EQUIVALENTES
PRESENTE Y FUTURO

2. La figura 3-6 muestra un diagrama de flujo de efectivo
general que incluye una serie de entradas uniformes
(iguales), cada uno con un montón A, que ocurre al
final de cada unos de los N periodos con un interés
del i%.
Esta serie uniforme suele llamarse anualidad. Observe
que las formulas y tablas que presentaremos se
derivan de modo que A ocurre al final de cada periodo
y de esta forma :

3. 1. P (valor equivalente presente) ocurre un periodo de
interés antes de la primera A (monto uniforme)
2. F (valor equivalente futuro) ocurre al mismo tiempo
que la ultima A, y N periodos después de la P.
3. A (valor equivalente anual) ocurre al final de los
periodos 1 al N, inclusive.
Puede verse la relación temporal para P, A y F en la
figura 3-6.

4. Encuentre F cuando se da A
Si un flujo efectivo de A cantidad de dólares ocurre al
final de cada uno de los N periodos cuya tasa de
interés (utilidad o crecimiento) es del i%, al final del N-
esimo periodo se obtiene el valor equivalente futuro
F, al sumarlos .

5. diagrama de flujo 3.9

6. FORMULA

7. La cantidad de F = A se llama factor del monto compuesto de
la serie uniforme. En la cuarta columna de las tablas del
apéndice C se dan los valores numéricos para este factor
para un amplio rango de valores de i y N. Utilizando el
símbolo funcional ( F/A, i%, N ) para este factor. Por ello la
ecuación anterior se puede expresar así.
F = A( F/A, i%, N )
Mostrándole a continuación unos ejemplos….

8. (a) Suponga que realiza 15 depósitos anuales de $1000 cada
uno en una cuenta bancaria que paga 5% de interés anual.
El primer deposito se hará dentro de un año . ¿Cuánto
dinero puede retirar de esta cuenta bancaria
inmediatamente después del decimoquinto deposito?
F= $1000 (F/A,5%,15)
= $1000(21.5786)
= $21,578.60
El valor de A es de $1000, N es igual a 15 años, e i = 5% por
año. Inmediatamente después del decimoquinto pago, el
monto equivalente futuro es:

9. Determine A cuando se da F
al resolver la ecuación 3-6 y despejar A, entonces que :

10. Por lo tanto la ecuación 3-10 es la relación que permite
encontrar el monto, A de una serie uniforme de flujos de
efectivos al final de N periodos de interés, que equipo
valdría a ( tendría el mismo valor que) su valor equivalente
futuro al final del ultimo periodo .
La cantidad entre corchetes se llama factor del fondo de
amortización. En la sexta columna de las tablas c se
proporcionan valores numéricos para este factor para un
amplio rango de valores de i y N. utilizaremos el símbolo
funcional (A/F, i%, N) para este factor de aquí.
A = F(A/F, i%, N)

11. (b) una estudiante emprendedora planea tener ahorros
personales por un total de $1,000,000. cuando se retire a
los 65 años. Ahora tiene 20 años. Si la tasa de interés anual
de su cuenta de ahorros será del 7%, en promedio, durante
los siguientes 45años ¿Qué cantidad igual debe ahorrar al
final del año para lograr su meta?
A = $1,000,000 (A/F, 7%, 45)
= $1,000,000(0.0035)
= $3,500

12. El monto futuro F, es de $1,000,000. la cantidad anual que
esta estudiante debe colocar en un fondo de amortización
que crezca a $1,000,000 en 45 años al 75 de interés anual
(véase tabla C-10)

13. (c) se depositan $ 1000 cada mes durante los 1 al 6, en un
banco que paga un interés de 2% mensual. Si no se retira
dinero, ¿Cuánto se acumulara en el banco al final del
noveno mes?

14. En el ejemplo la formula va a sumar los seis depósitos de
$1000 a su valor equivalente y los va a depositar al final del
periodo seis, es decir, en el ultimo periodo de la serie de seis
depósitos. Una vez que se ha acumulado cierta cantidad al
final del periodo seis, el dinero se deja depositado tres meses
más, en los cuales ganará 2% de interés mensual.

15. INSTITUTO TECNOLOGICO
SUPERIOR DE PAUNCO.
EQUIPO # 5
“FACTOR DE GRADIENTE”
INTEGRANTES :
Miguel A. Ochoa Contreras
Ubico Cruz Valdez
Javier Navarro Hernández

16. FACTOR PARA UNA SERIE DE PAGOS CON GRADIENTE
UNIFORME.
Los pagos anuales ocurren en muchos casos, de acuerdo
con el patrón propio de una serie de pagos iguales. Por
ejemplo, podría presentarse una serie de pagos que
aumentara uniformemente en la siguiente forma: $100,
$125, $150 y $175y que ocurrieran al final de los años 10.,
20., 30. y 40., respectivamente. De manera similar, podría
presentarse una serie uniformemente decreciente con
valores de $100, $90, $80 y $70 al final de los años 10, 20,
30. y 40., respectivamente. En general, una serie de pagos
que aumenta uniformemente durante n periodos puede
expresarse como A1, A1 + G, A1 + 2G,…A1 + (n − 1)G como
se muestra en la fig. 4.7 en la cual A1 indica el primero de
la serie de pagos al final de cada año y G el cambio anual
en la magnitud de la serie de los pagos.

17. Una manera de evaluar una serie de estas es utilizando
para ello las formulas de interés, que se desarrollaron
previamente, separadamente con cada uno de los pagos
en la serie. Este método conducirá al resultado correcto
pero consumirá una gran cantidad de tiempo. Un
enfoque diferente consiste en reducir la serie de pagos
uniformemente crecientes a una serie equivalente de
pagos iguales de manera que pueda emplearse el factor
de una serie de pagos iguales. Permítase designar
A1= pago al finalizar el primer año;
G= cambio anual o gradiente;
n= el numero de años;
A= el pago anual equivalente igual.

18. Fig. Una serie uniformemente con gradiente
creciente.
A1+(n-1)G
A1+(n-2)G
A1+3G
A1+2G
A1+G
A1
...
0 1 2 3 4 n- 1 n

19. La serie con gradiente puede emplearse también en el
caso de un gradiente uniformemente decreciente.
Supóngase que se desea encontrar la serie de pagos
anuales iguales que es equivalente a la serie con
gradiente decreciente que aparece en la figura 4.8.
visualícese el flujo de caja que aparece en la figura 4.8
como resultado de una sustracción, año por año, de
una serie con gradiente creciente en donde G= $600, a
una serie de pagos anuales de $5000. Al enfocar el
problema en esta forma no es necesario calcular
nuevos factores y la serie de pagos iguales equivalentes
a esta con gradiente decreciente al 9% anual es
A= $5000 - $600(2,2498) =$3650 por año.

20. 4.8 Una serie uniforme con gradiente
decreciente
$5000
$4400
$3800
$3200
$2600
$2200
0 1 2 3 4 5 6
Fin del año.

21. Tres condados adyacentes en florida acordaron
emplear recursos fiscales ya destinados para
remodelar los puentes mantenidos por el condado.
En una junta reciente, los ingenieros de los
condados estimaron que, al final del próximo año, se
depositara un total de $500,000 en una cuenta para la
reparación de los viejos puentes de seguridad dudosa
que se encuentran en los tres condado. Además,
estiman que los depósitos aumentaran en $100,000
por año durante 9 años a partir de ese momento, y
luego cesaran. Determine las cantidades equivalentes
de a) serie anual si los fondos del condado ganaran
intereses a una tasa del 5% anual.

22. Diagrama
10
1 2 3 4 5 6 7 8 9
$500
$600
$700
$800
$900
$1000
$1100
$1200
$1300
$1400

23. Donde:
AT=AA +AG Y AT= AA – AG
Es necesario considerar por separado al gradiente y a
la cantidad base la serie anual total AT.
At= 500+100(A/G,5%,10)=500+100(4.0991)
=$909.91 por año ($909,910)
Y ocurre desde el año 1 hasta el año 10

24. Ejemplo 2:
Una persona piensa abrir una cuenta de ahorros que
paga el 12% anual. Para empezar, esta persona piensa
depositar al final del año $5,000. Sin embargo,
puesto que su salario está creciendo constantemente,
esta persona cree poder incrementar la cantidad a
ahorrar en $1,000 cada año. Si esta misma persona
hiciera depósitos anuales de la misma magnitud, ¿de
que tamaño tendría que ser para que la cantidad
acumulada en 10 años fuera la misma?

25. Datos: Formula:
A1=$5,000
G=$1,000
i=12%
n=10

26. FORMULAS DE INTERES
(COMPOSICION CONTINUA,
PAGOS DISCRETOS)

27. Es la razonable suponer en ciertas evaluaciones
económicas, que la composición continua de
interés representa mas fehacientemente la
situación real que la composición anual. La
suposición de composición continua puede ser
también mas conviene desde un punto de vista
de calculo en el caso de algunas aplicaciones
especificas. En esta sección presenta formulas
que pueden emplearse en aquellos casos en los
cuales parece apropiado hacer pagos anuales
pero compuestos continuamente. Se emplean
los siguientes símbolos:

28. r= La tasa de interés nominal anual.
N=Numero de periodos anuales.
P= Una suma o principal presente.
A=Un pago único, en una serie de n pagos iguales,
hecho al final de cada periodo anual.
F=Una suma futura, n periodos anuales a partir de
hoy, igual a la cantidad compuesta de un
principal presente P, o igual a la suma de los
pagos compuestos A en una serie.
e= Es valor constante y su valor es 2.7182

29.  Composición Discreta
 Composición Continua

30. Ejemplo 1º
Una persona pide prestado una cantidad de $1000
para pagarlo dentro de 5 años a una tasa de interés
del 20% anual. ¿Cuánto pagaría esta persona al
final del quinto año?
DATOS: FORMULA:
r=20%=0.20
n=5 años F=Pern
P=$1000
F=?

31. Sustitucion:
F=Pern
F=1000e(0.2)(5) diagrama de flujo
F=1000e(1) $1000
F=2718.2818
0 1 2 3 4 5
F=?
Esto es, la cantidad a pagar al final del quinto año seria
de $F=2718.28

32. Ejemplo numero 2
 Una persona le pide prestado la cantidad de
$1000 para pagarla dentro de 5 años a un a taza
de interés del 20% anual. Cuanto pagaría esta
persona al final del 5to año?
 Utilizando la ecuación
F=P(1+i)^n
F=10000(1+.2)^5
F=1000(2.4883)=2488.30
Esto es la cantidad a pagar al final del 5to año seria
de $2488.30

33. •Ejemplo 3º
La empresa fabricante de carros Renault firmo un
contrato de $75 millones con ABB de Zúrich, Suiza.
Para automatizar las líneas de montaje de chasis,
los talleres de ensamblado de la carrocería y los
sistemas de control de línea. Si ABB recibirá el
pago dentro de 2 años (cuando los sistemas
queden listos) ¿Cuál es el valor actual del contrato
con un interés del 18% anual?

34. Diagrama de flujo:
F= 75000000
1 2
P=?

35. Formula:

36. Sustitución:
P= $75000000 (0.6976)
P=$ 52326798.3