Este documento presenta los factores de valor presente y futuro para pagos únicos, series uniformes y gradientes aritméticos. Explica cómo calcular cada factor y cómo se pueden usar para evaluar si un proyecto o inversión será rentable considerando el tiempo y la tasa de interés. También cubre cómo calcular tasas de interés desconocidas usando los factores cuando se conocen los montos de dinero invertido y recibido.

1. BACHILLER:
MARIA GODOY
C.I.: 24.492.321
PROFESORA:
ANABEL BENAVIDES

2. INTRODUCCIÓN
En esta presentación se podrán apreciar los diferentes
factores de tiempo y interés (F/P y P/F),( P/A y A/P) y el
(P/G y A/G) sus definiciones, características como se
pueden aplicar y desarrollar sus cálculos los cuales
permiten evaluar si el proyecto o futura inversión será
rentable en un periodo n, esto se puede determinar
rápidamente con la tasa de interés a la cual esté sometida
la inversión y como se encuentra establecidos los
periodos de pago.

3. FACTORES DE PAGO ÚNICO (F/P Y P/F).
Los factores de interés que se desarrollarán, consideran
el tiempo y la tasa de interés. Luego, ellos constituyen el
camino adecuado para la transformación de alternativas
en términos de una base temporal común. Estos factores
son deducidos con base a la generación del interés
compuesto para determinar la cantidad futura o presente
en un momento dado del tiempo. El interés compuesto
se refiere al interés pagado sobre el interés.

4. FACTORES DE PAGO ÚNICO (F/P Y P/F).
 Factor valor Futuro.
F1= P + Pi, deduciendo lo siguiente F1= P(1+i), para el año dos F2=P(1+i) + P(1+i)i,
como el monto del interés y principal se acumula para cada año y se multiplica por
el factor de interés, resultando una potencia para n años. De tal forma que la
fórmula compuesta resulta.
F= P(1+i)ⁿ donde el término entre paréntesis se denomina factor de descuento
 Factor valor Presente.
Este factor es el inverso del factor valor presente en donde la cantidad futura al
enviarla al presente disminuirá su valor debido al factor de descuento.
P= F(1/(1+i)ⁿ) o P= F (1+i)-ⁿ

5. Factor de valor presente de la recuperación
de capital para serie uniforme (P/A y A/P)
El valor presente P de una serie uniforme, puede ser
determinado considerando cada valor de A como un
valor futuro F y utilizando la ecuación con el factor P/F
para luego sumar los valores del valor presente.
 La fórmula general es.
𝑃 = 𝐴 𝑃/𝐴, 𝑖, 𝑛

6. Factor de Valor Presente en una
Serie Uniforme (P/A)
 El valor presente P equivalente de una serie uniforme A
de flujo de efectivo al final del periodo, se determina
considerando cada valor de A como un valor futuro F:
 Los términos entre corchetes representan los factores
(P/F) para los años 1 hasta n, respectivamente. Si se
factoriza A

7. Factor de Valor Presente en una Serie
Uniforme (P/A)
 Para simplificar y obtener el factor P/A, multiplicar esta
ecuación por el factor P/F, es decir 1/(1+i):
 Se resta la ecuación β de la ecuación γ y se simplifica:

8. INTERPOLACIÓN
La interpolación es un proceso matemático para calcular
el valor de una variable dependiente en base a valores
conocidos de las variables dependientes vinculadas,
donde la variable dependiente es una función de una
variable independiente.

9. Factor de Valor Presente en una Serie
Uniforme (P/A)
 Continuando con la Simplificación de la ecuación
anterior:
 Enseguida, en la ecuación anterior se despeja P:

10. Factor de Valor Presente en una
Serie Uniforme (P/A)
 Aparece el factor valor presente serie uniforme
(FVPSU).
 Para todo i ǂ 0

11. Factor Recuperación Capital en Serie
Uniforme (A/P)
 Se conoce el valor presente P y se busca la cantidad
equivalente A de serie uniforme. Entre corchetes
aparece el factor de recuperación de capital (FRC):
 Diagrama de flujo de efectivo.

12. Factor Recuperación Capital en Serie
Uniforme (A/P)
 Factores P/A y A/P
 La función VA también calcula el valor P para una A dada:
=VA(i%,n,A,F)
 De manera similar, el valor A se determina utilizando la función PAGO:
=PAGO(i%,n,P,F)
mj

13. Factores de gradiente aritmética P/G y
A/G.
Un gradiente uniforme es una serie de flujo de efectivo que
aumenta o disminuye en forma uniforme. Es decir, el flujo de
efectivo, bien sea ingreso o desembolso, cambia por la misma
cantidad aritmética cada periodo de interés. La cantidad del
aumento o de la disminución es el gradiente.
 Por ejemplo, si un fabricante de automóviles predice que el
costo de mantener un robot aumentará en $500 anuales
hasta que la máquina haya sido retirada, hay una serie de
gradientes involucrada y la cantidad del gradiente es $500.
En forma similar, si la compañía espera que el ingreso
disminuya en $3000 anualmente durante los próximos 5
años, el ingreso decreciente representa un gradiente
negativo por una suma de $3000 anuales.

14. Factor de Gradiente Aritmético P/G
 En la figura α el valor presente en año 0 sólo del
gradiente es igual a suma de valores presentes de pagos
individuales, donde cada valor se considera como una
unidad futura:
P=G(P/F,i,2)+2G(P/F,1,3)+3G(P/F,i,4)+….+[(n-2)G](P/F,i,n-1)+[(n-1)G](P/F,i,n)
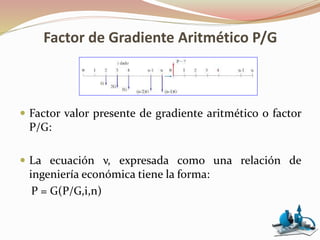
 Factorizando G y aplicando la fórmula P/F:

15. Factor de Gradiente Aritmético P/G
 Al multiplicar ambos lados de θ por (1+i)1 se obtiene:
 Al multiplicar ambos lados de θ por (1+i)1 se obtiene:
 Restar la ecuación θ de la ecuación κ y simplificar:

16. Factor de Gradiente Aritmético P/G
 La expresión entre corchetes (de la izquierda) es igual
a la ecuación β, donde se derivó P/A. Sustituir la forma
cerrada de P/A de la ecuación δ en la ecuación λ y
despejar P:
 La ecuación μ, es la relación general para convertir un
gradiente aritmético G (sin incluir la cantidad base)
para n años en un valor presente en el año 0.
En la figura β se observa cómo se convierte un
gradiente aritmético a un valor presente

17. Factor de Gradiente Aritmético P/G
 Factor valor presente de gradiente aritmético o factor
P/G:
 La ecuación ν, expresada como una relación de
ingeniería económica tiene la forma:
P = G(P/G,i,n)

18. Factor de Gradiente Aritmético A/G.
 La serie anual uniforme equivalente (A) de un
gradiente aritmético G se calcula multiplicando el
valor presente de la ecuación π por la expresión del
factor (A/P,i,n)
El equivalente de la cancelación algebraica de P se utiliza
para obtener el factor (A/G,i,n):
A=G(P/G,i,n)(A/P,i,n)=G(A/G,i,n)

19. Factor de Gradiente Aritmético A/G.
 La expresión entre corchetes en la ecuación ρ se
denomina el factor de gradiente aritmético de una
serie uniforme y se identifica por (A/G,i,n).
Diagrama de conversión de una serie gradiente
aritmético a una serie anual uniforme equivalente.

20. Cálculo de tasas de interés desconocidas.
En algunos casos, se conoce la cantidad de dinero depositado
y la cantidad de dinero recibida luego de un número
especificado de años pero se desconoce la tasa de interés o
tasa de retorno. Cuando hay involucrados un pago único y un
recibo único, una serie uniforme de pagos recibidos, o un
gradiente convencional uniforme de pagos recibido, la tasa
desconocida puede determinarse para “i” por una solución
directa de la ecuación del valor del dinero en el tiempo. Sin
embargo, cuando hay pagos no uniformes, o muchos factores,
el problema debe resolverse mediante un método de ensayo y
error, ó numérico.

21. Cálculo de tasas de interés desconocidas.
 Ejemplo: Si Carolina puede hacer una inversión de
negocios que requiere de un gasto de $3000 ahora con
el fin de recibir $5000 dentro de 5 años, ¿Cuál sería la
tasa de retorno sobre la inversión?
P = F [1/(1+i)n]
3000 = 5000 [1 / (1+i)5]
0.600 = 1 / (1+i)5
i = (1/0.6)0.2-1 = 0.1076 = 10.76%

22. CONCLUSIÓN
Los diferentes factores definidos como el de pago único (F/P y
P/F),( P/A y A/P) y el (P/G y A/G) que consideran el tiempo o
el periodo y la tasa de interés para así construir alternativas
factibles que permitan un mejor flujo de efectivo como se
reflejaron en los procedimientos para calcular cada uno de
los factores desarrollado, como se pudo ver aplicando estos
procedimientos se puede calcular el tiempo y el interés que
tendrá o generara esa inversión para demostrar si el proyecto
planteado y estudiado será rentable. Mientras que el cálculo
de interés desconocido nos permite conocer cómo será
nuestra tasa de interés y así poder calcular cual seria la
mensualidad o anualidad debitada.