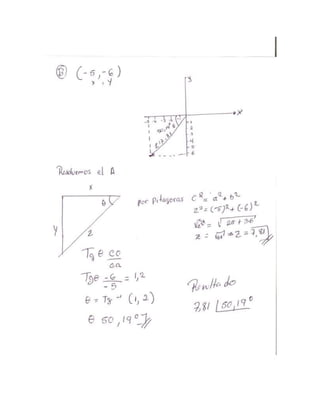
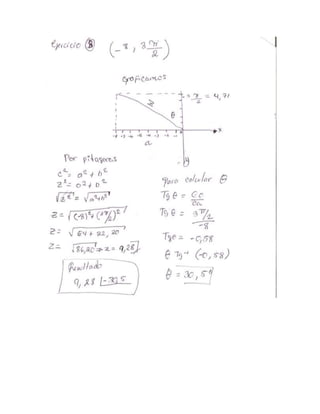
Este documento presenta la resolución de 5 ejercicios de conversión entre coordenadas polares y rectangulares. El primer ejercicio convierte el punto (2,8) a coordenadas polares. El segundo calcula el área dentro de la curva r=1+senθ. El tercero no está resuelto. El cuarto transforma la ecuación r=2cos(3θ) a coordenadas rectangulares. El quinto resulta en una ecuación cúbica.

1. Barquisimeto, 22 de Agosto de 2014
Alumna: Francys Nieto
C.I: 19.726.653
EJERCICIOS
1. Transformar los siguientes puntos de coordenadas rectangulares a coordenadas
polares.
a) (2,8)
X,y
Resolvemos el triangulo por Pitágoras
Aplicamos la tangente para resolver el 휽
푇푔휃 =
퐶푂
퐶푎
푇푔휃 =
8
2
푇푔휃 = 4 휃 = 푇푔−1 4
휃 = 75.96°
RESULTADO:
8,24⁄75,96°
Z = H
8 = Co
2 = Ca
C² = a² + b²
Z²= (2) ² + (8) ²
√푧2 = √(2)2 + (8)²
푍 = √4 + 64 = √68
푍 = 8,24

3. Ejercicio 2): Calcule el área que encierra la curva de la ecuación polar 푟 = 1 + 푠푒푛휃
Es un cardiode
Es simétrica con respecto al eje
휋
2

4. Para formular el área en coordenadas polares se hace lo siguiente
퐴 =
1
2
푎
∫ [(1휃)]2푑휃
푏
휋
2
A=π
휋
2
0
∫ (1 + 푠푒푛휃)2푑휃
Simplificamos y desarrollo productos notables
휋
2
0
A=∫ (1 + 푠푒푛휃 + 푠푒푛2 휃)푑휃
Utilizo la identidad trigonométrica
A=∫ [1 + 2푠푒푛휃 + 1cos2θ
2
휋
2
0
] 푑휃
Por el mínimo común múltiplo
1
2
A=
휋
2
0
∫ (2 + 푠푒푛휃 + 1 − 푐표푠2휃) 푑휃
Sumo términos semejantes
A=
1
2
휋
2
0
∫ (3 + 4푠푒푛휃 − 푐표푠2휃) 푑휃
Resuelvo la integral y evaluó
1
2
A=
= [3휃 − 4푐표푠휃 − 푠푒푛2휃
2
휋
2
0
] ∫
A=
1
2
[3 휋
2
− 4 − (4 cos(표))
A=
1
2
[3 휋
2
− 8]
A= 3π−16
4

5. Ejercicios 3)

8. EJERCICIO (5) Trasformar coordenadas rectangulares a polares
R=2 cos (3휃)
Por la identidad trigonométrica
Cos(3휃)= 4 cos³휃 − 3 푐표푠휃

9. En donde X=r cos휃; 푐표푠 = 푥
푟
푥
푟
Sustituyo r=2 [ 4(
)³ − 3 (푥
푟
) ]
4푥³
푟³
R=2 [
− 3x
r
]
Por factor común
푟 =
2
푟
⌈
4푥 3
푟2 − 3푥⌉
4푥 3
푟2 − 3푥⌉
푟2 = 2 ⌈
Por mínimo común múltiplo
푟
2=2⌈
4푥3 − 3푟2푥
푟2 ⌉
푟4 = 2⌈4푥 3 − 3푟2푥⌉
(푥 2 + 푦2)² = 2⌈4푥 3 − 3(푥 2 + 푦2)푥⌉
(푥 2 + 푦2)² = 8푥 3 − 3푥 3 − 3푥푦2
(푥 2 + 푦2)² = 5푥 3 − 3푥푦3
5푥 3 − 3푥푦2 − (푥 2 + 푦2)² = 0