El documento transforma puntos entre coordenadas rectangulares y polares, calcula áreas de curvas polares, y transforma ecuaciones entre las dos representaciones de coordenadas. Resume los pasos para cada transformación y cálculo de áreas en detalle.

1. 1. Transformar los siguientes puntos de coordenadas rectangulares a coordenadas polares: (1 pt.
c/u)
a. (2,8) b. (−5, −6) c. (√2,
1
5
)
-5
B - 6
x
Y
2
8
A
a) El punto A está en el primer cuadrante:
Y
√2
1/5
C
x
Y
푟 = √22 + 82 = √4 + 64 = √68 = √4 ∙ 17 = 2√17
푡푎푛휃 =
8
2
⇒ 휃 = tan−1(4) = 75,96°
Luego el punto A, es:
퐴(2√17; 75,96°)
b) El punto B está en el tercer cuadrante:
푟 = √(−5)2 + (−6)2 = √25 + 36 = √71
푡푎푛휃 =
−6
−5
⇒ 휃 = tan−1(1,2) = 230,19°
Luego el punto B, es:
퐵(√71; 230,19°)
c) El punto C está en el primer cuadrante:
푟 = √(√2)
2
+ (1/5)2 = √2 + 1/25 = √21/25 =
x
√21
5
푡푎푛휃 =
1/5
√2
1
5√2
⇒ 휃 = tan−1 (
) = 8,05°
Luego el punto C, es:
√21
5
퐶 (
; 8,05°)
2. Calcula el área que encierra la curva de ecuación polar 퐫 =ퟏ +퐬퐞퐧 훉. (2 pts.)
Solución:

2. 퐴 = 2 [
1
2
휋
2
∫ 푟2푑푟
−
휋
2
]
휋
2
퐴 = ∫ (1 + 푠푒푛휃)2푑푟
−
휋
2
퐴 =
1
2
휋
2
∫ (1 + 2푠푒푛휃 + 푠푒푛2휃)푑푟
−
휋
2
퐴 =
1
2
∫ (1 + 2푠푒푛휃 +
1 + 푐표푠2휃
2
) 푑푟
휋
2
−
휋
2
퐴 =
1
2
∫ (1 + 2푠푒푛휃 +
1
2
+
1
2
푐표푠2휃) 푑푟
휋
2
−
휋
2
퐴 =
1
2
∫ (2푠푒푛휃 +
3
2
+
1
2
푐표푠2휃) 푑푟
휋
2
−
휋
2
퐴 =
1
2
(−2푐표푠휃 +
3휃
2
+
1
4
푠푒푛2휃)|
−
휋
2
휋
2
퐴 =
1
2
휋
2
[(−2푐표푠 (
) +
3
2
∙
휋
2
+
1
4
푠푒푛휋) − (−2푐표푠 (−
휋
2
) +
3
2
∙ (−
휋
2
) +
1
4
푠푒푛(−휋))]
퐴 =
1
2
[(−2 ∙ 0 +
3
2
∙
휋
2
+
1
4
∙ 0) − (−2 ∙ 0 −
3휋
4
+
1
4
∙ 0)]
퐴 =
1
2
(
3휋
4
+
3휋
4
)
퐴 =
3휋
4
푢푙2
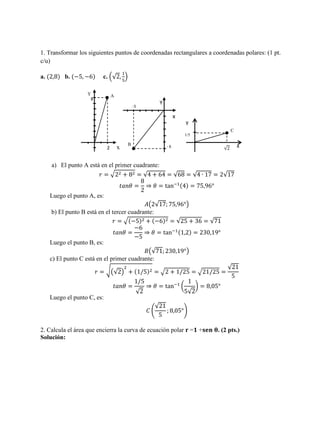
3. Transformar los siguientes puntos de coordenadas rectangulares a coordenadas polares: (1 pt.
c/u)
a. (2,
휋
4
)
푥 = 푟 ∙ 푐표푠휃 푦 푦 = 푟 ∙ 푠푒푛휃
휋
4
푥 = 2 ∙ 푐표푠 (
휋
4
) 푦 푦 = 2 ∙ 푠푒푛 (
)

3. 푥 = 2 ∙
√2
2
푦 푦 = 2 ∙
√2
2
푥 = √2 푦 푦 = √2
(√2, √2)
b. (−8,
3휋
2
)
푥 = 푟 ∙ 푐표푠휃 푦 푦 = 푟 ∙ 푠푒푛휃
3휋
2
푥 = −8 ∙ 푐표푠 (
) 푦 푦 = −8 ∙ 푠푒푛 (
3휋
2
)
푥 = −8 ∙ 0 푦 푦 = −8 ∙ (−1)
푥 = 0 푦 푦 = 8
(0, 8)
c. (−
1
2
,
5휋
4
)
푥 = 푟 ∙ 푐표푠휃 푦 푦 = 푟 ∙ 푠푒푛휃
푥 = −
1
2
5휋
4
∙ 푐표푠 (
) 푦 푦 = −
1
2
∙ 푠푒푛 (
5휋
4
)
푥 = −
1
2
∙ (−
√2
2
) 푦 푦 = −
1
2
∙ (−
√2
2
)
푥 =
√2
4
푦 푦 =
√2
4
√2
4
(
,
√2
4
)
4. Calcula el área que encierra la curva de ecuación polar 퐫 = ퟒ(ퟐ훉) (2 pts.)
Solución:
Esta rosa posee los tres tipos de simetría por lo que:
퐴 = 8 [
1
2
휋/4
∫ 푟2
0
휋/4
푑휃] = 4 ∫ (4 ∙ cos(2휃))2
0
푑휃
휋/4
퐴 = 4 ∫ 16 ∙ 푐표푠2 (2휃)
0
푑휃 = 64 ∫
1 + 푐표푠4휃
2
휋/4
0
푑휃

4. 퐴 = 64 ∫
1 + 푐표푠4휃
2
휋/4
0
휋/4
푑휃 = 32 ∫ (1 + 푐표푠4휃)
0
푑휃
퐴 = 32 (휃 +
1
4
휋/4
푠푒푛4휃)|
0
= 32 [(
휋
4
+
1
4
푠푒푛(휋)) − (0 +
1
4
푠푒푛(0))]
휋
4
퐴 = 32 [(
+ 0) − (0 + 0)]
퐴 = 8휋푢푙2
5. Transformar la siguiente ecuación de variables polares a rectangulares:(1,5 pts.) 퐫=ퟐ퐜퐨퐬 (ퟑ훉)
Solución:
r = 2cos (3θ) = 2 ∙ cos (2θ + θ)
r = 2 ∙ [cos (2θ) ∙ 푐표푠θ − senθ ∙ 푠푒푛(2θ)]
r = 2 ∙ [(cos2 θ − sen2θ)푐표푠θ − senθ ∙ 2푠푒푛θ ∙ cosθ]
r = 2 ∙ (cos3 θ − 푐표푠θ ∙ sen2θ − 2sen2θ ∙ cosθ)
r = 2 ∙ (cos3 θ − 3sen2θ ∙ cosθ)
r = 2 cos3 θ − 6sen2θ ∙ cosθ
Multiplicando por r3 cada término de la ecuación:
r4 = 2r3 cos3 θ − 6r3sen2θ ∙ cosθ
Descomponiendo y asociando:
r4 = 2r3 cos3 θ − 6r2sen2θ ∙ rcosθ
Propiedad de la potenciación:
(r2)2 = 2(r ∙ cos θ)3 − 6(r ∙ senθ)2 ∙ (rcosθ)
(x2 + y2)2 = 2x3 − 6y2 ∙ x
Factor común:
(x2 + y2)2 = 2푥(x2 − 3y2)
6. Transformar la siguiente ecuación de variables rectangulares a variables polares: (1,5 pts.)
퐱ퟐ−ퟐ퐲ퟐ=ퟒ(퐱+퐲)ퟐ
Solución:
Puesto que:
푥 = 푟 ∙ 푐표푠휃 ∧ 푦 = 푟 ∙ 푠푒푛휃
Sustituimos en la ecuación dada:
(푟 ∙ 푐표푠휃)2 − 2(푟 ∙ 푠푒푛휃)2 = 4(푟 ∙ 푐표푠휃 + 푟 ∙ 푠푒푛휃)2
푟2 ∙ cos2 휃 − 2푟2 ∙ 푠푒푛2휃 − 4[푟(푐표푠휃 + 푠푒푛휃)]2 = 0
푟2 ∙ [(cos2 휃 − 2푠푒푛2휃) − 4(cos2 휃 + 2푠푒푛휃 ∙ 푐표푠휃 + 푠푒푛2휃)] = 0
푟2 = 0 ∨ 푐표푠2 휃 − 2푠푒푛2휃 − 4 푐표푠2 휃 − 8푠푒푛휃 ∙ 푐표푠휃 − 4푠푒푛2휃 = 0
푟 = 0 ∨ −3 푐표푠2 휃 − 8푠푒푛휃 ∙ 푐표푠휃 − 6푠푒푛2휃 = 0