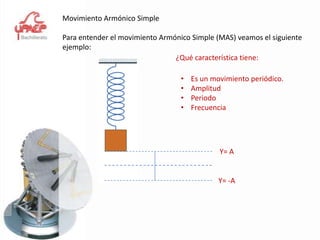
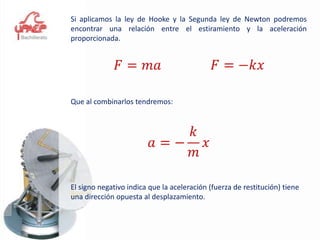
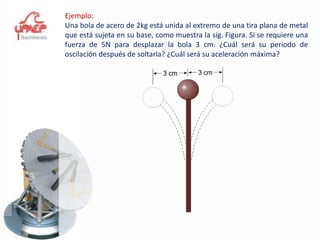
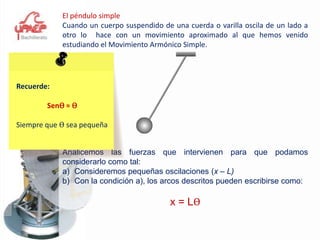
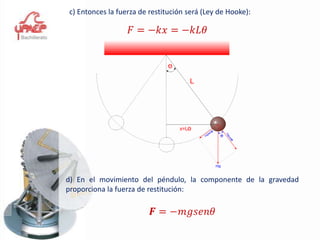
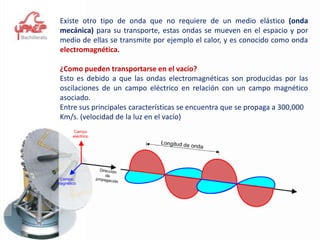
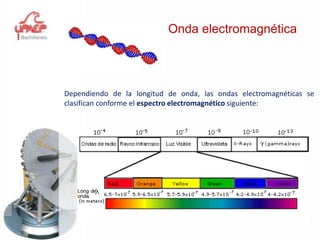
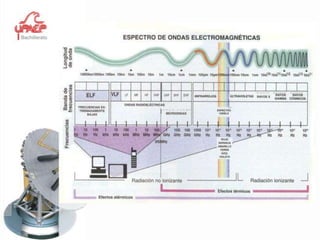
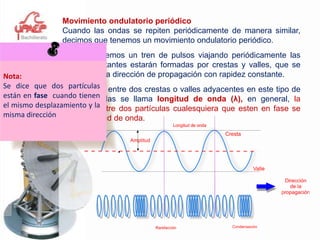
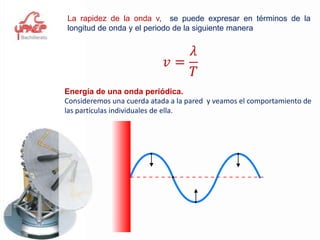
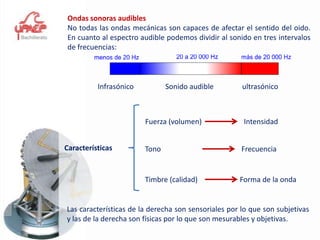
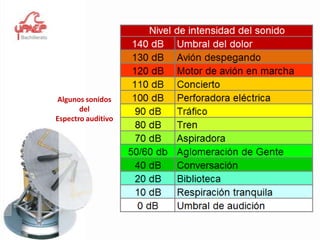
Este documento presenta información sobre el tema de física "Movimiento Armónico Simple". Explica conceptos clave como amplitud, período, frecuencia y las expresiones matemáticas que describen el desplazamiento, velocidad y aceleración de un oscilador armónico. También cubre temas como el péndulo simple y la ley de Hooke, y proporciona ejemplos y problemas para que los estudiantes practiquen.

1. Temas selectos de física IÁrea propedéutica: Tecnológicas e IngenieríasTemas selectos de física IÁrea propedéutica: Tecnológicas e Ingenierías

2. del perfil del estudianteSustenta una postura personal sobre temas de interés y relevancia general, considerando otros puntos de vista de manera crítica y reflexiva.

3. Participa y colabora de manera efectiva en equipos diversos.Competencias disciplinares6.-valora las preconcepciones personales o comunes sobre diversos fenómenos naturales a partir de evidencias científicas.7.-Explicita las nociones científicas que sustentan los procesos para la solución de problemas cotidianos. 8.- Obtiene, registra y sistematiza la información para responder a preguntas de carácter científico, consultando fuentes relevantes y realizando experimentos pertinentes.

4. Iconografía

5. Mecánica ondulatoriaMovimiento armónico simple (MAS)Conceptos fundamentalesAmplitudFaseFrecuenciaPeriodo Tipos de pénduloSimple CompuestoLey de Hooke Movimiento ondulatorioCaracterísticas de una ondaTipos de ondasMecánicasElectromagnéticas Velocidad de una ondaEnergía de una onda periódica.Principio de superposiciónOndas estacionarias SonidoProducción de una onda sonoraRapidez del sonidoOndas sonoras audiblesTono y timbreInterferenciaEfecto DopplerUnidad I

6. Evaluación:Formativa 50%

7. Participación 15%

8. Actividades 35%

9. Sumativa 45%

10. Examen 40%

11. Portafolio de evidencias 5%

12. Autoevaluación y Coevaluación5%

13. Actividad 1 (35 min)Cuéntame de tiCada uno de los miembro de la pareja, preguntaran al otro de su aficiones, intereses, el porque de la elección de el área (tecnológicas), etc. (10 min.)Cada uno integrará la información recabada en una cuartilla. (10 min)Tomando como base la cuartilla elaborada, cada integrante presentara al grupo a su compañero. (15 min)Entregar actividad para calificación e integrar a portafolio de evidencias.

14. Revisa el siguiente video http://www.youtube.com/watch?v=Cw9eFeVY74IInvestiga que es el Movimiento Armónico simple, identificando sus principales elementos, para ello utiliza el video, libros o revistas especializadas y realiza un documento con los resultados de la investigación.Fecha de entrega 17 de agosto de 2011.

15. Movimiento Armónico SimplePara entender el movimiento Armónico Simple (MAS) veamos el siguiente ejemplo:¿Qué característica tiene:Es un movimiento periódico.

16. Amplitud

17. Periodo

18. FrecuenciaY= AY= -A

19. Lo anterior nos lleva primero a definir que es un movimiento periódico:Es aquel en el que un cuerpo se mueve de un lado a otro, sobre una trayectoria fija y regresa a su posición y velocidad después de un intervalo de tiempo definido .Por lo que podemos decir que el MAS es un movimiento periódico que ocurre en ausencia de fricción y es producido por una fuerza de restitución directamente proporcional al desplazamiento y tiene una dirección opuesta a éste.Periodo (T): Tiempo en que el cuerpo regresa al punto de partida (realiza una oscilación completa), esto es, para el caso del ejemplo cuando el cuerpo va de +A a –A y regresa a +A.Frecuencia (f): es el número de oscilaciones por unidad de tiempo, que se relaciona con el período por medio de la siguiente relación:𝑓=1𝑇

20. La frecuencia en el Sistema Internacional se mide en oscilaciones/segundo que es conocido como Hertz (Hz).Nuevamente observemos el comportamiento del MAS:Qué podemos decir del movimiento de la partícula:Desplazamiento𝑥=𝐴𝑐𝑜𝑠2𝜋𝑓

21. Considerando que la el cuerpo se mueve entre los puntos –A y A , bajo la influencia de una fuerza de restitución; en dichos puntos la velocidad debe ser cero y el desplazamiento es máximo; de igual manera, si el desplazamiento es cero la velocidad es máxima (centro).Velocidad𝑣=−2𝜋𝑓𝐴𝑠𝑒𝑛(2𝜋𝑓𝑡) Es importante notar que la expresión anterior será mayor cuando (considere los valores de la función seno)𝑠𝑒𝑛2𝜋𝑓𝑡=1 Por lo tanto tendremos:𝑣𝑚𝑎𝑥=−2𝜋𝑓𝐴

22. AceleraciónComo el MAS esta sometido a una fuerza de restitución, cuando nos encontremos en el punto –A o el punto A, la velocidad es cero y la fuerza de restitución será máxima y entonces la aceleración también será máxima. Cuando la masa se aproxime a su punto de equilibrio la fuerza de restitución y por consiguiente la aceleración son cero y como lo mencionamos antes la velocidad será máxima.𝑎=−4𝜋2𝑓2𝑥 FrecuenciaCon la información que se tiene para x, v y a, podemos deducir la siguiente expresión para la frecuencia:𝑓=12𝜋−𝑎𝑥

23. Luego entonces:Periodo𝑇=2𝜋−𝑥𝑎 Una herramienta útil para el estudio del MAS es la ley de Hooke (Robert Hooke) que se utiliza para los resortes y que relaciona el estiramiento del resorte del resorte con la fuerza aplicada. Hooke descubre que cuando una fuerza (F) actúa sobre un resorte produce un alargamiento (x) que matemáticamente se expresa como:𝐹=−𝑘𝑥 Esta ley se aplica no solo para el caso de los resortes, sino aplica a deformaciones de cuerpos elásticos.

24. Si aplicamos la ley de Hooke y la Segunda ley de Newton podremos encontrar una relación entre el estiramiento y la aceleración proporcionada.𝐹=𝑚𝑎 𝐹=−𝑘𝑥 Que al combinarlos tendremos: 𝑎=−𝑘𝑚𝑥 El signo negativo indica que la aceleración (fuerza de restitución) tiene una dirección opuesta al desplazamiento.

25. Ejemplo:Una bola de acero de 2kg está unida al extremo de una tira plana de metal que está sujeta en su base, como muestra la sig. Figura. Si se requiere una fuerza de 5N para desplazar la bola 3 cm. ¿Cuál será su periodo de oscilación después de soltarla? ¿Cuál será su aceleración máxima?

26. En resumen:𝑥=𝐴𝑐𝑜𝑠2𝜋𝑓𝑡 𝑣=−2𝜋𝑓𝐴𝑠𝑒𝑛2𝜋𝑓𝑡 𝑎=−4𝜋2𝑓2𝑥 𝑎=−𝑘𝑚𝑥 𝐹=−𝑘𝑥 𝑓=12𝜋−𝑎𝑥 𝑇=2𝜋−𝑥𝑎 𝑓=12𝜋𝑘𝑚 𝑇=2𝜋𝑚𝑘

27. Vea el siguiente video y elabore un trabajo (Mínimo 4 cuartillas) en donde explique el movimiento armónico simple, incluya las expresiones matemáticas necesarias, además, considere aquellas no vistas en clase, incluya conclusiones personales en donde describa lo aprendido además de sus reflexiones sobre el tema.Fecha de entrega (jueves 25)

28. Preguntas:Exponga varios ejemplos de movimiento que se correspondan al MASSi se duplica la amplitud A de un cuerpo que se mueve con MAS ¿Qué efecto tendrá en (a) el periodo, (b) la velocidad máxima y (c) la aceleración máxima.Una masa m1de 2kg se mueve en MAS con una frecuencia f1, ¿Qué masa m2 hará que el sistema oscile al doble de esa frecuencia?Tarea (personal):Resolver los problemas 14.1, 14.3, 14.5, 14.15, 14.17, 14.19, 14.25, 14.27.Tippens E. Paul, “Física Conceptos y aplicaciones”, séptima edición, Mc Graw Hill, pags. 297-300,Fecha de entrega lunes 30 de agosto Examen Tema Lunes 30 de agosto.

29. Trabajo y energía en el movimiento Armónico SimplePara el caso del oscilador armónico simple tenemos que la energía potencial (Posición) se puede expresar como:𝑈=12𝑘𝑥2 Y la energía cinética (Movimiento) se expresa 𝐾=12𝑚𝑣2 Y la energía total será𝐸=12𝑘𝑥2+12𝑚𝑣2

30. El oscilador armónico por su propia característica es un sistema conservativo, lo que nos indica que se cumple la ley de la conservación de la energía que podemos expresar de la siguiente manera:Energía Inicial (Eo) = Energía Final (Ef) 𝑈0+𝐾0=𝑈𝑓+𝐾𝑓 Y sustituyendo las expresiones tenemos:12𝑘𝑥02+12𝑚𝑣02=12𝑘𝑥𝑓2+12𝑚𝑣𝑓2 Si lo que se desea es calcular la velocidad v de una masa que se mueve con MAS y sin fricción, consideremos un punto cualquiera (x) y un punto en un extremo (A), la masa se moverá del punto A al punto x seleccionado.

31. 12𝑘𝑥2+12𝑚𝑣2=12𝑘𝐴2 Despejando la velocidad tendremos:𝑣=𝑘𝑚𝐴2−𝑥2 Para el caso de la velocidad máxima (x=0)𝑣=𝑘𝑚A

32. El péndulo simpleCuando un cuerpo suspendido de una cuerda o varilla oscila de un lado a otro lo hace con un movimiento aproximado al que hemos venido estudiando el Movimiento Armónico Simple.Recuerde:Senϴ ≈ ϴSiempre que ϴ sea pequeñaAnalicemos las fuerzas que intervienen para que podamos considerarlo como tal:Consideremos pequeñas oscilaciones (x – L)Con la condición a), los arcos descritos pueden escribirse como:x = Lϴ

33. c) Entonces la fuerza de restitución será (Ley de Hooke):𝐹=−𝑘𝑥=−𝑘𝐿𝜃 d) En el movimiento del péndulo, la componente de la gravedad proporciona la fuerza de restitución:𝑭=−𝑚𝑔𝑠𝑒𝑛𝜃

34. Igualando c) y d), considerando a) tenemos: 𝑓=−𝑘𝐿𝜃=−𝑚𝑔𝜃 Despejando𝐿𝑔=𝑚𝑘 Y sustituyendo en las ecuaciones que tenemos para el período obtenemos una ecuación para el período del péndulo simple 𝑇=2𝜋𝐿𝑔 Observe que el período de oscilación no depende de la masa del objeto ni de la Amplitud de la oscilación, depende únicamente de la longitud (L) de la cuerda o varilla

35. Tarea :Resolver los problemas 14.36, 14.37, 14.38, 14.39.TippensE. Paul, “Física Conceptos y aplicaciones”, séptima edición, Mc Graw Hill, pags. 297-300,Fecha de entrega miércoles 7 de septiembre

36. Movimiento OndulatorioActividadDescribe con tus palabras que se entiende por una onda mecánica.

37. Presenta algunos ejemplos de ellas.

38. Como podemos utilizar éstas en beneficio del hombre.El movimiento ondulatorio, es provocado por una perturbación en un medio, de manera tal que una cantidad de energía se transmite por él (medio) mediante la agitación de las partículas del medio en donde se propaga.Definiciones:A la propagación de la energía pro medio de una perturbación en un medio, y no por el movimiento del medio mismo, se le llama movimiento ondulatorio.

39. Una onda mecánica es una perturbación física en un medio elástico.

40. TransversalesTipos de ondas (Por el tipo de movimiento que generan en una parte determinada del medio)LongitudinalesOnda transversalEn una onda transversal, la vibración de las partículas individuales del medio es perpendicular a la dirección de propagación de la onda.

41. Onda longitudinalEn una onda longitudinal, la vibración de las partículas individuales es paralela a la dirección de la propagación de la onda

42. Existe otro tipo de onda que no requiere de un medio elástico (onda mecánica) para su transporte, estas ondas se mueven en el espacio y por medio de ellas se transmite por ejemplo el calor, y es conocido como onda electromagnética.¿Como pueden transportarse en el vacío?Esto es debido a que las ondas electromagnéticas son producidas por las oscilaciones de un campo eléctrico en relación con un campo magnético asociado.Entre sus principales características se encuentra que se propaga a 300,000 Km/s. (velocidad de la luz en el vacío)

43. Onda electromagnéticaDependiendo de la longitud de onda, las ondas electromagnéticas se clasifican conforme el espectro electromagnético siguiente:

45. Movimiento ondulatorio periódicoCuando las ondas se repiten periódicamente de manera similar, decimos que tenemos un movimiento ondulatorio periódico.Cuando tenemos un tren de pulsos viajando periódicamente las ondas resultantes estarán formadas por crestas y valles, que se mueven en la dirección de propagación con rapidez constante.La distancia entre dos crestas o valles adyacentes en este tipo de tren de ondas se llama longitud de onda (λ), en general, la distancia entre dos partículas cualesquiera que esten en fase se llama longitud de onda.Nota:Se dice que dos partículas están en fase cuando tienen el mismo desplazamiento y la misma dirección

46. La rapidez de la onda v, se puede expresar en términos de la longitud de onda y el periodo de la siguiente manera𝑣=𝜆𝑇 Energía de una onda periódica.Consideremos una cuerda atada a la pared y veamos el comportamiento de las partículas individuales de ella.

47. Si nos fijamos en una sola de las partículas del medio, podemos observar que cada una de ellas se mueve con un movimiento armónico simple. El contenido de energía de una onda puede analizarse considerando el movimiento de armónico de las partículas en forma individual.La energía total de una partícula es:𝐸=𝑈+𝐾=𝐾𝑚𝑎𝑥 =12𝑚𝑣𝑚𝑎𝑥2=12𝑚2𝜋𝑓𝐴2 𝐸=2𝜋2𝑓2𝐴2𝑚