Vibraciones y Ondas

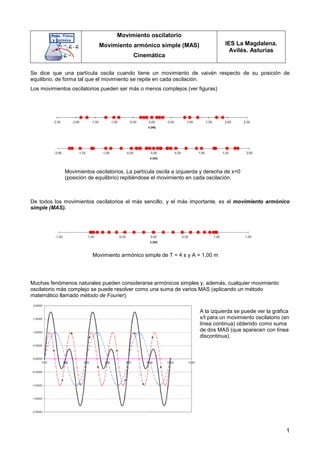
1
Movimiento oscilatorio
Movimiento armónico simple (MAS)
Cinemática
IES La Magdalena.
Avilés. Asturias
Se dice que una partícula oscila cuando tiene un movimiento de vaivén respecto de su posición de
equilibrio, de forma tal que el movimiento se repite en cada oscilación.
Los movimientos oscilatorios pueden ser más o menos complejos (ver figuras)
De todos los movimientos oscilatorios el más sencillo, y el más importante, es el movimiento armónico
simple (MAS).
Muchas fenómenos naturales pueden considerarse armónicos simples y, además, cualquier movimiento
oscilatorio más complejo se puede resolver como una suma de varios MAS (aplicando un método
matemático llamado método de Fourier).
A la izquierda se puede ver la gráfica
x/t para un movimiento oscilatorio (en
línea continua) obtenido como suma
de dos MAS (que aparecen con línea
discontinua).
Movimientos oscilatorios. La partícula oscila a izquierda y derecha de x=0
(posición de equilibrio) repitiéndose el movimiento en cada oscilación.
Movimiento armónico simple de T = 4 s y A = 1,00 m

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Movimiento armónico simple (MAS)
2
ω
sen ( ) cos ( )
cos( ) sen ( )
α + α =
α = − α
2 2
2
1
1
v A cos t A sen ( t) A A sen ( t)
A x A x
v A x
= ω ω = ω − ω = ω − ω ω =
= ω − ω = ω −
= ω −
2 2 2 2 2 2
2 2 2 2 2 2
2 2
1
Un ejemplo de MAS es el de la proyección sobre el diámetro de la circunferencia de la posición de un punto
que gira con velocidad angular constante:
La posición del punto sobre el diámetro queda
determinada por la ecuación:
Donde: x = posición (elongación)
A= Amplitud (elongación máxima)
= Velocidad angular de giro (en rad/s)
= Fase
Esta ecuación puede servir también para definir el
MAS: un cuerpo se mueve con MAS cuando su
posición responde a la ecuación anterior.
Podemos obtener la expresión que nos da la velocidad derivando la expresión anterior respecto del tiempo:
Podemos expresar la velocidad en función de la posición (x) del punto teniendo en cuenta que:
Por tanto:
La velocidad, como se ve, no es constante, es una función cosenoidal del tiempo. Con el fin de conocer la
rapidez con la que varía calculamos la aceleración derivando, una vez más, la velocidad respecto del
tiempo:
La aceleración también podemos expresarla en función de la posición, x:
x A sen( t)= ω
dx
v A cos( t)
dt
= = ω ω
d x dv
a A sen( t)
dt dt
= = = − ω ω
2
2
2
a A sen( t) x
a x
= − ω ω = − ω
= − ω
2 2
2
Movimiento armónico simple. MAS
Observar que el movimiento no es uniformemente
acelerado ya que la aceleración varía (es función
del tiempo).
( t)ω

3
f
T T
π
ω = = π = π
2 1
2 2
( )
( ) ( )
( ) ( )
x A sen t A sen f t
T
v A cos t A f cos f t
T T
v A sen t A f sen f t
T T
π 
= = π 
 
π π   
= = π π   
   
π π   
= − = − π π   
   
2
2
2
2
2 2
2 2
2 2
2 2
Las expresiones anteriores pueden escribirse en función del periodo del movimiento,T (tiempo que tarda en
dar una oscilación completa) o de la frecuencia f (número de oscilaciones por segundo) recordando que:
O sea:
Aunque estemos trabajando solo con la parte escalar de las magnitudes no conviene olvidar que la posición
queda fijada por un vector de posición ( ), y que tanto la velocidad como la aceleración son vectores, cuya
dirección y sentido quedan fijados por la del vector unitario
NOTA: Observar que para un x dada (supongamos que está situada a la derecha del origen) la
velocidad tiene dos valores posibles (ver expresión que da v en función de x), correspondientes al
valor de la raíz cuadrada con signo positivo o negativo, lo que indica que en una determinada
posición el punto puede moverse hacia la derecha (movimiento de ida) o hacia la izquierda
(movimiento de vuelta).
Siempre que el punto se sitúe a la derecha (x positiva), la aceleración apunta hacia la izquierda y
cuando está a la izquierda (x negativa), hacia la derecha.
Recordemos que cuando un punto se mueve con MAS oscila a izquierda y derecha de su posición de
equilibrio. La trayectoria del punto (que se repite en cada oscilación) puede observarse en las gráficas
siguientes, donde las posiciones se han fijado a intervalos regulares de 0,1 s:
r
→
v v i
→ →
=
i
→
r x i
→ →
=
a ( x) i
→ →
= − ω2
i
→
Representaciones gráficas x/t. Valores extremos de v y a

4
Podemos hacer ahora una representación gráfica de
valores de x (posición del punto) respecto del tiempo para
hacernos una idea de cómo varía x en función de t (ver
gráfica a la izquierda)
La gráfica se corresponde con la de un MAS de A = 1,00 m
y T = 2,00 s. Observar que el movimiento se repite a
intervalos de 2 s.
En la gráfica v/t se observa que la velocidad adquiere su
valor máximo positivo en el origen (movimiento hacia la
derecha), decrece luego hasta hacerse nula para t =0,5 s
(x= A) y a partir de ahí adquiere valores crecientes, pero
negativos (movimiento hacia la izquierda), alcanza su
máximo valor negativo para t=1,0 s (paso por el origen
hacia la izda), comienza a decrecer (signo negativo,
movimiento hacia la izda), se anula para t=1,5 s (x =- A) y
a continuación toma valores positivos crecientes
(movimiento hacia la dcha).
Estudiando la gráfica a/t vemos que la aceleración tiene
un valor nulo en el origen, adquiere valores crecientes y
negativos (apunta hacia la izda) hasta su valor máximo
negativo para t=0,5 s (x=A) y a partir de ahí comienza a
disminuir manteniendo el signo negativo, se anula para t=
1,0 s (paso por el origen hacia la izda) y comienza a
crecer apuntando hacia la dcha. (signo positivo). Adquiere
su valor máximo positivo para t =1,5 s (x = - A) y,
finalmente, decrece hasta anularse cuando vuelve a pasar
por el origen.
También podemos estudiar los valores extremos de v y a partiendo de las fórmulas que las relacionan con
la elongación, x:
Comentario Comentario
x= 0
(Mov. hacia la dcha)
Origen. Valor máx.
Mov. hacia la dcha.
a = 0
Origen. Movimiento
hacia la dcha.
x = A v = 0
Máx. alejamiento a
la dcha.
Valor máx. Aceleración
hacia la izda.
x= 0
(Mov. hacia la izda)
Origen. Valor máx.
Mov. hacia la izda.
a = 0
Origen. Movimiento
hacia la izda.
x= - A v = 0
Máx. alejamiento a
la izda.
Valor máx. Aceleración
hacia la dcha.
v A x= ± ω −2 2 a x= − ω2
v A= ω
a A= − ω2
v A= − ω
a A= ω2
Valores v y a
Valores x
x =Ax = - A
a= 0 v max
v max a= 0
a max v= 0a maxv= 0 va
v a
va
v a

5
Ejemplo 1
Un punto oscila con MAS de periodo 4,00 s y amplitud 2,00 m.
a) Escribir la ecuación del movimiento.
b) Determinar el valor de la elongación, velocidad y aceleración para t = 0,75 s y 2,34 s
Solución:
a)
b)
Ejemplo 2
Un punto oscila con MAS de ecuación .
a) Determinar su amplitud, periodo y frecuencia.
b) Determinar los valores extremos de x, v y a y realizar un esquema.
Solución:
a) Comparando la ecuación general del MAS con la dada en el enunciado:
x A sen ( t) A sen t sen t sen t
T
x sen t
π π π     
= ω = = =     
     
π 
=  
 
2 2
2 2
4 2
2
2
(t , )
(t , )
x sen t sen , , m (situado a la derecha del origen)
x sen t sen , , m (situado a la izquierda del origen)
=
=
π π   
= = =   
   
π π   
= = = −   
   
0 75
2 34
2 2 0 75 1 84
2 2
2 2 2 34 1 02
2 2
v A cos ( t) A cos t cos t cos t
T T
v cos t
π π π π π     
= ω ω = = = π     
     
π 
= π  
 
2 2 2 2
2
4 4 2
2
(t , )
(t , )
v cos t cos , , m / s (moviéndose hacia la derecha)
v cos t cos , , m / s (moviéndose hacia la izquierda)
=
=
π π   
= π = π =   
   
π π   
= π = π = −   
   
0 75
2 34
0 75 1 20
2 2
2 34 2 70
2 2
a A sen ( t) A sen t sen t sen t
T T
a sen t
π π π π π π       
= − ω ω = − = − = −       
       
π π 
= −  
 
2 2 2
2
2
2 2 4 2
2
16 4 2 2
2 2
(t , )
(t , )
a sen t sen , , m / s (apunta hacia la izquierda)
a sen t sen , , m / s (apunta hacia la derecha)
=
=
π π π π   
= − = − = −   
   
π π π π   
= − = − =   
   
2 2
2
0 75
2 2
2
2 34
0 75 4 55
2 2 2 2
2 34 2 51
2 2 2 2
x , sen( t)= π0 5
x A sen( t)
T
π
=
2
x , sen( t)= π0 5
Se deduce que A = 0,5 m; T = 2,00 s y f = 1/T= 1/2 s
-1
= 0,5 s
-1

6
b) La elongación varía entre los valores x = 0, x = A (valor máx. a la derecha) y x = - A (valor máx. a
la izda).
Podemos calcular los valores de v en esos puntos utilizando la ecuación :
Para calcular los valores extremos de a usamos la ecuación:
Ejemplo 3
Determinar la ecuación de un punto que oscila con MAS si cuando se encuentra en x= 0,50 m tiene
una velocidad de 1,30 m/s y una aceleración de - 2 m/s
2
Solución:
La ecuación será por tanto:
v A x= ω −2 2
máx
Para x v A A A
T
π
= ⇒ = ω − = ±ω = ± = ±2 2 2
0 0
π
2
máx
, m , m / s
s
v , m / s (Valor máx. Signo hacia la dcha, negativo hacia la izda)
Para x A v A A ; x
= ± π
= ± π +
= ⇒ = ω − = =2 2
0 5 0 5
0 5
0 0
a x= − ω2
máx
máx
máx
máx
Para x a
m
Para x A a A A , m ,
T s s
m
a , (Valor máximo. El signo indica que apunta hacia la izda)
s
m
Para x A a A A ( , m) ,
T s s
m
a , (V
s
= ⇒ =
 π π 
= ⇒ = − ω = − = − = −  
   
= −
 π π 
= − ⇒ = − ω = − = − − =  
   
=
22
2
2
2
22
2
2
2
0 0
2 2
0 5 4 93
2
4 93
2 2
0 5 4 93
2
4 93 alor máximo. El signo indica que apunta hacia la dcha)
x =Ax = - A
a= 0
v max=
m
,
s
π0 5
a max= - 4,93m/s2
v= 0v= 0
v max= -
m
,
s
π0 5
a max= 4,93 m/s2
( )v A x ; v A x A x
v x v x v
A ; A x
m
,
v s
A x
= ω − = ω − = ω − ω
+ ω + ω
= = = +
ω ω ω
= + =
ω
2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2
2 2
2 2 2
2
2
2 2
2
2
1 30
s−2 2
2
, m , m+ =2 2
0 50 0 82
a ( m
a x ; ;
x
−
= − ω ω = − ω = −2 2 / s )
, m
2
0 50
s−
= 1
2
x , sen ( t)= 0 82 2

7
Puede ocurrir que el origen de los ángulos no coincida con el de los tiempos. En este caso se debe tomar
en cuenta el ángulo descrito cuando t =0 (ángulo inicial) e incluirlo en la expresión angular de la ecuación
del MAS (que también se conoce con el nombre de "fase"). El ángulo inicial recibe el nombre de "fase
inicial" :
Algunos valores de la fase inicial:
Ejemplo 4
Determinar la ecuación de un punto que oscila con MAS de amplitud 0,80 m y frecuencia 0,5 Hz si
se empieza a contar el tiempo cuando el punto se encuentra a 0,42 m del punto de equilibrio y
moviéndose hacia la derecha:
Solución:
La fase inicial
( )ϕ0
La fase inicial se puede determinar observando
donde se encuentra el punto cuando se
comienza a contar el tiempo ( t=0). De forma
general se obtiene haciendo t =0 en la ecuación
del MAS:
x A sen ( t )
x
x A sen ( ); sen ( )
A
= ω + ϕ
= ϕ ϕ =
0
0
0 0 0
x =A
x = - A
Si el punto está en x = A
cuando t =0:
x A
sen ( )
A A
ϕ = = =
π
ϕ =
0
0
0
1
2
Si el punto está en x = - A
cuando t =0:
x A
sen ( )
A A
−
ϕ = = = −
π
ϕ =
0
0
0
1
3
2
Si el punto está en X=0 y
moviéndose hacia la derecha
cuando t=0:
ϕ = π0
Si el punto está en X=0 y
moviéndose hacia la izquierda
cuando t =0:
ϕ =0 0
x A sen ( t )
x ,
x A sen ( ); sen ( ) , ; , rad
A ,
x A sen ( f t ) , sen ( , t , ) , sen ( t , )
x , sen ( t , )
= ω + ϕ
= ϕ ϕ = = = ϕ =
= π + ϕ = π + = π +
= π +
0
0
0 0 0 0
0
0 42
0 5250 0 553
0 80
2 0 80 2 0 5 0 553 0 80 0 553
0 80 0 553

8
Ejemplo 5
Un punto que oscila con MAS de amplitud 0,20 m y 2,00 s de periodo. Si la fase inicial es de rad:
a) Escribir la ecuación que describe el movimiento.
b) Determinar la posición del punto para t=0.
c) Calcular el valor de la velocidad y aceleración al cabo de 0,50 s.
Solución:
a)
b)
c)
Ejemplo 6
Un punto oscila con MAS de amplitud 0,30 m y 1,0 Hz s de frecuencia y comienza a medirse el
tiempo cuando está en el punto de máxima elongación hacia la derecha:
a) Escribir la ecuación del movimiento
b) Calcular el valor de la velocidad cuando pase por el origen
Solución:
Como t = 0 para x = A, . La ecuación será por tanto:
b) Cuando pase por el origen x = 0:
Pasa dos veces por el origen, una hacia la derecha y otra hacia la izquierda.
π
4
x A sen ( t ) A sen ( t ) , sen (
T
π
= ω + ϕ = + ϕ =0 0
2 2
0 20
π
2
t )
x , sen ( t )
π
+
π
= π +
4
0 20
4
t
x , sen ( t )
x , sen ( ) , m=
π
= π +
π
= =0
0 20
4
0 20 0 14
4
(t , )
v A cos ( t ) A cos t , cos t , cos t
T T
v , cos , , m / s=
π π π π π π π π     
= ω ω + = + = + = π π +     
     
π 
= π π + = − 
 
0 50
2 2 2 2
0 20 0 20
4 4 2 2 4 4
0 20 0 50 0 44
4
(t , )
a A sen ( t ) A sen t , sen t , sen t
T T
m
a , sen , ,
s
=
π π π π π π π π       
= − ω ω + = − + = − + = − π π +       
       
π 
= − π π + = − 
 
2 2
2 2
2
0 50 2
2 2 4 2
0 20 0 20
4 4 4 2 4 4
0 20 0 50 1 40
4
π
ϕ =0
2
x A sen ( t )
x A sen ( f t ) , sen ( , t ) , sen ( t )
x , sen ( t )
= ω + ϕ
π π
= π + ϕ = π + = π +
π
= π +
0
02 0 30 2 1 0 0 30 2
2 2
0 30 2
2
m
v A x A f A , s , m ,
s
−
= ω − = ± ω = ± π = ± π = ± π2 2 1
2 2 1 0 0 30 0 60

1
Movimiento oscilatorio
Movimiento armónico simple (MAS)
Dinámica
IES La Magdalena.
Avilés. Asturias
La aceleración de un punto que oscila con MAS puede expresarse como:
En función del tiempo.
En función de la distancia al origen.
Por tanto, un cuerpo de masa m que oscile con MAS estará sometido a una fuerza que varía con el
tiempo en la forma:
Si elegimos como variable la distancia al origen (x) podemos expresar la fuerza actuante como:
La constante k recibe el nombre de constante elástica y se mide en N/m en el S.I.
La constante elástica en el caso de muelles permite cuantificar "la dureza" del mismo. Muelles "muy duros"
(que cuesta trabajo estirarlos) tienen una constante elástica elevada, mientras que los muelles "blandos"
(los que se estiran con facilidad) tienen constantes elásticas pequeñas.
A partir de la ecuación de definición de la constante elástica, k (ver más arriba), podemos relacionar periodo
(o frecuencia) de oscilación con k:
a x= − ω2
a A sen ( t)= − ω ω2
k m m m
T T
m
T m
k k
k
f
T mm
k
π π 
= ω = = 
 
π
= = π
= = =
π
π
2 2
2
2
2
2 4
4
2
1 1 1
2
2
F m a A m sen ( t) A k sen ( t)= = − ω ω = − ω2
Generalmente esta es la forma más usada y nos indica que en un
MAS la fuerza es proporcional al desplazamiento y opuesta a él.
Cuando el punto se coloque a la derecha del origen (en movimiento de
ida o de vuelta), la fuerza apunta hacia la izquierda; mientras que
cuando esté a la izquierda, la fuerza apunta hacia la derecha.
Es decir la fuerza apunta siempre hacia el origen (punto de equilibrio)
x =Ax = - A
F m a m x k x
Donde k m
= = − ω = −
= ω
2
2
El periodo de oscilación de un cuerpo colgado de un
resorte depende de la masa del cuerpo y de la constante
elástica del resorte. Para un mismo cuerpo el periodo será
mayor (oscilará más lentamente) cuanto menor sea la
constante elástica (cuanto "más blando" sea el muelle).
Un muelle blando producirá
un movimiento oscilatorio
con un periodo largo
(oscilación más lenta).
Un muelle duro provocará
que las oscilaciones sean
más rápidas (periodo corto)
Si se aumenta la masa del
cuerpo las oscilaciones
serán más lentas (mayor
periodo).
Una masa menor provocará
una disminución del periodo
de oscilación (oscilaciones
más rápidas) Más información en FisQuiWeb: Laboratorio
Física 2º Bachillerato, Estudio de un muelle real.

2
Ejemplo 1 (Oviedo, 2000)
Se engancha un muelle de 30 cm de longitud y constante elástica 5,0 N cm
-1
a un cuerpo de masa
2,0 kg, y el sistema se deja colgado del techo.
a) ¿En qué porcentaje se alargará el muelle?
b) Se tira ligeramente del cuerpo hacia abajo y se suelta, ¿cuál será el periodo de oscilación del
sistema?
c) Se desengancha el muelle del techo y se fija a la pared, poniendo el muelle horizontal y el
cuerpo sobre una mesa, siendo el coeficiente de rozamiento entre ambos despreciable. ¿Cuál
será el nuevo periodo de oscilación?
Solución:
El periodo de oscilación de un muelle sólo depende de la masa del cuerpo y de su constante elástica, como
ninguno de ellos varía al pasar de la posición vertical a la horizontal el periodo será el mismo.
Un bloque de 1,5 kg, colocado sobre una mesa y unido a un muelle de constante elástica k = 500
N/m, oscila sin rozamiento. La velocidad máxima que alcanza en su trayectoria es de 70 cm/s.
Calcular:
a) La frecuencia de oscilación
b) La amplitud de la oscilación
Solución:
a) El periodo de oscilación viene dado por:
La velocidad máxima se alcanza cuando el cuerpo pasa por x = 0 (ver apuntes MAS I) y tiene una
valor:
d
Cuando se cuelga el cuerpo el muelle se estira y ejerce una
fuerza elástica hacia arriba igual a kx que equilibra el peso
e eF P ; F P
, kgmg
kd mg ; d
k
− = =
= = =
0
2 0 m s−2
10
kg500 s−2
, m , cm
cm
Porcentaje :
cm
= =0 04 4 0
4
30
cm100 cm
, , %
cm cm
= =13 3 13 3
100 100
Una vez puesto en movimiento el sistema oscilará con un
periodo:
, kgm
T
k
== π = π
2 0
2 2
kg500
, s
ms−
=2
0 40
MAX
MAX
v A A f A
T
v , ms
A
f
−
π
= ω = = π
= =
π
1
2
2
0 70
2 , s−
π 1
2 2 94
, m , cm= =0 038 3 8
, kgm
T
k
== π = π
1 5
2 2
kg500
, s
ms
La frecuencia será: f , s
T , s
−
−
=
= = =
2
1
0 34
1 1
2 94
0 34
P= mg
Fe= kd

3
Podremos poner, por tanto:
Operando podemos obtener el periodo de oscilación:
En una catedral hay una lámpara que cuelga desde el techo de una nave y que se encuentra
situada a 2 m del suelo. Se observa que oscila levemente con una frecuencia de 0,1 Hz. ¿Cuál es la
altura h de la nave?
Dato. g = 9, 8 m/s
2
El péndulo simple como oscilador armónico
Cuando un péndulo oscila la fuerza que lo
impulsa es la componente del peso según la
tangente (ver fig).
Si las oscilaciones tienen mucha amplitud el
péndulo describe un arco. La trayectoria está
bastante alejada de la propia de un MAS (sobre
la recta x). El movimiento, aunque es oscilatorio,
no puede considerarse armónico simple.
Si las oscilaciones tienen poca amplitud (ver fig
de la derecha) la trayectoria seguida por el
péndulo se aproxima bastante a la propia de una
MAS, ya que entonces arco y cuerda se
confunden. Además, la fuerza puede
considerarse que apunta, con poco error, en la
dirección de la recta x.
x
x
x
F P sen mg
L
x
F mg (el signo menos indica que la fuerza se opone al desplazamiento, x)
L
Comparando con :
F k x
Concluimos :
k x
= α = −
= −
= −
x
mg=
mg
; k
L L
=
Para pequeñas oscilaciones (ángulo inferior a 20
0
) un péndulo simple
se comporta como un oscilador armónico de constante k = mg/L
mg
k ; m
L
=
m
ω =2
g
L
g L
; T
L gT
π
= = π
2
2
4
2
El periodo de un péndulo simple sólo depende de la longitud del péndulo.
Péndulos de longitudes grandes oscilaran lentamente (periodo elevado),
mientras que péndulos cortos oscilarán rápidamente (periodos cortos)
El periodo de un péndulo simple depende únicamente de su longitud, por lo
tanto para que las oscilaciones tengan una frecuencia de 0,1 Hz (T = 10 s)
la longitud del péndulo deberá de ser:
L
T
g
g , ms
L T
−
= π
= =
π
2
2
2
2
9 8
4
s
π
2 2
2
10
4
, m= 24 8
La nave tendrá, por tanto,
una altura de:
24,8 m + 2,0 m = 26,8 m2 m
h

4
La energía potencial elástica vale:
Tendrá su valor máximo en x = A y x = - A y un valor nulo en x =0
La energía cinética para un objeto que se mueva con MAS se puede escribir en función de la elongación en
la forma:
La energía cinética adquiere un valor máximo para x = 0 y nulo para x =A
Si ahora sumamos las expresiones para la energía cinética y la potencial, observamos que la suma es una
cantidad constante, lo que demuestra la interconversión de ambas formas de energía:
Estudio energético del MAS
-x
x
En la figura superior el muelle se estira hacia la
izquierda (comunicándole energía cinética). La fuerza
elástica apunta entonces hacia la derecha y realiza
trabajo negativo (restando energía cinética) que
transforma en energía potencial elástica. Si ahora se
suelta el muelle la fuerza elástica realiza trabajo positivo
y la energía potencial se transforma en cinética.
La situación es similar si el muelle se comprime (figura
inferior)
La fuerza elástica es una fuerza conservativa (ver apuntes Energía II de 1º de Bachillerato) ya que
cuando realiza trabajo negativo resta energía cinética al cuerpo que se transforma en energía potencial
elástica. La energía potencial acumulada puede volver a convertirse en energía cinética dejando que la
fuerza elástica actúe (realizando trabajo positivo)
Por ser una fuerza conservativa se cumplirá:
Ec1 + Ep1 = Ec2 + Ep2
2
p
1
E k x
2
=
( )
Ec mv
Como v A x
Ec m A x
=
= ω −
= ω −
2
2 2
2 2 2
1
2
1
2
( )
( )
Ec m A x
Ep m x
Ec Ep m A x m x m A
Ec Ep m A k A
= ω −
= ω
+ = ω − + ω = ω
+ = ω =
2 2 2
2 2
2 2 2 2 2 2 2
2 2 2
1
2
1
2
1 1 1
2 2 2
1 1
2 2

5
Ejemplo 4
Un cuerpo de 400 g oscila con MAS de ecuación:
a) Calcular los valores de la energía cinética y potencial cuando está a 0,50 y a 0,60 m del origen.
b) Comprobar que la suma de ambas energías permanece constante.
c) ¿En que punto de la trayectoria ambas energías (cinética y potencial) tendrán idéntico valor?
Según la expresión vista anteriormente la suma de la energía cinética y la potencial debe de ser constante e
igual a 1/2 k A
2
. Efectivamente:
Para saber en que punto las energía cinética y potencial tienen idéntico valor igualamos ambas:
x , sen t
,
π 
=  
 
0 60
0 60
( ) ( )
( )
A , m del origen
Ec m A x , kg s , , m , J
,
Ep m x , kg , m , J
,
Ec Ep , J , J , J
A , m del origen (x A)
Ec m A A
Ep m A , kg
−π 
= ω − = − = 
 
π 
= ω = = 
 
+ = + =
=
= ω − =
= ω =
2
2 2 2 2 2 2 2
2
2 2 2 2
2 2 2
2 2
0 50
1 1
0 400 0 60 0 50 0 603
2 2 0 60
1 1
0 400 0 50 1 371
2 2 0 60
0 603 1 371 1 974
0 60
1
0
2
1 1
0 400
2 2
, m , J
,
Ec Ep , J , J , J
π 
= 
 
+ = + =
2
2 2
0 60 1 974
0 60
0 000 1 974 1 974
Ec Ep k A m A m A , kg s , m , J
,
−π 
+ = = ω = ω = = 
 
2
2 2 2 2 2 2 2 21 1 1 1
0 400 0 60 1 974
2 2 2 2 0 60
( )
( )
( )
Ec k A x
Ep kx
Ec Ep ; k A x kx
A x x ; x A
A , m
x ; x , m
= −
=
= − =
− = =
= = =
2 2
2
2 2 2
2 2 2 2 2
1
2
1
2
1 1
2 2
2
0 60
0 424
2 2

6
Los movimientos oscilatorios reales
(por ejemplo la oscilación de un
péndulo) van perdiendo amplitud
hasta que, lentamente, se detienen
debido a la acción de fuerzas no
conservativas (rozamientos) que
convierten la energía cinética en calor.
Se dice que las oscilaciones se
amortiguan, lo que se traduce en una
disminución progresiva de la amplitud
hasta la extinción total de las
oscilaciones (ver gráfica a la derecha)
Por otro lado a un oscilador puede aplicársele una fuerza externa que lo fuerce a oscilar con determinada
frecuencia (la de la fuerza aplicada). De esta manera, debido a la acción externa, se le comunica
constantemente energía que, una vez absorbida por el oscilador, se traduce en movimiento.
La forma más efectiva de comunicar energía a un oscilador es cuando la frecuencia de la fuerza
externa coincide (aunque sea de forma aproximada) con la frecuencia natural del oscilador, que para
un muelle o un péndulo simple, viene dada por las expresiones:
Si la energía se suministra con esta frecuencia la amplitud aumenta en cada aportación pudiendo hacerse
(teóricamente) infinita, aunque en la realidad esto no llega a pasar debido a los efectos de la amortiguación
descritos más arriba.
Cuando se suministra energía a un sistema oscilante con una frecuencia igual a su frecuencia de
oscilación natural se dice que se produce resonancia, la energía del oscilador aumenta entonces en
cada aportación pudiendo adquirir valores muy altos.
El fenómeno de la resonancia es muy usado ¡incluso en la cocina! ya que los microondas funcionan según
este principio.
Un microondas tiene en su interior un dispositivo llamado magnetrón
que es capaz de generar ondas electromagnéticas (similares a las de
los dispositivos Wi-Fi) con una longitud de onda de unos 12 cm y una
frecuencia de unos 2,5 GHz. Esta es la frecuencia natural de vibración
de los enlaces O-H presentes en las moléculas de agua, grasas y
azúcares. Por esta razón estas moléculas absorben la energía
incidente provocando el calentamiento de los alimentos. Los platos y
tazas, por ejemplo, están formados por arcillas que son compuestos de
Si y O, por eso no se calientan si se introducen vacíos en su interior (si se calientan cuando introducimos en
su interior un líquido es debido a que parte del calor del líquido pasa a la taza)
Infografía sobre cómo funciona un microondas en:
http://www.consumer.es/web/es/economia_domestica/servicios-y-hogar/2004/10/04/140166.php
Oscilaciones amortiguadas y forzadas. Resonancia
Muelle
k m m ( f) ( m) f
k
f
m
= ω = π = π
=
π
2 2 2 2
2 4
1
2
Pendulo simple
L g
T ; f
g L
= π =
π
1
2
2

1
Péndulo simple, periodo y amplitud
(Ampliación)
IES La Magdalena.
Avilés. Asturias
Podremos poner, por tanto:
Operando podemos obtener el periodo de oscilación con las consideraciones hechas más arriba. Es decir,
lo que sigue sólo es válido para pequeñas oscilaciones:
Tal y como se ha dicho la ecuación anterior, que relaciona periodo y longitud de un péndulo simple, sólo es
valida para pequeñas oscilaciones. Pero... ¿cuánto de pequeñas han de ser esas oscilaciones? Podemos
dar respuesta a esta cuestión planteando una experiencia en la que midamos el periodo de un péndulo
simple para distintas amplitudes (para más información ver en FisQuiWeb, y en la sección de Laboratorio la
experiencia completa).
Cuando un péndulo oscila la fuerza que lo
impulsa es la componente del peso según la
tangente (ver fig).
Si las oscilaciones tienen mucha amplitud el
péndulo describe un arco. La trayectoria está
bastante alejada de la propia de un MAS (sobre
la recta x). El movimiento, aunque es oscilatorio,
no puede considerarse armónico simple.
Si las oscilaciones tienen poca amplitud (ver fig
de la derecha) la trayectoria seguida por el
péndulo se aproxima bastante a la propia de una
MAS, ya que entonces arco y cuerda se
confunden. Además, la fuerza puede
considerarse que apunta, con poco error, en la
dirección de la recta x.
x
x
x
F P sen mg
L
x
F mg (el signo menos indica que la fuerza se opone al desplazamiento, x)
L
Comparando con :
F k x
Concluimos :
k x
= α = −
= −
= −
x
mg=
mg
; k
L L
=
Para pequeñas oscilaciones un péndulo simple se comporta
como un oscilador armónico de constante k = mg/L
mg
k ; m
L
=
m
ω =2
g
L
g L
; T
L gT
π
= = π
2
2
4
2
El periodo de un péndulo simple sólo depende de su longitud.
Péndulos de longitudes grandes oscilaran lentamente (periodo elevado),
mientras que péndulos cortos oscilarán rápidamente (periodos cortos)

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Péndulo simple y amplitud
2
Se suministran a continuación los datos experimentales obtenidos:
Amplitud
(grados)
10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0 50,0 55,0 60,0 65,0
T (s) 1,440 1,435 1,436 1,448 1,461 1,468 1,488 1,503 1,529 1,543 1,550 1,577
La gráfica obtenida al representar periodo (T) frente a amplitud (en grados) tiene el siguiente aspecto:
La línea de puntos representa el valor del periodo calculado con la ecuación dada en la página anterior y
que sería el correspondiente a un oscilador armónico. En este caso el valor del periodo no depende de la
amplitud. Como se observa en la gráfica esto es cierto para amplitudes que no excedan de 20
0
- 25
0
. A
partir de ese valor la ecuación deducida no da resultados concordantes con la experiencia y el movimiento
oscilatorio ya no es armónico simple.
El periodo para amplitudes grandes puede calcularse a partir de una ecuación mucho más complicada:
Esta ecuación queda reducida a la anterior para valores bajos del ángulo (entonces prácticamente se
anulan los términos que contienen el seno).
Efectivamente la nueva ecuación da buenos resultados cuando se comparan los periodos calculados con
ella con los obtenidos experimentalmente. El error relativo (%) es, como máximo, del 2,35 %.
Amplitud
(grados)
10,0 15,0 20,0 25,0 30,0 35,0 40,0 45,0 50,0 55,0 60,0 65,0
T (s) Exp. 1,440 1,435 1,436 1,448 1,461 1,468 1,488 1,503 1,529 1,543 1,550 1,577
T (s) Cal. 1,421 1,425 1,429 1,436 1,443 1,452 1,463 1,475 1,489 1,505 1,522 1,541
Error (%) 1,327 0,702 0,432 0,880 1,245 1,114 1,746 1,877 2,668 2,525 1,875 2,355

1
Movimiento ondulatorio
Ondas armónicas
IES La Magdalena.
Avilés. Asturias
Una onda es una perturbación que se propaga. Con la palabra “perturbación” se quiere indicar cualquier
tipo de alteración del medio: una ondulación en una cuerda, una compresión en el aire (onda sonora),
campos electromagnéticos oscilantes (onda electromagnética)… etc.
Es muy importante diferenciar entre el movimiento que
tienen los puntos del medio cuando son alcanzados por
la onda y el movimiento de la propia onda. Los puntos
oscilan alrededor de su posición de equilibrio, mientras
que la onda se traslada hacia la derecha, por ejemplo.
Dependiendo de la distancia a la que estén situados los
puntos del medio pueden oscilar a la vez o no. Cuando
oscilan a la vez se dice que están en fase.. (ver fig.)
Se denomina longitud de onda, , la distancia mínima
existente entre dos puntos que oscilan en fase.
Dos puntos están en fase cuando están separados
una distancia igual a un número entero de longitudes
de onda:
Si no oscilan a la vez se dice que están desfasados. Un
desfase importante es el de dos puntos que oscilan de
forma tal que cuando uno está situado en una cresta el
otro lo está en un valle (ver figura). Se dice que oscilan
en oposición.
En la figura adjunta los dos puntos que oscilan en
oposición están separados por una distancia igual a
media longitud de onda:
Dos puntos oscilan en oposición cuando están
separados una distancia igual a un número impar de
semilongitudes de onda:
Clasificación según el medio de
propagación
La mayor parte de las ondas necesitan un
medio elástico que haga posible la
propagación de la perturbación de un punto
a otro. Son las llamadas ondas materiales o
mecánicas. Son ondas materiales: el sonido
(que necesita el aire para su propagación), las
ondas que se producen al agitar una cuerda
(se propagan a través de la cuerda),... etc.
Las ondas electromagnéticas, por el
contrario, no necesitan ningún medio para
propagarse. Pueden hacerlo en el vacío.
Son ondas electromagnéticas: la luz, las ondas
de radio y televisión...etc.
Clasificación según dirección de
perturbación/propagación
En las ondas transversales la dirección en
la que se produce la perturbación y la
dirección en la que se propaga son
perpendiculares. Son ejemplos de ondas
transversales las ondas electromagnéticas, la
onda que se transmite en una cuerda, las
ondas en la superficie de un lago…etc
En las ondas longitudinales la dirección de
perturbación y la de propagación es la
misma.
El sonido es una onda longitudinal.
x , , ... n∆ = λ λ λ = λ2 3
λ
x , , ... ( n )
λ λ λ λ
∆ = = +3 5 2 1
2 2 2 2
Puntos que oscilan en oposición
λ
2
La onda se propaga de izda. a dcha. Los puntos del
medio oscilan arriba y abajo al ser alcanzados por la
onda y a la vez, ya que están separados por una
distancia igual a la longitud de onda. Están en fase
λ
x , , ( n )
λ λ λ λ
∆ = = +3 5 2 1
2 2 2 2

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Movimiento ondulatorio
2
Cuando la onda se traslada una distancia igual a la longitud de onda los puntos del medio realizan una
oscilación completa.
Se denomina periodo (T) el tiempo que la onda tarda en
recorrer una distancia igual a la longitud de onda. Se
mide en segundos. También se puede definir el periodo
como el tiempo que tarda un punto en dar una oscilación
completa.
Para medir el periodo de una onda se toma como
referencia una de las crestas de la misma y se determina el
tiempo que tarda en pasar la siguiente.
Se define la frecuencia (f) como el inverso del periodo. Se mide en s
-1
o Hz (herzios)
Velocidad de propagación de una onda (v) es la rapidez con la que ésta se traslada en el medio en el
que se propaga:
Se denomina número de onda ( ) al número de oscilaciones que presenta la onda por unidad de distancia
(metro) y es la inversa de la longitud de onda. Se mide en m
-1
.
La velocidad de propagación para las ondas materiales depende de las propiedades del medio en el que se
propagan. Por ejemplo, para una
cuerda tensa depende de su
tensión y de la densidad lineal de
masa.
Las ondas electromagnéticas se propagan en el vacío (y en el aire) con una velocidad de 300 000 km/s. En
los demás medios (agua, vidrio…) se propagan más lentamente.
Amplitud (A) es el valor máximo que adquiere la
perturbación.
Para medirlo se determina el valor de la altura de una cresta
desde la línea base (la que divide en dos a la onda).
1
f
T
=
e 1
v f
t T T
λ
= = = λ = λ
A
En el sonido la frecuencia está relacionada
con el tono (agudo a grave) y la amplitud
con el volumen (débil o fuerte).
Notas Frecuencia (Hz)
Do 264
Re 297
Mi 330
Fa 354
Sol 396
La 440
Si 495
Los colores que podemos percibir son ondas
electromagnéticas de distintas frecuencias:
Color Frecuencia (valor x10
12
Hz)
Rojo 450
Naranja 475
Amarillo 515
Verde 600
Azul 650
Violeta 725
La intensidad de una luz está relacionada con la
amplitud de la onda. Una luz más intensa se
corresponde con una amplitud mayor.
λ
v
Físicamente la frecuencia se corresponde con el número
de oscilaciones que un punto realiza en un segundo.
= = µ =
µ
T m
v T Tensión ; Densidad lineal de masa:
L
%ν
% 1
ν =
λ
λ
1 m
% 11 1
2 m
0,5 m
−
ν = = =
λ

3
De todos los movimientos ondulatorios el movimiento ondulatorio armónico, u ondas armónicas, es de
especial importancia. Una onda es armónica cuando provoca en los puntos del medio un movimiento
oscilatorio armónico simple (MAS).
La ecuación de una onda armónica es:
De una manera análoga a lo visto para el MAS la fase inicial está relacionada con las condiciones
iniciales o instante en el que se comienza a contar el tiempo (t=0)
Haciendo uso de la definición de k y , y teniendo en cuenta la relación entre velocidad de propagación de
la onda, longitud de onda y periodo:
se puede escribir la ecuación anterior en otras formas alternativas:
Como puede verse la ecuación de una onda armónica es doblemente periódica. Esto es, depende
(senoidalmente) de dos variables: tiempo (t) y posición respecto del origen (x).
Para darnos cuenta de esta doble periodicidad tenemos que tener muy presente que una onda no es algo
estático, sino que se mueve (hacia la derecha, por ejemplo). Por tanto, el valor de la elongación (y) en
Ondas armónicas. Ecuación de una onda
Donde :
f
T
k
π
ω = = π
π
=
λ
2
2
2
y A sen (kx t )= ± ω + ϕ0
Valor de la
perturbación
Amplitud: valor
máximo de la
perturbación
Pulsación (s
-1
)Número de
onda (m
-1
)
Fase inicial (rad)
Signo - para ondas que se
propaguen hacia la derecha.
Signo + para ondas que se
propaguen hacia la izquierda.
ω
v
T
λ
=
x t
y A sen (kx t) A sen x t A sen
T T
x t
y A sen
T
π π   
= ± ω = ± = π ±   λ λ   
 
= π ± λ 
2 2
2
2
x t
y A sen (kx t) A sen x t A sen
T vT T
x
A sen t
T v
x x
y A sen t A sen t
T v v
π π   
= ± ω = ± = π ± =   λ   
π  
= ± 
 
π    
= ± = ω ±   
   
2 2
2
2
2

4
cualquier punto depende de no sólo del tiempo transcurrido (como ocurría en el MAS), sino de su distancia
al origen. En la figura situada debajo se muestran unas instantáneas de una onda que se desplaza hacia la
derecha tomadas a intervalos regulares de T/4 s. Si nos fijamos en uno de los puntos (el lleno, por ejemplo)
su distancia al origen es contante (cero), pero su elongación (la y) varía con el tiempo. Oscila con MAS.
Si fijamos ahora el tiempo (tomando una
instantánea de la onda) vemos que la
elongación (y) de un punto depende de su
distancia al origen (de x). En resumidas
cuentas, para saber cuál es la elongación
de un punto deberemos conocer el tiempo
y la distancia al origen.
La ecuación de una onda tiene una
doble dependencia: del tiempo y de la
distancia al origen.
Para calcular la velocidad de un punto de una onda obtenemos la derivada respecto del tiempo de la
ecuación de onda (hay que tener en cuenta que la derivada sería entonces parcial, ya que la elongación de
un punto depende de t y de x). Para calcular la aceleración obtenemos la derivada (parcial) de la velocidad
respecto del tiempo. Para una onda que se desplace hacia la derecha, se tiene:
Ejemplo 1 (Oviedo, 2006-2007)
La ecuación de una onda, expresada en unidades S I, viene dada por
Calcular su velocidad de propagación, longitud de onda, frecuencia y periodo.
Solución:
Comparando la ecuación dada con la general para una onda armónica:
t = 0 t = T/4 t = T/2 t = 3/4 T t =T
Ondas armónicas. Velocidad y aceleración
A(x,t) A sen( , x t)= −0 2 5 4
A(x,t) A sen( , x t)
y A sen(kx t)
Deducimos que :
A A (m)
k , m
s
−
−
= −
= − ω
=
=
ω =
0
0
1
1
2 5 4
2 5
4
K ; , (m) , m
k , m
; T (s) , s
T s
f s , s
T (s)
, m m
v ,
T s
s
−
−
− −
π π π
= λ = = = π =
λ
π π π π
ω = = = = =
ω
= = = =
π π
λ π
= = =
π
1
1
1 1
2 2 2
0 8 2 51
2 5
2 2 2
1 57
24
1 1 2
0 64
2
0 8
1 60
2
x
x
y A sen (kx t )
dy y
v A cos (kx t )
dt t
dv v
a A sen (kx t )
dt t
= − ω + ϕ
δ 
= = = − ω − ω + ϕ  δ 
δ 
= = = − ω − ω + ϕ  δ 
0
0
2
0
v A y
a y
= ω −
= − ω
2 2
2
Podemos también realizar estos cálculos
teniendo en cuenta que los puntos se mueven
con MAS y que su velocidad y aceleración
vienen dados por (recordar que el movimiento
tiene lugar según el eje Y):

5
Una onda armónica transversal que se propaga en una cuerda viene dada (en unidades SI) por :
Calcular:
a) Su velocidad de propagación
b) ¿Cuál es la velocidad máxima de cualquier partícula (o segmento infinitesimal) de la cuerda?
Solución:
a) Comparando la ecuación dada con la general para una onda armónica:
b) Todos los puntos de la cuerda vibran con MAS y adquirirán su máxima velocidad cuando pasen
por el punto de equilibrio (y=0). La velocidad máxima para un punto que oscile con MAS (ver
apuntes) viene dada por:
Para calcular la fase inicial haremos uso de las ecuaciones que nos dan la elongación y la velocidad.
Suponemos que la onda viaja hacia la derecha:
Dando valores a la fase inicial obtenemos los valores correspondientes para y (elongación) y v (velocidad):
y v
0 0
A 0
0
- A 0
y(x,t) , sen( , x , t)= −0 02 2 5 3 2
y(x,t) , sen( , x , t)
y A sen(kx t)
Deducimos que :
A , m
k , m
, s
−
−
= −
= − ω
=
=
ω =
1
1
0 02 2 5 3 2
0 02
2 5
3 2
K ; , (m) , m
k , m
; T , (s) , s
T , s
, m m
v ,
T , (s) s
−
−
π π π
= λ = = = π =
λ
π π π
ω = = = = π =
ω
λ π
= = =
π
1
1
2 2 2
0 8 2 51
2 5
2 2 2
0 0625 1 96
3 2
0 8
1 28
0 0625
v A Donde los signos indican el sentido
m cm
v , s . , m , ,
s s
−
= ± ω
= = =1
3 2 0 02 0 064 6 4
La fase inicial
ϕ0
A− ω
π
2
π Aω
π3
2
y A sen (kx t )
v A cos (kx t )
= − ω + ϕ
= − ω − ω + ϕ
0
0
( )y , A sen ( )
v( , ) A cos ( )
= ϕ
= − ω ϕ
0
0
0 0
0 0
En el instante t=0 y para x =0, tendremos:
y A sen (kx t)= − ω y A sen (kx t )
π
= − ω +
2
y A sen (kx t )= − ω + π y A sen (kx t )= − ω + π
3
2
Se muestran a continuación el aspecto y la ecuación de varias ondas que
se mueven hacia la derecha y tienen distinta fase inicial.
NOTA
Las ecuaciones anteriores pueden servirnos para calcular el desfase, ya que:
0 0
0 0ϕ = ϕ = −
ω
y v
sen ( ) cos ( )
A A

6
NOTA
Cuando la fase vale , y teniendo en cuenta que , podemos escribir:
Cuando la fase vale , y teniendo en cuenta que , podemos escribir:
Dos puntos de una onda oscilan en fase cuando están en idéntico estado de movimiento. Por ejemplo
si en un instante dado ambos están en una cresta de la onda.
Dos puntos oscilarán en fase (ver pag 1) cuando estén separados por una distancia igual a un número
entero de longitudes de onda:
Dos puntos se dice que están en oposición si su estado de movimiento es opuesto, es decir sus
velocidades tienen idéntico valor, pero se mueven en sentido contrario. Esto sucede, por ejemplo, cuando
uno de los puntos está en una cresta y otro en un valle.
El desfase entre dos puntos, en consecuencia, depende de la distancia entre ambos y podremos calcularlo
restando las fases (ángulo) de la ecuación de onda correspondiente.
Si imaginamos dos puntos de una misma onda situados a una distancia x1 y x2 del origen, en un instante
dado (t), tendrán una elongación (y) dada por:
La diferencia de las fases de ambos (desfase) valdrá:
π sen( ) sen( )α + π = −α
y A sen (kx t ) A sen (kx t) A sen ( t kx)= − ω + π = − − ω = ω −  
x , , ... n∆ = λ λ λ = λ2 3
x , , ... ( n )
λ λ λ λ
∆ = = +3 5 2 1
2 2 2 2
Puntos oscilando en fase Puntos oscilando en oposición
λλ λ
2
y A sen (kx t )
y A sen (kx t )
= − ω + ϕ
= − ω + ϕ
1 1 0
2 2 0
π
2
y A sen (kx t ) A cos (kx t)
π
= − ω + = − ω
2
sen( ) cos( )
π
α + = α
2
El problema del desfase
(kx t ) (kx t ) kx kx
k(x x ) k x
∆ϕ = − ω + ϕ − − ω + ϕ = −
∆ϕ = − = ∆
2 0 1 0 2 1
2 1

7
Si los puntos considerados están separados por una distancia igual a un múltiplo entero de longitudes de
onda estarán en fase, y si lo están por un número impar de semilongitudes de onda lo harán en oposición.
Por tanto:
El concepto de desfase podemos extenderlo a dos ondas.
En la figura de más abajo pueden verse dos ondas ( ) con desfases diferentes. Las de la figura
de la izquierda están desfasadas ( lo que se corresponde con una ). Las ondas de la
figura de la derecha están desfasadas
Ejemplo 3
Para la onda de ecuación determinar:
a) ¿Cuál será el desfase entre dos puntos situados a 4 m de distancia?
b) ¿Cuál será el desfase entre dos puntos situados a 6 m de distancia?
c) ¿Cuál será el desfase entre dos puntos situados a 5,6 m de distancia?
Solución:
a) De la ecuación podemos deducir la longitud de onda:
Por tanto, los dos puntos separados 4 m estarán en fase (idéntico estado de movimiento)
b) De lo dicho en el apartado anterior se deduce que dos puntos situados a 6 m oscilarán en
oposición, ya que 6 m es la distancia correspondiente a tres semilongitudes de onda.
c) Dos puntos separados 5,6 m no oscilaran ni en fase ni en oposición. El desfase, en este
caso, es intermedio entre ambas situaciones y vale:
/π 6
, mλ = 12 0
x , m∆ = 1 0
/π 2
y(x,t) sen( x t)
π
= − π2 5
2
k ; m
k
π π π
= λ = = =
πλ
2 2 2
4
2
,
k x m , m ,−π
∆ϕ = ∆ = = π = π1 5 6
5 6 2 8
2 2
Para dos puntos en fase :
k x k n
π
∆ϕ = ∆ = λ =
λ
2
n λ n
Para dos puntos en oposición :
k x k ( n )
= π
λ
∆ϕ = ∆ = + =
2
2
2 1
2
π
λ
( n )
λ
+2 1
2
( n )= + π2 1
Situación (aproximada) de dos
puntos desfasados 2,8 π ó 5,6 m

8
Una de las características más sobresalientes (y útiles) del movimiento ondulatorio es que las ondas
transportan energía de un punto a otro sin que exista transporte de masa. Si la onda es armónica los puntos
del medio oscilan con MAS y su energía será la suma de la energía cinética y la potencial :
A partir de aquí se puede establecer una relación entre la energía que una onda transfiere a los puntos del
medio y sus parámetros característicos, tales como la frecuencia:
La energía transferida por una onda a un punto del medio en el que se propaga depende del cuadrado de
su frecuencia y del cuadrado de su amplitud.
La frecuencia es una característica de las ondas. En la tabla adjunta se proporciona la frecuencia de
algunas ondas electromagnéticas conocidas.
Ondas
(electromagnéticas)
Frecuencia (Hz)
Rayos gamma 10
20
(100 EHz)
Rayos X 10
18
(EHz)
Luz visible 10
14
(100 THz)
Microondas 10
9
(GHz)
Ondas de radio 10
6
(MHz)
Hz Abreviatura Nombre
10
21
ZHz Zettahercio
10
18
EHz Exahercio
10
15
PHz Petahercio
10
12
THz Terahercio
10
9
GHz Gigahercio
10
6
MHz Megaherzio
Como se ve la energía que los rayos X pueden transferir a los cuerpos sobre los que incidan es muy
superior a la de las microondas, por ejemplo, y esa es una de las causas de la peligrosidad que presenta la
exposición a radiaciones de alta frecuencia.
La amplitud está relacionada con la intensidad de la onda. De tal manera que para una onda de
determinada frecuencia la energía transferida es tanto mayor cuanto mayor es su intensidad. La intensidad
de una onda se atenúa muy rápidamente a medida que nos alejamos del foco emisor. De ahí que las
consecuencias para la salud serán más graves si estamos próximos al foco emisor de las mismas (antenas
de telefonía móvil u otro tipo de emisores).
El sonido también es una onda. En este caso, los efectos nocivos para la salud pueden provenir más de su
elevada intensidad (volumen elevado), que de su frecuencia, ya que los sonidos audibles para el oído
humano tienen frecuencias moderadas, situadas entre los 20 y los 20 000 Hz.
Energía asociada a una onda
cin potE E E k A= + = 21
2
( )E k A m A m f A m f A= = ω = π = π2 2 2 2 2 2 2 2 21 1 1
4 2
2 2 2

1
Propagación de las ondas
Fenómenos ondulatorios
IES La Magdalena.
Avilés. Asturias
Cuando se trata de visualizar la propagación de las ondas en un papel se recurre a pintar los llamados
frentes de onda. Esto es, líneas continuas que unen todos los puntos de la onda que están en fase,
por ejemplo las crestas. Se dibujan a continuación los frentes de una onda plana y otra circular:
También resulta muy cómodo (y muy visual) pintar los rayos, unas líneas perpendiculares a los frentes
de onda.
Christian Huygens (1629-1695) propuso hacia 1680 un
método gráfico que permite obtener los frentes de onda
sucesivos de una onda que se propaga.
Huygens consideraba que cuando la perturbación que
constituye la onda alcanza los puntos del medio, éstos se
convierten en fuentes secundarias de ondas y se puede
obtener el nuevo frente de ondas trazando la envolvente
de las ondas secundarias emitidas (Principio de Huygens).
El proceso se puede repetir, con lo que podemos seguir la
propagación de la onda a través del medio.
En el modelo de Huygens se ignoran las ondas emitidas en
sentido contario al de propagación
El modelo de Huygens fue perfeccionado posteriormente por
Kirchhoff quien introdujo una descripción matemática más
rigurosa.
.
Frentes de ondas planas. Las
líneas de puntos unen puntos de
máxima amplitud (crestas)
Frentes de ondas circulares. Las
líneas llenas unen puntos de
máxima amplitud (crestas)
Frentes de onda y rayos. El sentido de la propagación se indica con una flecha
Envolvente nuevo
frente de onda
Ondas
secundarias

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Propagación y fenómenos ondulatorios
2
La difracción de las ondas constituye un fenómeno característico de éstas, hasta el punto que fue
usado como prueba de la naturaleza ondulatoria de los electrones.
La difracción tiene lugar cuando las ondas que se propagan encuentran un obstáculo, por ejemplo un
orificio, cuyas dimensiones son del orden de la longitud de onda de las ondas incidentes. Las ondas se
propagan entonces como si el orificio se convirtiera en un nuevo centro emisor y penetran tras el orificio en
lo que debería de ser una "zona de sombra" si su comportamiento fuera como el de un chorro de partículas.
Según Huygens este comportamiento puede explicarse si suponemos que el propio orificio se convierte en
una fuente secundaria de ondas.
Si la onda incidente es plana la que emerge del orificio es una
onda circular.
La onda difractada tiene la misma amplitud, frecuencia y longitud
que la onda incidente.
Difracción de las ondas
Si el orificio es de un tamaño
similar a la longitud de onda (o
menor) las ondas se difractan y
se propagan detrás de él. Este
fenómeno puede explicarse
suponiendo que el orificio se
convierte en una fuente
secundaria de ondas (Principio
de Huygens).
Si el orificio es mayor que la
longitud de onda no hay
difracción. Tras el obstáculo
aparece una zona en la que
no se propagan las ondas.
A la derecha se muestra la difracción de
un onda por un obstáculo interpuesto en
su trayectoria. Los frentes de onda se
curvan en sus bordes según lo predicho
por el Principio de Huygens.

3
La interferencia entre dos ondas tiene lugar cuando ambas coinciden en una región del espacio al mismo
tiempo. Cuando esto sucede ambas se suman (principio de superposición) produciendo una onda resultante
El fenómeno de la interferencia es algo característico del movimiento ondulatorio.
La interferencia se produce únicamente en los puntos en que ambas ondas coinciden. Si, por ejemplo,
ambas se desplazan en sentidos contrarios interferirán cuando se encuentren y después ambas ondas
siguen su camino sin sufrir alteración.
Matemáticamente la onda resultante se obtiene como suma de las ecuaciones de las ondas incidentes:
La onda resultante puede ser complicada (ver hoja de cálculo), aunque existen algunos casos sencillos que
conviene tener en cuenta:
• Ondas con la misma frecuencia y longitud de onda (ondas coherentes)
Si la fase es idéntica se produce lo que se llama
interferencia constructiva. Las amplitudes de
ambas ondas se suman : A = A1 + A2.. Esto sucede
cuando la diferencia entre las fases sea:
En la figura de la izquierda pueden verse dos ondas
(líneas de puntos) con idéntica fase y distinta amplitud
en interferencia constructiva. La resultante se indica
con línea llena. Su amplitud es la suma de las
amplitudes de las ondas.
Para la figura:
Si las ondas están en oposición se produce lo que
se llama interferencia destructiva Las amplitudes
de ambas ondas se restan : A = A1 - A2. Si A1 = A2 la
onda resultante tiene una amplitud nula (se
produce la extinción). Esto sucede cuando la
diferencia en fase sea:
En la figura de la izquierda pueden verse las dos ondas
anteriores (líneas de puntos), pero ahora con una
diferencia de fase de rad (interferencia destructiva).
Interferencia
A la izquierda: ondas propagándose en sentidos contrarios
En el centro: las ondas (líneas de puntos) coinciden produciéndose interferencia (resultante con línea llena)
Derecha: las ondas siguen su camino inalteradas
y A sen (k x t )
y A sen (k x t )
y y y A sen (k x t ) A sen (k x t )
= ± ω + ϕ
= ± ω + ϕ
= + = ± ω + ϕ + ± ω + ϕ
1 1 1 1 1
2 2 2 2 2
1 2 1 1 1 1 2 2 2 2
y , sen ( , x t)
y , sen ( , x t)
= − π
= − π
1
2
1 50 1 26
2 00 1 26
π
n (n , , ...)∆ϕ = π =2 0 1 2
( )n (n , , ...)∆ϕ = + π =2 1 0 1 2

4
• Ondas con distinta frecuencia y longitud de onda.
La onda resultante de la interferencia (tal y como se ha dicho más arriba) puede ser complicada.
Se produce un fenómeno curioso cuando interfieren ondas de frecuencia muy próximas. Entonces la
amplitud de la onda resultante varía periódicamente con el tiempo produciendo máximos y mínimos de
amplitud que reciben el nombre de pulsaciones. Se dice que la amplitud está modulada (ondas AM)
En la figura de la izquierda se pueden observar las
pulsaciones surgidas como consecuencia de la
interferencia de dos ondas de idéntica amplitud que se
propagan con velocidad de 10 m/s y cuyas frecuencias,
muy próximas, son 80 s
-1
y 82 s
-1
.
Las pulsaciones se pueden escuchar produciendo
sonidos de frecuencias próximas. Se perciben entonces
las subidas periódicas de volumen (relacionadas con la
amplitud). Esto es un efecto que los músicos usan para
afinar sus instrumentos. Si la frecuencia del instrumento
no es la misma que la que se da como referencia para
el afinado se escucharán batidos (pulsaciones) que
desaparecen cuando las frecuencias se igualan. El
instrumento estará entonces afinado.
Debajo se muestra el fenómeno de interferencia producido por una doble rendija. Cada rendija se convierte
en un foco secundario de una ondas idénticas y ambas interfieren formando un patrón típico. Con puntos
se señalan en el dibujo las zonas en las que existe interferencia constructiva (líneas ventrales). Entre
ambas se sitúan las zonas de interferencia destructiva (líneas nodales). A la derecha se muestra una foto
de una cubeta de ondas en la que se observa realmente el fenómeno. Se identifican fácilmente las líneas
ventrales y nodales
En este caso la interferencia se produce debido a la diferente
distancia recorrida por las ondas procedentes de ambas rendijas.
En las zonas en las que la diferencia de distancia recorrida es un
múltiplo entero de longitudes de onda se produce interferencia
constructiva. Las ondas llegan en fase.
En las zonas en las que la diferencia de distancia recorrida es un
múltiplo de media longitud de onda se produce interferencia
destructiva. Las ondas llegan en oposición.
Línea de
interferencia
constructiva
(línea ventral)
Línea de
interferencia
destructiva
(línea nodal)

5
Muy frecuentemente el plano en el
que se produce la perturbación en
una onda transversal no es único
y, entonces, las oscilaciones se
localizan en varios planos.
Es posible, mediante algunos
procedimientos (ver más abajo),
"filtrar" la onda de forma que se
seleccione un único plano de
oscilación. La onda resultante se
dice que está polarizada ya que
en ella la oscilación tiene lugar
en un único plano.
La polarización es una propiedad especialmente importante en el caso de ondas electromagnéticas.
En las ondas electromagnéticas la perturbación que se propaga son campos eléctricos (E) y magnéticos (B)
que forman entre sí 90
0.
El valor estos campos en un punto oscila entre los valores máximo y mínimo.
Para fijar el plano de oscilación de la
perturbación se toma como referencia el
plano de oscilación del campo eléctrico.
En una onda electromagnética polarizada,
por tanto, el plano de oscilación del
campo eléctrico es siempre el mismo.
Existen algunas sustancias, llamadas
polarizadores, que cuando una onda
electromagnética (por ejemplo la luz) las
atraviesa sólo dejan pasar aquellas ondas
en las que el plano de oscilación del campo
eléctrico tiene una dirección determinada. La
luz que emerge de la sustancia estará
polarizada.
Si a continuación se sitúa otro polarizador
cruzado (que forme 90
0
con el primero) la luz
no pasará, demostrando la polarización de
la luz incidente sobre él.
Otras sustancias, por ejemplo la glucosa, tienen la propiedad de que cuando se hace pasar luz polarizada a
través de ellas son capaces de girar el plano de polarización de la luz. Estas sustancias se dice que son
ópticamente activas, y la desviación del plano de polarización permite clasificarlas en sustancias
dextrógiras si desvían el plano de polarización hacia la derecha o levógiras si lo desvían hacia la
izquierda.
Polarización
Arriba onda transversal en la que la perturbación transmitida se
localiza en dos planos perpendiculares. No está polarizada.
Abajo onda transversal polarizada. La oscilación se produce sólo
en el plano vertical.
Luz incidente.
No polarizada
Polarizador
Luz polarizada
Polarizador
cruzado
(analizador)

6
El llamado efecto Doppler (en honor del matemático austriaco Andreas Doppler, que lo descubrió en 1842)
consiste en el cambio de frecuencia percibido por un observador cuando se mueve respecto de la
fuente que emite las ondas. La explicación cualitativa del efecto puede verse en la figura situada bajo
este párrafo en el que se supone que la onda es el sonido emitido por el megáfono.
Cuando la fuente se acerca al observador en reposo (el efecto sería el mismo si es el observador el que se
acerca a la fuente) los frentes de onda emitidos aparecen llegan al observador más juntos como
consecuencia del movimiento y éste percibe un sonido de mayor frecuencia que la realmente emitida.
El efecto contrario se observa cuando el observador y la fuente se alejan el uno del otro. El observador
percibe un sonido de menor frecuencia que el emitido
La ecuación que aparece junto a la figura permite calcular la frecuencia percibida por el observador.
Ejemplo 1
Si el megáfono emite un sonido de 440 Hz (La) y se aproxima al observador a una velocidad de 40
m/s ¿Cuál será la frecuencia percibida por éste?
Solución:
Tomando como velocidad del sonido 340 m/s y considerando el origen situado en el observador y
positivo hacia la derecha:
f = 440 Hz ; v= 340 m/s ; v0 =0 ; vF = 40 m/s
El efecto Doppler permitió a Edwin Hubble en 1929 afirmar que las galaxias no estaban quietas y la
mayoría se movían alejándose de nosotros con una velocidad directamente proporcional a la distancia que
nos separa de ellas. El universo no es estático.
Hubble llegó a esta conclusión estudiando el
espectro de la luz proveniente de las galaxias.
Analizando dichos espectros observó que algunas
líneas conocidas aparecían a una frecuencia menor de
la esperada (mostraban un "corrimiento hacia el
rojo"), lo que significaba, según el efecto Doppler, que
la fuente emisora (la galaxia) se aleja de nosotros.
Conociendo el valor del incremento de la frecuencia
correspondiente puede establecerse la velocidad con
que se alejan. Hubble dedujo que esta velocidad
(velocidad de recesión) era proporcional a la distancia. Esto es, cuanto más lejos está una galaxia, más
rápidamente se aleja de nosotros.
Efecto Doppler
m / s
f Hz=0
340
440
( )
m
s
−
−
0
340 40
m
,
s
= 498 7 El observador percibe una frecuencia
que es prácticamente un Si
f
Imagen en la que se observa el corrimiento hacia
el rojo (imagen superior) de las líneas espectrales

1
Ondas estacionarias IES La Magdalena.
Avilés. Asturias
Un caso interesante de interferencia de ondas surge cuando interfieren dos ondas idénticas que se
propagan en sentidos contrarios (lo que sucede, por ejemplo, cuando la onda reflejada y la incidente se
encuentran). Podemos obtener la onda resultante realizando la suma de las ondas que interfieren:
El análisis del resultado obtenido nos muestra que hemos obtenido la ecuación de un MAS en el que la
amplitud depende de la distancia al origen (x):
La onda resultante de la interferencia hace que los puntos vibren arriba y abajo, unos con mayor amplitud,
otros con menor, algunos con amplitud nula, pero en situación estacionaria. La energía no se transmite de
unos a otros como en las ondas. Por eso la onda resultante recibe el nombre de onda estacionaria.
Los puntos de amplitud nula reciben el nombre de nodos y estarán situados a una distancia de:
y A sen (kx t)
y A sen (kx t)
y y y A sen (kx t) sen (kx t) ( )
Si hacemos : kx t y kx t
Y teniendo en cuenta que :
sen sen sen cos
Tenemos :
kx t
sen (kx t) sen (kx t) sen
= − ω
= + ω
= + = − ω + + ω  
α = − ω β = + ω
α + β α − β
α + β =
− ω
− ω + + ω =
1
2
1 2 1
2
2 2
2
kx t+ + ω kx
cos
2
t kx− ω − t
sen
− ω
=
=
2
2
2
kx
2
cos
− 2 tω
2
( ) ( )
( ) ( )
( ) ( )
( ) ( )
sen kx cos t
Y teniendo en cuenta que : cos cos
sen (kx t) sen (kx t) sen kx cos t
Sustituyendo en ( ):
y y y A sen kx cos t
= − ω
α = −α
− ω + + ω = ω
= + = ω1 2
2
2
1
2
R
R
y A sen(kx) cos( t) A cos( t)
Donde A A sen(kx)
= ω = ω
=
2
2
RA A sen(kx)
sen (kx)
kx , , ... n
kx n
= =
=
= π π π
= π
π
2 0
0
0 2
2
x n= π
λ
x n
λ
=
2
Los nodos de una onda estacionaria se localizan a distancias
iguales a un número entero de semilongitudes de onda.

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Ondas estacionarias
2
La amplitud tendrá su valor máximo (vientre) cuando el seno adquiera su valor máximo:
Observar que la onda correspondiente a la ecuación tiene un nodo en el, origen (x =0)
NOTA
En algunos textos se da como ecuación para las ondas estacionarias la siguiente:
Esta ecuación se corresponde con una onda estacionaria que tiene un vientre en el origen (x=0), ya que en
este punto la amplitud vale 2A:
Observar (ver figura)
que en este caso los
vientres se localizan a
una distancia igual a
un número entero de
semilongitudes de
onda y los nodos a un
número impar de
cuartos de la longitud
de onda.
( )
( )
sen (kx)
kx , , ... n
kx n
= ±
π π π π
= +
π
= +
π
1
3 3 2 1
2 2 2 2
2 1
2
2
( )x n
π
= +
λ
2 1
( )x n
λ
= +
2
2 1
4
Los vientres de una onda estacionaria se localizan a distancias
iguales a un número impar de cuartos de la longitud de onda.
y A cos(kx) sen( t)= ω2
y A cos(kx) sen( t)= ω2
Para x=0, cos 0 = 1, AR = 2 A
y A sen(kx) cos( t)= ω2
Para x=0, sen 0 = 0, AR =0
Distancia entre dos nodos:
Distancia entre dos vientres:
Distancia nodo-vientre:
λ
2
λ
2
λ
4

3
Un caso muy corriente de aparición de ondas estacionarias son las cuerdas vibrantes o las columnas de
aire confinadas en tubos.
En estos casos existe una restricción importante impuesta por las condiciones físicas en los extremos de la
onda (condiciones de contorno).
• Cuerda fija en ambos extremos o tubo cerrado
Debido a que en los extremos debe existir un nodo no son posibles todas las ondas, debe cumplirse
que la longitud de la cuerda o el tubo sea igual a un número entero de semilongitudes de onda:
Condición para que se forme la onda: Donde n = 1, 2, 3...
El primer modo de vibración se obtiene para n = 1 y se denomina modo fundamental o primer armónico.
Para n =2 tenemos el segundo modo de vibración o segundo armónico. Tiene un nodo en el centro.
Observar que la frecuencia de la onda es doble en este modo (long. de onda, mitad que la fundamental)
Para n =3 tenemos el tercer modo de vibración o tercer armónico. Tiene dos nodos. Observar que la
frecuencia de la onda es triple en este modo (long. de onda, un tercio de la fundamental).
Las frecuencias de los armónicos son doble, triple...etc. de la fundamental.
En los instrumentos de cuerda: violín, guitarra, violoncello o piano se producen este tipo de ondas al pulsar
las cuerdas
• Cuerda libre en ambos extremos o tubo abierto en ambos extremos
Ahora debe de existir un vientre en ambos extremos, luego las únicas ondas posibles son aquellas para
las que la longitud de la cuerda o tubo sea igual a un número entero de semilongitudes de onda
Condición para que se forme la onda: Donde n = 1, 2, 3 ...
Ahora el primer modo de vibración (modo fundamental o primer armónico) tiene un nodo (en el centro), el
segundo armónico dos...etc. La flauta dulce produce este tipo de ondas.
Las frecuencias de los armónicos son doble, triple...etc. de la fundamental.
Ondas estacionarias en cuerdas vibrantes y en tubos
L n ; L
n
λ
= λ =
2
2
L n ; L
n
λ
= λ =
2
2

4
• Cuerda fija en uno de sus extremos y libre en el otro o tubo abierto en uno de sus extremos
Ahora debe de cumplirse que exista un nodo en el extremo fijo y un vientre en el libre, luego las únicas
ondas posibles son aquellas que cumplan que la longitud de la cuerda o tubo sea un múltiplo impar de
cuartos de la longitud de onda.
Condición para que se forme la onda:
Condición para que se forme la onda: Donde n = 1, 3, 5 ...
El primer modo de vibración (modo fundamental o primer armónico) se obtiene para n=1
Para n =3 tenemos el tercer modo de vibración o tercer armónico. Tiene un nodo a 2/3 de L Observar que
la frecuencia de la onda es el triple de la fundamental en este modo (long. de onda, un tercio de la
fundamental)
Para n =5 tenemos el quinto modo de vibración o quinto armónico. Tiene dos nodos (a 2/5 y 4/5 de L).
Observar que la frecuencia de la onda es cinco veces mayor en este modo (long. de onda, un quinto de la
fundamental)
Observar que en este caso se encuentran ausentes los armónicos pares.
Los armónicos tienen una frecuencia triple, quíntuple... etc. de la fundamental.
Los instrumentos llamados "de embocadura" como el clarinete o el oboe producen este tipo de ondas.
Ejemplo 1. (Oviedo, 2010-2011)
Realice un dibujo del cuarto armónico de una onda estacionaria en una cuerda de piano sujeta por
ambos extremos.
a) Si la longitud de la cuerda es de 100 cm, cuánto vale la longitud de onda?
b) Si la frecuencia generada por este cuarto armónico es de 925 Hz, ¿cuánto vale la velocidad
de propagación?
c) Cuánto vale la frecuencia del primer armónico?
Solución:
a) Se muestran a continuación los cuatro primeros modos de vibración para una cuerda que vibra
con los extremos fijos:
Como se ve para una cuerda con los extremos fijos todos los armónicos han de cumplir la condición
de contorno de que en los extremos existan nodos. Para el cuarto modo su longitud de onda es
un cuarto de la del modo fundamental y, en consecuencia, su frecuencia será cuatro veces superior
a la frecuencia fundamental.
L n ; L
n
λ
= λ =
4
4
L n ; L
n
λ
= λ =
2
2
Para una cuerda sujeta por ambos extremos se tiene:
Por tanto para el cuarto modo de vibración : L , m , m
n
λ = = =
2 2
1 00 0 50
4

5
b)
c) Tal y como se explica más arriba el primer armónico tienen una longitud de onda cuatro veces
superior a la del cuarto, por tanto su frecuencia será cuatro veces menor:
f (1er armónico, frecuencia fundamental) = 231,3 Hz
Ejemplo 2. (Oviedo, 2008-2009)
Una onda estacionaria en una cuerda tensa tiene por función de ondas:
Determine:
a) La localización de todos los nodos en
b) El periodo del movimiento de un punto cualquiera de la cuerda diferente de un nodo.
c) La velocidad de propagación de la onda en la cuerda.
Solución:
a) Escribamos primero la ecuación de onda (en unidades S.I) de una manera más adecuada, ya
que la introducción de las unidades en una ecuación (donde ya existen números y letras) dificulta
su lectura:
Una onda estacionaria se caracteriza por tener una determinada amplitud función de la distancia al
origen y que los diversos puntos oscilan con MAS dando lugar a una situación estacionaria.
La ecuación dada no está correctamente escrita (al menos sus términos están desordenados).
Debería de haberse escrito en la forma:
Ahora observamos claramente que para x = 0, AR = 0.
El esquema para la onda
estacionaria considerada será pues:
Por tanto, entre 0 y 0,40 m existen
tres nodos: uno en el origen, otro a
0,20 m (media longitud de onda) y un tercero al final, a 0,40 m (una longitud de onda)
b) Como se ha dicho más arriba todos los puntos oscilan con MAS de idéntico periodo (aunque
diferente amplitud).
c)
m
v f , m . s ,
s
−
= λ = =1
0 50 925 462 5
y , m cos( s t) sen( , m x)− −
= π π1 1
0 040 40 5 0
x , m≤ ≤0 0 40
y , cos( t) sen( , x)= π π0 040 40 5 0
R
y , sen( , x) cos( t)
Donde : A , sen( , x)
= π π
= π
0 040 5 0 40
0 040 5 0
Como k
, m
k
π
= = π
λ
π π
λ = = =
π
2
5
2 2
0 4
5
R
y , sen( , x) cos( t)
y A cos( t)
Por tanto : ; T
T
= π π
= π
π π
ω = = π =
0 040 5 0 40
40
2 2
40
π40
, s= 0 05
, m m
v ,
T , s s
λ
= = =
0 40
8 00
0 05

1
Ondas estacionarias en una cuerda
sujeta por ambos extremos
Ampliación
IES La Magdalena.
Avilés. Asturias
Cuando se estudian las ondas estacionarias en una cuerda (no flexible) sujeta por ambos extremos
debemos de tener en cuenta tres ecuaciones fundamentales:
• La que da la velocidad de propagación para cualquier onda:
• La que nos da la velocidad de propagación de una onda en una cuerda tensa (depende de la tensión
y de la densidad lineal: kg/m):
• La que impone las condiciones de contorno para que pueda existir la onda. Esto es, que exista un
nodo en cada extremo:
Combinando las tres obtenemos la ecuación que ha de satisfacerse para que exista onda en la cuerda:
(1)
Hay, por tanto, cuatro parámetros que podemos manejar a la hora de plantearnos la producción de
ondas estacionarias en una cuerda: L, T, µ y f.
1. Mantenemos fija la cuerda (µ), su tensión (T) y la frecuencia (f), haciendo oscilar la cuerda
con la frecuencia propia de un oscilador externo.
En este caso para que se satisfaga la ecuación (1) deberemos variar la longitud de la cuerda.
Con n =1 obtendremos el primer modo de vibración, primer armónico o modo fundamental. Para
n = 2 obtenemos el segundo modo de vibración o segundo armónico; para n = 3 el tercer modo
de vibración o tercer armónico... etc
En este caso todos los armónicos tienen la misma longitud de onda.
v f= λ
T
v =
µ
L n
2
λ
=
T
L n
2 f
µ
=

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Ondas estacionarias en una cuerda
2
2. Mantenemos fija la cuerda (µ), su longitud (L) y la frecuencia (f), haciendo oscilar la cuerda
con la frecuencia propia de un oscilador externo.
En este caso para que se satisfaga la ecuación (1) deberemos variar la tensión de la cuerda.
de vibración o tercer armónico... etc.
Como se puede observar en el esquema hay que disminuir la tensión (de arriba a abajo) para
que aparezcan los correspondientes armónicos.
Al variar la tensión variará la velocidad de la onda y, al mantener constante la frecuencia de
oscilación, variará la longitud de onda de la onda estacionaria. A menor tensión, menor
velocidad de propagación y, como la frecuencia se mantiene constante, disminuirá la longitud de
onda. Esto es lo que se aprecia en el esquema anterior al ir de arriba (mayor tensión, mayor
velocidad, mayor longitud de onda) a abajo( (menor tensión, menor velocidad, menor longitud
de onda).
3. Mantenemos fija la tensión de la cuerda (T), su longitud (L) y la frecuencia (f), haciendo
oscilar la cuerda con la frecuencia propia de un oscilador externo.
En este caso para que se satisfaga la ecuación (1) deberemos variar la propia cuerda de tal
forma que su densidad lineal satisfaga la ecuación:
de vibración o tercer armónico... etc.
Para comprobar esto experimentalmente lo más operativo es usar diversas cuerdas, determinar
su densidad lineal de masa y comprobar que se cumple la ecuación (1) variando la longitud en
cada caso.
Al variar las cuerdas variará la velocidad de propagación de la onda:
2
2 2
T
n
4 L f
µ =
T
v =
µ

3
En cuerdas más ligeras (menor densidad lineal) la velocidad de propagación será mayor y en
cuerdas más pesadas (mayor densidad lineal) la velocidad de propagación será menor. Si
mantenemos constante la frecuencia de oscilación (mediante un oscilador externo)
comprobaremos que la longitud de onda es mayor para cuerdas más ligeras y más grande para
cuerdas más pesadas.
Los instrumentos de cuerda: violoncello, violín, guitarra... etc. Tienen cuerdas de distintos
grosores (distinta densidad lineal) y todas tienen idéntica longitud. Si proporcionamos a dos de
ellas idéntica tensión, la frecuencia del primer armónico será mayor (sonido más agudo) para la
más ligera:
Combinando tensión y densidad lineal es posible "afinar" las cuerdas del instrumento para que
cada una de ellas emita la frecuencia deseada.
Para un violoncello, si empezamos por la cuerda más gruesa y terminamos por la más fina, las
frecuencias son:
66 Hz (Do2), 99 Hz (Sol2), 148,5 Hz (Re3) y 220 Hz (La3)
(1)
4. Mantenemos fija la cuerda (µ), la tensión (T) y su longitud (L). Si pulsamos se pueden generar
varias frecuencias simultáneamente, correspondientes a n=1, n=2, n=3... etc.
Es decir, además del tono fundamental (o primer armónico) se generan otros armónicos con
frecuencias doble, triple... etc del fundamental. Los armónicos generados, y su amplitud,
dependen de varios factores tales como la constitución de las cuerdas, el material de que está
hecho el instrumento, su geometría... etc.
La combinación de armónicos permite distinguir entre un mismo sonido producido por
instrumentos diferentes, dándoles su timbre característico.
(1)
La4 tiene una frecuencia de 440 Hz. Es el sonido usado como referencia para la afinación de los
instrumentos. El La una octava más bajo tiene 220 Hz (La3), dos octava más bajo 110 Hz (La2) y tres octava
más bajo 55 Hz (La1). Con las demás notas se procede de forma análoga.
n T
f
2 L
=
µ
n T v
f n
2 L 2 L
= =
µ

4
Si tomamos una cuerda y, pulsándola (como se hace en los instrumentos de cuerda), acortamos
su longitud a la mitad, un cuarto... etc, la frecuencia del sonido fundamental aumenta al doble, al
cuádruple, etc., produciendo sonidos el doble y el cuádruple de agudos que el fundamental
(una octava, o dos, más altos que el fundamental).
Combinación de tres MAS
(resultante en negro) con las
siguientes características:
T1 = 4,0 s A1 = 1,00 m
T2 = 2,0 s A1 = 0,50 m
T3 = 1,0 s A1 = 0,25 m
Combinación de tres MAS
(resultante en negro) con las
siguientes características:
T1 = 4,0 s A1 = 1,00 m
T2 = 2,0 s A1 = 0,30 m
T3 = 1,0 s A1 = 0,15 m

1
Ondas sonoras
Sonido
IES La Magdalena.
Avilés. Asturias
Cuando algo vibra en el aire esta vibración se transmite al aire originando una onda sonora.
Una onda sonora es una onda de presión motivada por el desplazamiento de porciones de aire en el
sentido en el que se desplaza la onda (es, por tanto, una onda longitudinal). Este desplazamiento adelante y
atrás provoca zonas en las que el aire se acumula haciendo que la presión sea máxima (puntos negros) y
otras en las que se produce una presión negativa: zonas de depresión o enrarecimiento (espacio en
blanco).
Las ondas sonoras, por tanto, son ondas materiales, ya que necesitan el aire (u otro medio elástico) para su
propagación y, en consecuencia, no se pueden propagar en el vacío.
Una onda sonora transmite, por tanto, energía de un punto a otro haciendo que los puntos del medio oscilen
con una amplitud y frecuencia determinadas. Por tanto, todos los conceptos tratados en el estudio de las
ondas son aplicables aquí. Ahora bien, las ondas sonoras pueden ser percibidas por nuestro oído
produciéndonos sensaciones. Por eso a la hora de estudiar el sonido es importante diferenciar la parte
física del mismo de la sensación fisiológica que nos produce.
Las ondas de presión transmitidas por el aire golpean el tímpano, una membrana elástica situada al final
del canal auditivo, en el oído externo,. Las vibraciones del tímpano son transmitidas a tres huesecillos
situados en el oído medio: martillo, yunque y estribo. Este último está pegado a la cóclea o caracol (oído
interno) y le transmite las vibraciones
recibidas. En el interior de la cóclea
existen líquidos que transmiten las
vibraciones hasta las células ciliadas
que transforman las vibraciones en
impulsos eléctricos que se transmiten
a través del nervio auditivo al
cerebro, donde se "interpreta" la
información provocando en nosotros
la sensación sonora correspondiente.
Es esta sensación sonora lo que
llamamos "sonido". El término
"onda sonora" lo emplearemos para
referirnos a la perturbación que se
transmite a través del medio.
El oído humano sólo es capaz de
percibir sonidos comprendidos entre
los 20 y los 20 000 Hz, aunque su
sensibilidad no es la misma para las
diferentes frecuencias (de manera general para frecuencias bajas se requieren intensidades más elevadas
para percibir el sonido).
Con la edad las células sensibles a las frecuencias más altas se van deteriorando, por esa razón con la
edad se va perdiendo audición para las frecuencias superiores. Este daño también puede producirse por
una exposición prolongada a sonidos de elevada intensidad (escuchar música con auriculares y a un
volumen elevado)
Desplazamiento de la onda
Pistón (u objeto vibrante) que empuja
el aire adelante y atrás provocando
las variaciones de presión.
Enrarecimiento Compresión
λ
Ilustración: Wikipedia

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Ondas sonoras. Sonido
2
La velocidad a la que viaja una onda sonora (como cualquier onda)
depende de las características del medio en el cual se propaga. En
general, cuanto más rígido sea el medio más rápidamente se
propagarán las ondas. Así el sonido viaja con mayor velocidad en los
sólidos que en los líquidos, y en estos más rápido que en los gases
(ver tabla).
En los gases la velocidad es directamente proporcional a la raíz
cuadrada de la temperatura absoluta:
Donde k es una constante para cada gas.
Ejemplo 1
Si la velocidad del sonido en el aire es de 330 m/s a 0
0
C, calcular la velocidad con que se propaga a 20
0
C
Solución:
Se define la intensidad de una onda como la energía que atraviesa por segundo la unidad de superficie
colocada perpendicularmente a la dirección de propagación.
La intensidad puede definirse también como la potencia por unidad de
superficie (perpendicular a la dirección de propagación) y se mide en W/m
2
.
La intensidad de una onda de frecuencia dada es proporcional al cuadrado de
su amplitud (ver tema dedicado al movimiento ondulatorio).
Las intensidades que el oído humano es capaz de detectar abracan un
amplísimo rango, ya que van desde aproximadamente 10
-12
W/m
2
(1 pW/m
2
), que suele considerarse como
el nivel mínimo de audición (llamado umbral de audición), hasta 1 W/m
2
.
Las presiones correspondientes a estos niveles extremos son 3.10
-5
Pa y
29,2 Pa (la presión atmosférica "normal" es de 101 325 Pa).
Supongamos que una fuente (altavoz) emite una onda con una potencia P
que viaja en todas direcciones. Si suponemos una situación ideal en la que
no se pierde energía por absorción, la potencia inicial se irá repartiendo
entre los sucesivos frentes de onda (que suponemos esféricos en el
espacio tridimensional), de forma tal que las intensidades a distancias R1 y
R2 del centro emisor serán:
Medio v (m/s)
Aire 330 - 340
Agua 1 400 - 1 500
Tierra o arena 2 000 - 3 000
Rocas compactas 5 000 - 6 000
Hierro 4900
Velocidad de propagación de las ondas sonoras
v k T=
v k T ; v k T
kv
v
= =
=
1 1 2 2
1
2
T
k
1 T
TT
v T
v T
T m K
v v
T s
=
=
= =
1
22
1 1
2 2
2
2 1
1
293
330
K273
m
s
= 342
Intensidad de las ondas sonoras
E E
I ; Como : P
t S t
P
I
S
= =
=
P P
I ; I
S S
P I S I S
= =
= =
1 2
1 2
1 1 2 2

3
Dado que la superficie de una esfera vale:
Tenemos:
La intensidad disminuye proporcionalmente al cuadrado de la distancia al centro emisor, fenómeno
conocido con el nombre de atenuación de la intensidad.
La disminución de la intensidad con el cuadrado de la distancia puede explicarse de manera intuitiva ya que
la energía comunicada por la fuente a los puntos del medio debe distribuirse entre más puntos a medida
que la onda se aleja del centro emisor (la superficie del frente de onda aumenta según ) y, en
consecuencia, la potencia por unidad de superficie disminuye.
En la realidad la intensidad, además de disminuir debido al fenómeno de la atenuación, sufre también una
merma debido a la absorción por las partículas del medio, ya que parte de la energía que la onda
debería transmitirles se disipa como calor.
La sensación sonora que produce en nosotros un aumento en la intensidad de un sonido no se
corresponde con el incremento real, ya que para apreciar un aumento de intensidad doble se precisa que la
intensidad física sea diez veces mayor, por eso se establece una nueva magnitud denominada nivel de
intensidad sonora o sonoridad de un sonido:
Donde I es la intensidad del sonido considerado e I0= 10
-12
W/m
2
un nivel de referencia (arbitrario) y que se
corresponde, de modo aproximado, con el sonido más débil que puede ser percibido.
El nivel de intensidad de un sonido es una magnitud adimensional. La unidad en que se mide recibe el
nombre de decibelio (dB) en honor de Alexander Graham Bell (1847-1922)
En esta escala el umbral de audición (10
-12
W/m
2
) se corresponde con:
y el límite superior (llamado umbral de dolor) con:
En la tabla se dan algunos valores típicos de niveles de intensidad de algunos sonidos comunes.
Sonido dB Comentario
0 Umbral de audición
Respiración normal 10 - 20
Conversación en voz baja 20 - 40
Sonidos bajos
Conversación normal 40 - 60
Ruidos corrientes. Se pueden soportar
permanentemente
Calles ruidosas. Fábrica mediana. 60 - 80 Soportables, pero pueden producir fatiga
Gritos humanos, silbato agudo 80 - 90
Martillo neumático (exterior). Metro 90 - 100
Ruidos molestos
Martillo neumático a 1 m
Despegue avión (a 60 m)
100 -120 Sólo soportables durante un tiempo
I
log
I
β =
0
10
I W /m
log log dB
I W /m
−
−
β = = =
12 2
12 2
0
10
10 10 0
10
I W /m
log log dB
I W /m−
β = = =
2
12 2
0
1
10 10 120
10
S R= π 2
4
I S I S ; I R I R
I R
I R I R ;
I R
= π = π
= =
2 2
1 1 2 2 1 1 2 2
2
2 2 1 2
1 1 2 2 2
2 1
4 4
S R= π 2
4
Como la intensidad es proporcional al cuadrado de
la amplitud, también podemos escribir:
I A A R A R
; ;
I AA A R R
= = =
2 2 2
1 1 1 2 1 2
2 2 2
2 22 2 1 1

4
La gráfica de la derecha representa el
área de audición (ideal) y en ella se
muestran niveles de intensidad (dB)
frente a frecuencias (Hz).
Se puede observar en la gráfica que
la sensibilidad del oído humano es
máxima para frecuencias entre 2 000
y 3 000 Hz.
La línea roja señala el límite superior
o umbral de dolor. Este umbral es
aproximadamente constante y se
sitúa en torno a los 120 dB.
Los sonidos audibles se localizan en
el área limitada por ambas curvas.
Sólo un 1% de las personas tiene
unos niveles de audición similares a
los que se muestran en la gráfica.
Realmente el 90 % de las personas
sólo perciben un sonido de 2 500 Hz
cuando el nivel de intensidad es de unos 20 dB.
Los sonidos de frecuencias bajas necesitan de intensidades relativamente altas para ser percibidos. Los
sonidos fuertes (de unos 80-100 dB) pueden ser percibidos en todo el espectro de frecuencias.
Las cualidades generalmente asociadas al sonido son:
• Intensidad
• Tono
• Timbre
En algunas ocasiones se considera también la duración del sonido como una cualidad de éste.
La intensidad del sonido está relacionada (como ya se ha visto) con su amplitud. Es la cualidad que
permite clasificar un sonido como "fuerte" o "débil".
El tono está relacionado con la frecuencia y es la cualidad que nos permite clasificar los sonidos en agudos
(frecuencias altas) o graves (frecuencias bajas). Como se ha visto el oído humano sólo es capaz de apreciar
Cualidades del sonido
Sonidos de idéntica frecuencia (100 Hz) y con distinta
intensidad. El representado por la línea azul tiene
doble intensidad que el representado por la línea roja

5
sonidos con frecuencias comprendidas entre 20 y 20 000 Hz. Por debajo del límite inferior están los
llamados infrasonidos y por encima los ultrasonidos.
Algunos animales como delfines y murciélagos son capaces de oír sonidos de hasta 200 000 Hz.
El timbre está relacionado con la cantidad de armónicos que "acompañen" a las notas fundamentales y su
amplitud relativa, ya que cualquier instrumento musical (incluidas nuestras cuerdas vocales) nunca emiten
sonidos puros (las notas puras sólo son emitidas por diapasones), sino una mezcla de la nota fundamental y
varios de sus armónicos.
Dependiendo de los materiales de que está hecho, de sus medidas, etc, cada instrumento emite un sonido
característico con su timbre particular.
El timbre nos permite distinguir claramente entre un La (por ejemplo) emitido por un violonchelo, un clarinete
o una trompeta. Asimismo el timbre nos permite distinguir a dos personas que emiten el mismo sonido.
Para comprobar la influencia de los armónicos en el sonido escuchado ver:
http://www.falstad.com/loadedstring/
Notas f (Hz)
Do 264
Re 297
Mi 330
Fa 354
Sol 396
La 440
Si 495
Sonidos de diferente frecuencia: 50 Hz (línea roja) y
100 Hz (línea azul). Buscando una mayor claridad de la
gráfica se han dado también diferentes amplitudes.
Sonido (onda con línea continua) producida por la combinación de los tres primeros armónicos
(líneas de puntos) con amplitudes relativas distintas.
En la figura de la izquierda las amplitudes relativas son A1 , A2 = A1/2 y A3 = A1/ 4
En la de la derecha A1 , A2 = 3/4 A1 y A3 = 3/4 A1

6
Ejemplo 2
En la figura se muestra la gráfica de
un sonido (v = 340 m/s).
a) Calcular su longitud de onda y su
frecuencia.
b) Suponer que el nivel de intensidad
sonora a cierta distancia del foco
es de 60 dB. ¿Cuál será su
intensidad en W/m
2
?
c) ¿Cuál es la relación entre las
intensidades de dos sonidos cuyo
nivel de intensidad difiera en 20
dB?
d) ¿Cuál será la intensidad de la
onda si se mide a una distancia
doble?
Dato: I0 = 10
-12
W/m2
Solución:
a) En la figura se puede observar que una distancia de 5, 0 m comprende 5/2 longitudes de onda (2 +1/2).
Por tanto:
Para calcular la frecuencia:
b) Recordando la definición de la escala de nivel de intensidad sonora (dB) y operando:
c)
d) Como la intensidad de una onda decrece proporcionalmente al cuadrado de la distancia:
, m
, m
λ =
λ =
5
5 0
2
2 0
m
v
f v ; fλ = = =
λ
340
s
, m2 0
s (Hz)−
= 1
170
I I
log ; log
I I
I W W
; I I
I m m
β β
− −
β
β = =
= = = =
0 0
60
12 610 10 10
0 2 2
0
10
10
10 10 10 10 10
( )
I R R R I W /m W
; I I I ,
I R R mR
−
−
= = = = = =
2 2 2 6 2
71 2 1 1 1
2 1 12 2 2 2
2 1 2 1
10
2 5 10
4 42
I I
log ; log
I I
I
II I
log log log
I I
β = β =
 
β − β = ∆β = − = 
 
1 2
1 2
0 0
2
02 1
2 1
0 0
10 10
10 10
I
I
1
0
I
log
I
I I I
log ; log ; ; I I
I I I
I I I
∆β ∆β
=
∆β
∆β = = = =
= =
2
1
2 2 2 10 10
2 1
1 1 1
20
210
2 1 1
10
10 10 10
10
10 10

1
Determinación de la velocidad
del sonido en el aire
IES La Magdalena.
Avilés. Asturias
(Información complementaria en FisQuiWeb: http://bit.ly/1xng29O)
El sonido es una onda de presión que viaja en el aire con una velocidad aproximada de 330- 340 m/s.
Si se produce un sonido en el interior de un tubo se generará una onda estacionaria si
se cumplen las llamadas condiciones de contorno para los extremos: que exista un
nodo en el extremo del tubo, si está cerrado, o un vientre, si está abierto.
Esta circunstancia permite diseñar un experimento en el cual se utilizan las ondas
sonoras estacionarias que se pueden formar en un tubo para determinar la velocidad
de propagación del sonido en el aire.
El montaje experimental utilizado para la obtención de los datos es el que se muestra
en el esquema de la derecha.
El tubo es de plástico transparente, de unos 65 cm de longitud, y se tapa por la parte
inferior con un corcho al que se adapta una llave de paso para líquidos. También se
pega con cinta adhesiva una cinta métrica para poder hacer las mediciones. En la
parte superior se fija un diapasón de 440 Hz.
Cuando se golpea el diapasón la onda sonora penetra en el tubo y se refleja en la
superficie del líquido que lo llena parcialmente. Como consecuencia se puede formar
en su interior una onda estacionaria si se da una doble condición: que exista un nodo
en la superficie del líquido y un antinodo, o vientre, en la parte abierta del tubo. Esto
sucederá cuando la longitud del tubo, no ocupada por el agua, sea un múltiplo impar
de un cuarto de la longitud de onda.
Cuando se cumpla esta condición se formará la onda estacionaria, que se detecta porque se produce un
súbito aumento de la intensidad del sonido. La longitud del tubo se puede variar abriendo la llave y de-
jando que el agua vierta en el vaso.
Se determina (varias veces) la longitud a la cual se aprecian variaciones en la intensidad del sonido.
La relación existente entre velocidad, frecuencia y longitud de onda es:
Sustituyendo el valor de la longitud de onda obtenemos la ecuación que nos da la velocidad del sonido
en función de la frecuencia de la onda y la longitud del tubo:
v f= λ
L n n 1,3, 5, 7...
4
4L
n 1,3,5,7...
n
λ
= =
λ = =
4f
v f L
n
4f
v L n 1, 3, 5, 7...
n
 
= λ =  
 
 
= = 
 

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Velocidad del sonido en el aire
2
En la experiencia se han tomado datos para los dos primeros armónicos (ver figura). Los datos obtenidos se
recogen en las tablas adjuntas:
n = 1
L (cm)
1 19,0
2 19,5
3 18,7
4 19,3
5 18,5
n = 3
L (cm)
1 57,7
2 57,2
3 58,0
4 57,5
5 58,2
Consideramos, por tanto, como valor verdadero: 336 m/s.
Calculamos el error absoluto de la medida que más se desvía del valor verdadero (326 m/s)
El error relativo (que nos da la calidad de la medida) será:
La medida la expresaremos con la incertidumbre en la forma (ver cálculo de errores en FisQuiWeb):
Otra posibilidad consiste en calcular la incertidumbre de la media según:
Para este caso:
Calculamos para cada uno de los valores la velocidad del sonido
(con tres cifras significativas).
A continuación se realiza un cálculo de ejemplo para n = 1 y n = 3.
Los valores obtenidos se recogen en la tabla adjunta.
v (m/s)
1 334
2 343
3 329
4 340
n=1
5 326
6 337
7 336
8 340
9 337
n=3
10 341
Media 336
1
1
4L 4 . 0,190 m m
v f 440 s 334
n 1 s
4L 4 . 0,577 m m
v f 440 s 339
n 3 s
−
−
 
= = = 
 
 
= = = 
 
( )a med verd
m m
E V V 326 336 10
s s
= − = − = −
a
r
verd
m
10
E s
E .100
V
= =
m
336
s
.100 3 %=
( )
m
v 340 10
s
= ±
2
i
m i
(x x)
x medida i;x media ; n número de datos
n (n 1)
Σ −
σ = = = =
−
( )m
m m m
1,7 2 Luego : v 336 2
s s s
σ = = = ±

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Movimiento Armónico Simple (MAS)
Un ejemplo de MAS es el de la proyección sobre el diámetro de la circunferencia de la posición de un punto que gira con velocidad angular constante:
Se dice que una partícula oscila cuando tiene un movimiento de vaivén respecto de su
posición de equilibrio, de forma tal que el movimiento se repite en cada oscilación. De todos
los movimientos oscilatorios el más sencillo, y el más importante, es el movimiento
armónico simple (MAS). Muchos fenómenos naturales pueden considerarse armónicos
simples y, además, cualquier movimiento oscilatorio más complejo se puede resolver como
una suma de varios MAS (aplicando un método matemático llamado método de Fourier).
0= = ω ω + ϕ
dx
v A cos( t )
dt
2
2
02
= = = − ω ω + ϕ
d x dv
a A sen( t )
dtdt
2 2
= ω −v A x 2
= − ωa x
x A sen ( t )
x
x A sen ( ); sen ( )
A
= ω + ϕ
= ϕ ϕ =
0
0
0 0 0
x =Ax = - A
a= 0 v max
v max a= 0
a max v= 0a maxv= 0 va
v a
va
v a
0
3
2
π
ϕ =
0ϕ = π
0
2
π
ϕ =0 0ϕ =
F m a A m sen ( t) A k sen ( t)= = − ω ω = − ω2
2
= = − ω = −F m a m x k x
k m m m
T T
m
T m
k k
k
f
T mm
k
π π 
= ω = = 
 
π
= = π
= = =
π
π
2 2
2
2
2
2 4
4
2
1 1 1
2
2
Un cuerpo de masa m oscilará con MAS si está sometido
a una fuerza que varía con el tiempo en la forma:
2= π
L
T
g
La fuerza elástica es una fuerza conservativa ya que cuando realiza
trabajo negativo resta energía cinética al cuerpo que se transforma en
energía potencial elástica. La energía potencial acumulada puede volver
a convertirse en energía cinética dejando que la fuerza elástica actúe
(realizando trabajo positivo)
2
p
1
E k x
2
= 2 2 21 1
2 2
+ = ω =Ec Ep m A k A
Los movimientos oscilatorios
reales por ejemplo la oscilación
de un péndulo) van perdiendo
amplitud hasta que, lentamente,
se detienen debido a la acción
de fuerzas no conservativas
(rozamientos) que convierten la
energía cinética en calor. Se
dice que las oscilaciones se
amortiguan, lo que se traduce
en una disminución progresiva
de la amplitud hasta la extinción
total de las oscilaciones.
La forma más efectiva de comunicar energía a un oscilador es
cuando la frecuencia de la fuerza externa coincide (aunque sea de
forma aproximada) con la frecuencia natural del oscilador, Cuando se
suministra energía a un sistema oscilante con una frecuencia igual a su
frecuencia de oscilación natural se dice que se produce resonancia, la
energía del oscilador aumenta entonces en cada aportación pudiendo
adquirir valores muy altos.
En un MAS la fuerza es proporcional
al desplazamiento y opuesta a él
Para pequeñas oscilaciones (ángulo
inferior a 20
0
) un péndulo simple se
comporta como un oscilador
armónico de constante k = mg/L

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Fenómenos ondulatorios. Sonido
Cuando la perturbación que constituye la
onda alcanza los puntos del medio, éstos
se convierten en fuentes secundarias de
ondas y se puede obtener el nuevo frente
de ondas trazando la envolvente de las
ondas secundarias emitidas (Principio de
Huygens). El proceso se puede repetir, con
lo que podemos seguir la propagación de la
onda a través del medio.
La difracción tiene lugar cuando las ondas que se
propagan encuentran un obstáculo cuyas dimensiones
son del orden de la longitud de onda de las ondas
incidentes. Las ondas se propagan entonces como si
el orificio se convirtiera en un nuevo centro emisor
(Huygens) y penetran tras el orificio en lo que debería
de ser una "zona de sombra" si su comportamiento
fuera como el de un chorro de partículas.
La interferencia entre dos ondas tiene
lugar cuando ambas coinciden en una
región del espacio al mismo tiempo.
Cuando esto sucede ambas se suman
(principio de superposición) produciendo
una onda resultante.
La interferencia se produce únicamente
en los puntos en que ambas ondas
coinciden. Si, por ejemplo, ambas se
desplazan en sentidos contrarios
interferirán cuando se encuentren y
después ambas ondas siguen su camino
sin sufrir alteración.
Si la fase es idéntica se produce lo que se llama
interferencia constructiva. Las amplitudes de
ambas ondas se suman : A = A1 + A2.. Esto sucede
cuando la diferencia entre las fases sea:
n (n , , ...)∆ϕ = π =2 0 1 2
Si las ondas están en oposición se produce lo que se llama
interferencia destructiva Las amplitudes de ambas ondas
se restan : A = A1 - A2. Si A1 = A2 la onda resultante tiene una
amplitud nula (se produce la extinción). Esto sucede
cuando la diferencia en fase sea:
( )n (n , , ...)∆ϕ = + π =2 1 0 1 2
Arriba onda transversal NO
polarizada.
Abajo onda transversal
polarizada. La oscilación se
produce sólo en el plano
vertical.
La polarización es una propiedad especialmente
importante en el caso de ondas electromagnéticas..
En una onda electromagnética polarizada el plano de
oscilación del campo eléctrico es siempre el mismo.
El llamado efecto Doppler consiste en el cambio
de frecuencia percibido por un observador
cuando se mueve respecto de la fuente que emite
las ondas.
El efecto Doppler permitió a Edwin Hubble en 1929
afirmar que las galaxias no estaban quietas y la
mayoría se movían alejándose de nosotros con una
velocidad directamente proporcional a la distancia
que nos separa de ellas

Física 2º Bachillerato. IES La Magdalena. Avilés. Asturias Fenómenos ondulatorios. Sonido
Cuando algo vibra en el aire esta vibración se transmite originando una onda sonora
Una onda sonora es una onda de presión motivada por el desplazamiento de porciones de aire
en el sentido en el que se desplaza la onda (es, por tanto, una onda longitudinal).
Desplazamiento de la onda
Pistón (u objeto vibrante) que empuja
el aire adelante y atrás provocando
las variaciones de presión.
Enrarecimiento Compresión
λ
La velocidad a la que viaja una onda sonora depende de las características
del medio en el cual se propaga. En general, cuanto más rígido sea el medio
más rápidamente se propagarán las ondas sonoras. Así el sonido viaja con
mayor velocidad en los sólidos que en los líquidos, y en estos más rápido que
en los gases .
En los gases la velocidad es directamente proporcional a la raíz cuadrada de
la temperatura absoluta:
=v k T
Se define la intensidad de una onda como la energía que atraviesa por segundo la unidad de
superficie colocada perpendicularmente a la dirección de propagación.
La intensidad puede definirse también como la potencia por unidad de superficie
(perpendicular a la dirección de propagación). Se mide en W/m
2
2
1 2
2
2 1
=
I R
I R
I A A R A R
; ;
I AA A R R
= = =
2 2 2
1 1 1 2 1 2
2 2 2
2 22 2 1 1
La sensación sonora que produce en nosotros un
aumento en la intensidad de un sonido no se corresponde
con el incremento real, ya que para apreciar un aumento
de intensidad doble se precisa que la intensidad física sea
diez veces mayor, por eso se establece una nueva
magnitud denominada nivel de intensidad sonora o
sonoridad de un sonido.
El nivel de intensidad de un sonido es una magnitud
adimensional. La unidad en que se mide recibe el nombre
de decibelio (dB)
I
log
I
β =
0
10 I0= 10
-12
W/m
2Sonidos de idéntica frecuencia
y con distinta intensidad.
Sonidos de diferente
frecuencia
Sonido (onda con línea continua)
producido por la combinación de los tres
primeros armónicos (líneas de puntos)
con amplitudes relativas distintas.
La intensidad del sonido está
relacionada con la amplitud.
El tono está relacionado
con la frecuencia
El timbre está relacionado con
la cantidad de armónicos y
su amplitud relativa.
Cualidades del sonido

Vibraciones y Ondas

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a Vibraciones y Ondas

Similar a Vibraciones y Ondas (20)

Último

Último (20)

Vibraciones y Ondas