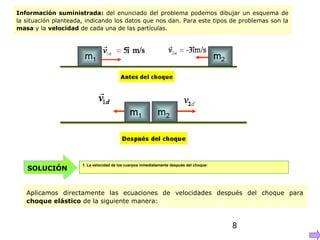
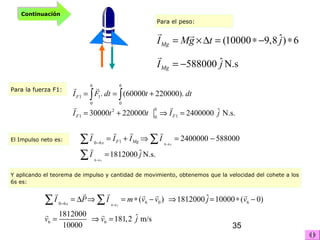
Este documento describe los conceptos de choque elástico e inelástico. En un choque elástico, la energía cinética total y la cantidad de movimiento se conservan. Las ecuaciones para calcular las velocidades después del choque se presentan. En un choque inelástico, solo se conserva la energía asociada al centro de masa, por lo que hay pérdida de energía cinética total.