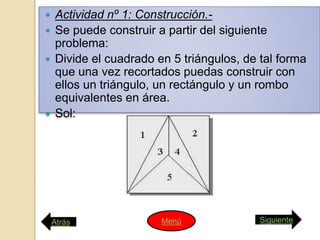
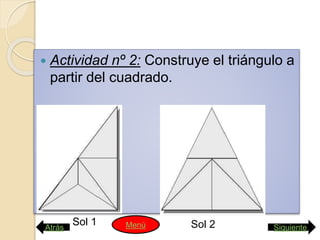
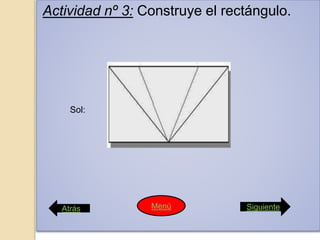
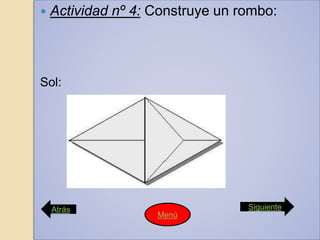
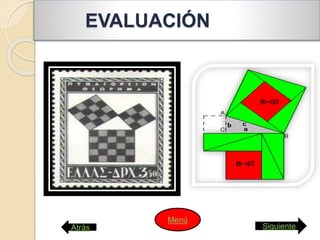
Este documento presenta las instrucciones para una actividad escolar en la que dos estudiantes prepararán una conferencia sobre el Teorema de Pitágoras y sobre la vida y obra de Pitágoras para presentar a sus compañeros. La conferencia constará de cinco partes: 1) una demostración visual del teorema usando un rompecabezas, 2) comprobar que solo se aplica a triángulos rectángulos, 3) otra demostración visual, 4) ejemplos de problemas resueltos con el teorema, y 5) una entrevista

1. TEOREMA DE PITÁGOTA
INTRODUCCIÓN
TAREA
PROCESO
RECURSOS
EVALUACIÓN
CONCLUCIÓN

2. INTRODUCCIÓN






 ¡Dí el nombre de un matemático famoso!
Seguro que has pensado en el mismo que la mayoría, pero ¿qué sabes de la
vida de Pitágoras? ¿En qué época y lugar vivió? ¿Cómo era y qué ideas tenía?
Intentaremos averiguarlo y además visualizaremos y entenderemos mejor el
teorema que lo ha hecho tan famoso. Al final van a darle una charla a sus
compañeros para contarles lo más interesante y significativo de lo que aprendáis.
Este trabajo fue hecho con el propósito de saber y aprender como se resuelven
los problemas y como se aplica en cada determinado tipo de problemas y como
resolverlos.
Atrás siguiente
Menú

3. TAREA


El propósito final de la actividad es que
nuestro grupo de dos estudiantes prepare
y desarrolle una conferencia ante los
compañeros de clase (o de otra clase)
sobre el Teorema de Pitágoras y sobre el
mismo Pitágoras.
atrás SiguienteMenú

4.  Actividad nº 1: Construcción.-
 Se puede construir a partir del siguiente
problema:
 Divide el cuadrado en 5 triángulos, de tal forma
que una vez recortados puedas construir con
ellos un triángulo, un rectángulo y un rombo
equivalentes en área.
 Sol:
Atrás SiguienteMenú

5.  Actividad nº 2: Construye el triángulo a
partir del cuadrado.
Sol 1 Sol 2Atrás SiguienteMenú

6. Actividad nº 3: Construye el rectángulo.
Sol:
Atrás SiguienteMenú

7.  Actividad nº 4: Construye un rombo:
Sol:
Atrás Siguiente
Menú

8. PROCESO
 La conferencia constará de cinco partes y cada uno de los miembros del
grupo será el encargado de exponer una de esas partes (salvo la quinta
que será responsabilidad de dos compañeros)
 1ª Parte: Se trata de utilizar un puzzle de cartulina para explicar el
significado geométrico y comprobar la validez del Teorema de Pitágoras.
encontraran las instrucciones para la construcción de dicho puzzle (En el
apartado "una sencilla comprobación").
 2ª Parte: Comprobar, valiéndose de la figura que encuentren o del
geoplano de (y del video proyector), cómo el Teorema de Pitágoras se
cumple sólo para triángulos rectángulos.
Se trata de construir triángulos sobre el Geoplano y luego cuadrados sobre
cada lado, comprobando las correspondientes áreas.
 3ª Parte: También con el video proyector, podrán explicar una
demostración visual del teorema. Tendrán que elegir la que más les guste
entre las que encuentren.
 4ª Parte: Tendrán que aclarar la utilidad práctica del teorema,
ejemplificándolo con dos o tres problemas en cuya resolución se
aproveche el teorema.
y encontrar múltiples ejemplos de problemas.
 5ª Parte: Se trata de emitir una entrevista radiofónica grabada previamente
a Pitágoras, o si lo prefieren, escenificar la entrevista en clase. Uno de los
miembros del grupo asumirá el papel de periodista y otro el de el propio
Pitágoras.Atrás SiguienteMenú

9. RECURSOS
 WEBLIOGRAFÍA:
 http://docentes.educación.navarra.es
 http://html.rincondelvago.com
Atrás SiguienteMenú

10. EVALUACIÓN
Atrás Siguiente
Menú

11. Cada miembro del grupo recibirá dos notas: una específica por la parte de la que es responsable
y otra global (la misma para todos) por la evaluación de toda la sesión.
 Aspectos a valorar positivamente:
En todas las tareas:
 Expresarse con orden y coherencia.
 Dejar claros los aspectos fundamentales.
 Expresarse de forma apropiada y con naturalidad.
 Gestionar los tiempos dedicados a cada parte de manera equilibrada.
 Conectar las diferentes partes de la exposición de modo que haya coherencia en el conjunto y no
se perciban como exposiciones independientes y sin relación.
 Dar pie a la participación de los compañeros y la aclaración de sus dudas.
 En la 1ª Parte (el Puzzle):
 Transmitir con claridad tanto el proceso de construcción como su utilidad para comprobar el
Teorema
 En la 2ª Parte (el Geoplano interactivo):
 Acertar con ejemplos claros de triángulos.
Atrás SiguienteMenú

12.  Utilizar algún triángulo de base oblicua.
 Dejar claras las propiedades que se cumplen para cada tipo de triángulos (acutángulos, rectángulos y
obtusángulos).
 En la 3ª Parte (Demostración interactiva):
 Explotar las posibilidades de la figura.
 No limitarse a un único triángulo
 En la 4ª Parte (los Problemas):
 Que no sean problemas exclusivamente de Matemáticas: que planteen una situación de la vida real.
 Que los problemas seleccionados tengan un contexto lo más cercano y atractivo posible para los
compañeros.
 Que alguno de los problemas tenga un ámbito en el espacio (no limitarse a problemas sobre el plano).
 Suscitar el interés de los compañeros e invitarles a que sugieran posibles caminos para la solución (mejor si
éstos no son evidentes)
 En la 5ª Parte (el Entrevistador o Periodista):
 Conseguir un estilo periodístico que suscite el interés en el público.
 Cuestionar que el Teorema se llame de Pitágoras.
 Preguntar por los aspectos fundamentales en la vida y obra de Pitágoras.
 Preguntar por los pitagóricos.
 Tratar al personaje con el respeto que merece.
 Dar pie a alguna pregunta de los compañeros.
 En la 5ª Parte (el Entrevistado o Pitágoras):
 Dar una visión clara de las aportaciones de Pitágoras a la cultura (matemática, filosófica y astronómica) de la
época.
 Reconocer y argumentar cómo el teorema era conocida antes de la época de Pitágoras.Atrás SiguienteMenú

13. CONCLUSIÓN
 Este trabajo se trato sobre el teorema
de Pitágoras cómo se debe de
resolver, cuáles son sus aspectos y
cómo aplicarlo en cada determinado
tipo de temas.
Atrás Menú