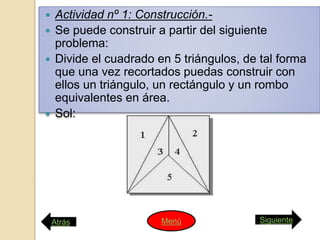
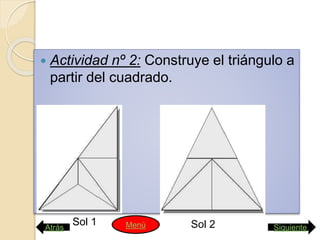
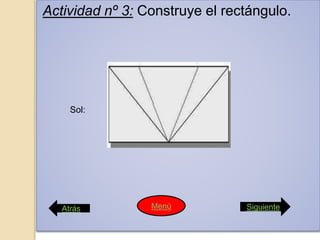
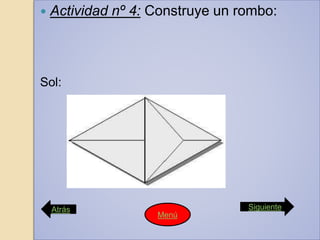
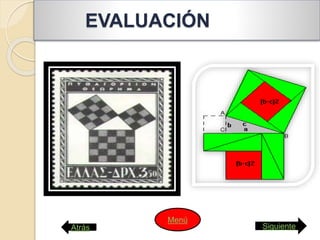
Este documento presenta las instrucciones para una actividad escolar sobre el Teorema de Pitágoras. Los estudiantes prepararán una conferencia en 5 partes para sus compañeros: 1) Usarán un rompecabezas para demostrar visualmente el teorema, 2) Comprobarán el teorema en triángulos rectángulos usando un geoplano, 3) Explicarán demostraciones visuales, 4) Presentarán problemas resueltos con el teorema, 5) Entrevistarán a Pitágoras sobre su vida y obra. El documento