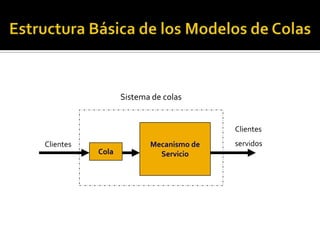
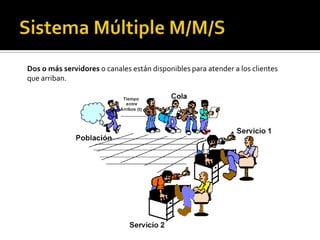
La teoría de colas se refiere al estudio matemático de las líneas de espera, permitiendo analizar procesos como llegadas y espera. Sus objetivos son predecir resultados del sistema, evaluar estrategias y dimensionar el sistema controlando la entrada y el grado de servicio. Los modelos básicos incluyen una fuente de entrada, cola y mecanismo de servicio. La distribución de Poisson se usa comúnmente para modelar las llegadas mientras que los tiempos de servicio siguen una distribución exponencial.

1. Simulación de Sistemas Introducción a la Teoría de Colas Karina Alexandra Ojeda Herrera

2. Teoría de Colas…Se refiere al estudio matemático de las líneas de espera, permitiendo así el análisis de varios procesos como: llegada, espera en la cola etc.

3. Objetivos de la Teoría de ColasPredecir los resultados del sistema.Evaluar estrategias alternativas para elegir la mejor.Determinar cómo Dimensionar el sistema

4. Controlar la entrada

5. Grado de servicio

6. RetardoEstructura Básica de los Modelos de ColasSistema de colasMecanismo deServicioClientesservidosClientesCola

7. Fuente de EntradaTamaño de población: Es el número total de clientes que pueden requerir servicio en determinado momento.Forma de las llegadas: Patrón estadístico mediante el cuál se generan los clientes a través del tiempo. ENTRADA

8. Distribución de PoissonP(x) = Probabilidad de x arribosX = Número de arribos por unidad de tiempo = Rata promedio de arriboE = 2.71828

9. ColaTamaño de la cola: Una cola puede ser finita o infinita . El estándar es infinita.Disciplina de la cola: Se refiere al orden en el que se seleccionan sus miembros para recibir el servicio ( FIFO, Aleatoria, por prioridad ).

10. Mecanismo de servicioCanal: Hace referencia al número de servidores que hay en el sistema (Serie, Paralelo).Tiempo de Servicio: Es el tiempo que transcurre desde el inicio del servicio para un cliente hasta su terminación. La distribución más usada para los tiempos de servicio es la EXPONENCIAL.

11. NOTACION DE KENDALLLas distribuciones que utilizaremos son:• M: Distribución exponencial (markoviana)• D : Distribución degenerada (tiempos constantes)• Ek: Distribución Erlang• G : Distribución generalM / M / sModelo donde tanto los tiempos entre llegada como los tiempo de servicio son exponenciales y se tienen s servidores.M / M / 1Tiempos entre llegada exponenciales, tiempos de servicio general y 1 sólo servidor

12. Parámetros de un Proceso de Colas = frecuencia media de llegadasట= frecuencia media de servicioS=numero de servidoresPara que el sistema pueda alcanzar el régimen permanente es necesario que <= ట

13. Sistema Múltiple M/M/1

14. Sistema Múltiple M/M/SDos o más servidores o canales están disponibles para atender a los clientes que arriban.

15. Sistema Múltiple M/M/1/KUn solo servidor, capacidad de cola ilimitada y población infinita de arribos potenciales. Los tiempos entre arribos y los tiempos de servicio son distribuidos exponencialmente.