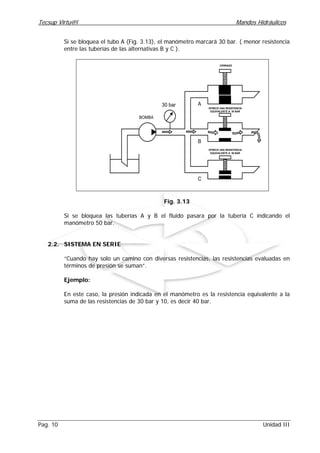
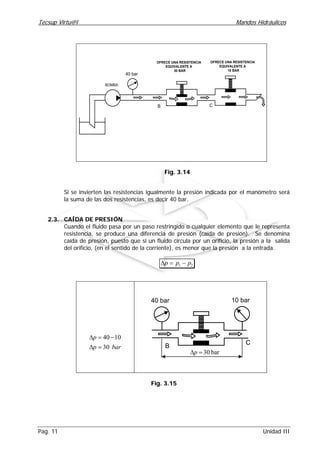
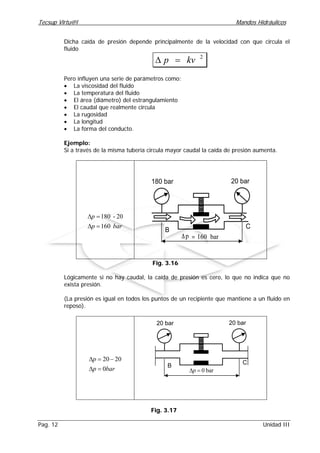
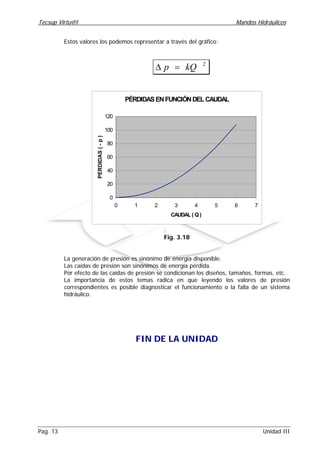
Este documento trata sobre caudal y generación de presión en sistemas hidráulicos. Explica conceptos clave como caudal, continuidad, desplazamiento volumétrico y medición del caudal. También describe cómo se genera presión cuando el caudal encuentra resistencia al fluir, ya sea a través de sistemas en paralelo o en serie. Finalmente, detalla cómo la presión en un sistema es la suma de las resistencias individuales cuando los caminos están conectados en serie.

1. UNIDAD III
Caudal y Generación de
Presión

2. Tecsup Virtu@l Indice
Índice
Unidad III : “Caudal y Generación de Presión”
1. CAUDAL ................................................................................................................... 1
1.1. FLUJO VOLUMÉTRICO ...................................................................................... 1
1.2. CONTINUIDAD ................................................................................................. 1
1.3. CAUDAL EN UNA BOMBA O MOTOR EN REGIMEN CONTINUO.
DESPLAZAMIENTO VOLUMÉTRICO .................................................................... 4
1.4. MEDICIÓN DEL CAUDAL ................................................................................... 5
1.4.1. CAUDALÍMETRO .................................................................................... 6
2. GENERACIÓN DE LA PRESIÓN ................................................................................... 7
2.1. SISTEMA EN PARALELO .................................................................................... 9
2.2. SISTEMA EN SERIE..........................................................................................10
2.3. CAÍDA DE PRESIÓN.........................................................................................11

3. Tecsup Virtu@l Mandos Hidráulicos
Pag. 1 Unidad III
UNIDAD III
“CAUDAL Y GENERACIÓN DE PRESIÓN”
1. CAUDAL
1.1. FLUJO VOLUMÉTRICO
El caudal es el flujo volumétrico. Es decir es el volumen de fluido V que fluye por un
punto en el tiempo t.
Q
V
t
=
V
12
6
39
t
Fig. 3.1
Ejemplo:
Si queremos llenar un depósito cuyo volumen es de 20 litros en el tiempo de dos
minutos, se necesita un caudal:
Q
V
t
l
min
l
min
= = =
20
2
10
Aplicación:
Con este concepto es posible determinar el caudal que entrega una bomba con solo
contar con un recipiente graduado y un reloj o cronómetro. Como aplicación practica
podríamos determinar el caudal (
l
min
) que entrega el caño de su casa, con la ayuda
de un balde con volumen conocido (comúnmente de 10 a 30 litros) y un reloj.
1.2. CONTINUIDAD
Por continuidad, para fluidos incompresibles, el caudal es el producto de la Velocidad
por el Area.
Q v A= ×
Q Q1 2=
v A v A1 1 2 2× = ×

4. Tecsup Virtu@l Mandos Hidráulicos
Pag. 2 Unidad III
Es muy común usar una relación alternativa que toma en cuenta la conversión de
unidades.
Q v A= × ×6 Donde:
Q
l
m i n
v
m
s
A c m
⇒
⇒
⇒ 2
Aplicación:
M
BOMBA HIDRAULICA
Q
D1
D0
QSUCCION
= Q
QDESCARGA
= Q
QEMBOLO
= Q QVASTAGO
Q≠
Fig. 3.2
La bomba envía caudal constante hacia el sistema en forma continua.
La bomba toma aceite del tanque y lo envía hacia el sistema.
La línea de succión tiene un mayor diámetro que la línea de descarga:
Luego concluimos:
• “El caudal es el mismo en la línea de succión y en la línea de descarga”.
• “La velocidad en la zona de succión es menor que en la zona de descarga ”.
• “El caudal en la tubería es igual al caudal en la zona del embolo del pistón”.
• “La velocidad del fluido es mayor en la tubería que en la zona del embolo del
pistón”.
• “El caudal en el lado del émbolo es diferente al caudal al lado del vástago del
cilindro”.
• “La velocidad es la misma al lado del émbolo que al lado del vástago”.

5. Tecsup Virtu@l Mandos Hidráulicos
Pag. 3 Unidad III
OBSERVACIONES:
• El teorema de continuidad se aplica a una línea de corriente por lo que el caudal
en el lado del embolo del cilindro es diferente al caudal en el lado del vástago POR
QUE NO HAY CONTINUIDAD:
QÉMBOLO ≠ QVÁSTAGO
• El desplazamiento del volumen de aceite determina la velocidad del actuador.
Luego: “Si un actuador pistón o motor está lento es porque no le llega suficiente
caudal y no porque le falte presión“.
• La RAPIDEZ CON QUE SE TRANSMITE LA SEÑAL ES DE:
s
m
v SEÑALNTRANSMISIO
600=−
• Como se observa los caudales y las áreas determinan la velocidad del fluido. Estas
velocidades del fluido están limitadas por las perdidas de energía que causan
debido al rozamiento entre el fluido mismo y el rozamiento con las tuberías por lo
que se recomienda las siguientes velocidades máximas en las tuberías de Sistemas
Hidraulicos:
VELOCIDAD
Líneas de Succión v < 1,5 m/s
Líneas de Retorno a Tanque v < 3,0 m/s
Líneas de Presión v < 5,0 m/s
Velocidad de los Actuadores v < 1,0 m/s
Ejemplo 1:
Determinar el caudal Q en l/min i en GPM que llega al pistón si tiene una velocidad de
salida de 0,1 m/s
M Q
Q LLEGA AL PISTON
QSALEDELPISTON
100 50
unidades: mm
v = 0,1 m / s
Fig. 3.3

6. Tecsup Virtu@l Mandos Hidráulicos
Pag. 4 Unidad III
Solución:
v
m
s
= 0 1,
A
D
cm= = =π π
2 2
2
4
10
4
78 54,
Q v A= × ×6
Q
m
s
cm
l
min
= × × =6 0 1 78 54 47 132
, , ,
45,12
785,3
1
13,47 =












=
min
l
GPM
x
min
l
Q
Ejemplo 2:
Determinar el caudal Q ( l/min ) que sale del pistón para el ejemplo anterior.
Solución:
v
m
s
= 0 1,
A
D d
cm=
−




 =
−




 =π π
2 2 2 2
2
4
10 5
4
58 90,
Q v A= × ×6
Q
m
s
cm
l
min
= × × =6 0 1 58 90 35 342
, , ,
1.3. CAUDAL EN UNA BOMBA O MOTOR EN REGIMEN CONTINUO.
DESPLAZAMIENTO VOLUMÉTRICO
Una bomba tiene una característica geométrica muy importante denominada
desplazamiento volumétrico DV o volumen de expulsión definida como el volumen de
fluido que desplaza o que impulsa en una revolución ( cm3
/ rev ).
Si una bomba gira n revoluciones por cada minuto el caudal que envía (recibe) será:
En el caso de un motor hidráulico se denomina Volumen Absorbido VA.
Q DV n= ×
BOMBA HIDRAULICA
característica fisica = D.V.
Q = DV.n
n
Fig. 3.4

7. Tecsup Virtu@l Mandos Hidráulicos
Pag. 5 Unidad III
Ejemplo:
Calcular del caudal ( GPM ) que impulsa una bomba de engranajes si tiene un
desplazamiento volumétrico DV de 10 cm3
por revolución y esta acoplada a un motor
eléctrico de 1800 rpm.
Solución:
Revoluciones: n RPM
rev
min min
min= = = = −
1800 1800 1800
1
1800 1
Desplazamiento Volumétrico : DV cm= 10 3
Q DV n
Q
cm
rev
rev
min
Q
cm
min
l
min
Q
l
min
Galon
l
GPM
= ×
= ×
= =
= × =
10 1800
18000 18
18
1
3 785
4 76
3
3
,
,
Aplicaciones:
• El Desplazamiento Volumétrico es el parámetro mas importante para la
selección de una bomba o motor hidráulico.
• El Desplazamiento Volumétrico es sinónimo de tamaño o Volumen:
“Una bomba pequeña tendrá un DV pequeño e impulsa poco caudal y
una bomba grande tendrá un DV grande e impulsa bastante caudal”.
• El Desplazamiento Volumétrico de una bomba o motor hidráulico se puede
determinar aproximadamente en forma práctica llenando las cavidad de la bomba
con aceite hidráulico y luego se vierte este volumen en un recipiente graduado.
Este valor se multiplica por las rpm del motor que accionará a la bomba ( Si es
eléctrico: 1800 rpm, 3600 rpm; Si es de combustión interna 1500...4000 rpm ).
Algunos catálogos toman el valor de 1500 rpm para evaluar un caudal estándar de
la bomba.
• También se puede evaluar el desplazamiento volumétrico a través de relaciones
geométricas de su estructura interna que están en función del tipo de bomba.
1.4. MEDICIÓN DEL CAUDAL
La forma más sencilla de medir el caudal es utilizando un recipiente graduado ( V )
y un cronómetro ( t ) , no obstante es recomendable emplear caudalímetros.

8. Tecsup Virtu@l Mandos Hidráulicos
Pag. 6 Unidad III
1.4.1. CAUDALÍMETRO
Instrumentos que miden el caudal
Se representan:
Fig. 3.5
Tipos:
TURBINAS DE MEDICIÓN: Sus revoluciones indican la magnitud del caudal;
es decir, las revoluciones son proporcionales al caudal.
5 4 03
n≈Q
Fig. 3.6
DIAFRAGMA: La pérdida de presión medida en el diafragma es proporcional
al cuadrado del caudal. “Un aumento en el caudal produce un aumento
cuadrático de la caida de presión”.

9. Tecsup Virtu@l Mandos Hidráulicos
Pag. 7 Unidad III
p∆
p 1
p 2
p2
∆≈Q
Fig. 3.7
Se muestra un caudalimetro de 0 ... 5 l/min cuyo principio es la caida de
presión en el elemento móvil:
Fig. 3.8
2. GENERACIÓN DE LA PRESIÓN
“La presión se origina, cuando el caudal encuentra una resistencia a su desplazamiento”.
Definiciones previas:
BOMBA OLEOHIDRÁULICA: Envía caudal al sistema.
VÁLVULA DE SEGURIDAD: Válvula que apertura (deja pasar al fluido) al valor
en presión al que ha sido regulada.
V. DE ESTRANGULAMIENTO: Genera resistencia al paso del fluido.
Se muestra una bomba que envía un caudal de 10 l/min. , tiene su salida conectada a una
válvula de seguridad regulada a 80 bar y a una válvula de apertura – cierre.
Si la válvula de apertura – cierre esta totalmente abierta, no hay resistencia; el caudal que
envía la bomba pasa libremente y la presión en el manómetro marca cero (realmente el
manómetro debe de indicar un pequeño valor debido a la fricción y a las pérdidas de energía
en la tubería).

10. Tecsup Virtu@l Mandos Hidráulicos
Pag. 8 Unidad III
BOMBA
10 l/min
VALVULA
DE
SEGURIDAD
VALVULA
APERTURA - CIERRE
0 bar
Fig. 3.9
A medida que se va cerrando la válvula, se va aumentando la resistencia al paso del fluido y
la lectura en el manómetro empezará a aumentar, si seguimos cerrando, la presión
aumentará sin límite debido a que la bomba siempre envía 10 l/min.
BOMBA
10 l/min
VALVULA
DE
SEGURIDAD
VALVULA
APERTURA - CIERRE↑p
Fig. 3.10
Pero al llegar a 80 bar, se abre la válvula de seguridad y deja pasar todo el fluido, no
dejando que la presión sobrepase este límite. Por ello es importante la válvula de seguridad
denominada realmente Válvula Limitadora de Presión.

11. Tecsup Virtu@l Mandos Hidráulicos
Pag. 9 Unidad III
BOMBA
10 l/min
VALVULA
DE
SEGURIDAD
VALVULA
APERTURA - CIERREp = 80 bar
Fig. 3.11
Cuando los fluidos se desplazan tienen varias alternativas de caminos a seguir:
2.1. SISTEMA EN PARALELO
“Cuando los caminos alternativos en paralelo ofrecen resistencias diferentes el fluido
toma el camino de menor resistencia”.
Ejemplo:
En la figura 3.12 la bomba envía 10 I/min. Las tuberías A, B y C, ofrecen resistencias
al paso del fluido de 10 bar, 30 bar, y 50 bar respectivamente.
Al tener varias alternativas de circulación el fluido pasará por el camino que menor
resistencia le ofrece, en este caso la tubería A y el manómetro marcará 10 bar.
A
C
B
OFRECE UNA RESISTENCIA
EQUIVALENTE A 10 BAR
10 bar OFRECE UNA RESISTENCIA
EQUIVALENTE A 30 BAR
OFRECE UNA RESISTENCIA
EQUIVALENTE A 50 BAR
BOMBA
FFiigg.. 33..1122

12. Tecsup Virtu@l Mandos Hidráulicos
Pag. 10 Unidad III
Si se bloquea el tubo A (Fig. 3.13), el manómetro marcará 30 bar. ( menor resistencia
entre las tuberías de las alternativas B y C ).
A
C
B
30 bar OFRECE UNA RESISTENCIA
EQUIVALENTE A 30 BAR
OFRECE UNA RESISTENCIA
EQUIVALENTE A 50 BAR
BOMBA
CERRADO
Fig. 3.13
Si se bloquea las tuberías A y B el fluido pasara por la tubería C indicando el
manómetro 50 bar.
2.2. SISTEMA EN SERIE
“Cuando hay solo un camino con diversas resistencias, las resistencias evaluadas en
términos de presión se suman”.
Ejemplo:
En este caso, la presión indicada en el manómetro es la resistencia equivalente a la
suma de las resistencias de 30 bar y 10, es decir 40 bar.

13. Tecsup Virtu@l Mandos Hidráulicos
Pag. 11 Unidad III
CB
40 bar
OFRECE UNA RESISTENCIA
EQUIVALENTE A
30 BAR
OFRECE UNA RESISTENCIA
EQUIVALENTE A
10 BAR
BOMBA
FFiigg.. 33..1144
Si se invierten las resistencias igualmente la presión indicada por el manómetro será
la suma de las dos resistencias, es decir 40 bar.
2.3. CAÍDA DE PRESIÓN
Cuando el fluido pasa por un paso restringido o cualquier elemento que le representa
resistencia, se produce una diferencia de presión (caída de presión). Se denomina
caída de presión, puesto que si un fluido circula por un orificio, la presión a la salida
del orificio, (en el sentido de la corriente), es menor que la presión a la entrada.
∆p p p= −1 2
barp
p
30
1040
=∆
−=∆
C
B
10 bar40 bar
bar30=∆p
FFiigg.. 33..1155

14. Tecsup Virtu@l Mandos Hidráulicos
Pag. 12 Unidad III
Dicha caída de presión depende principalmente de la velocidad con que circula el
fluido
2
kvp =∆
Pero influyen una serie de parámetros como:
• La viscosidad del fluido
• La temperatura del fluido
• El área (diámetro) del estrangulamiento
• El caudal que realmente circula
• La rugosidad
• La longitud
• La forma del conducto.
Ejemplo:
Si a través de la misma tubería circula mayor caudal la caída de presión aumenta.
barp
p
160
20-180
=∆
=∆
C
B
20 bar180 bar
bar160=∆p
FFiigg.. 33..1166
Lógicamente si no hay caudal, la caída de presión es cero, lo que no indica que no
exista presión.
(La presión es igual en todos los puntos de un recipiente que mantiene a un fluido en
reposo).
barp
p
0
2020
=∆
−=∆
C
B
20 bar20 bar
bar0=∆p
FFiigg.. 33..1177

15. Tecsup Virtu@l Mandos Hidráulicos
Pag. 13 Unidad III
Estos valores los podemos representar a través del gráfico:
2
kQp =∆
PÉRDIDAS ENFUNCIÓNDEL CAUDAL
0
20
40
60
80
100
120
0 1 2 3 4 5 6 7
CAUDAL ( Q)
PERDIDAS(-p)
Fig. 3.18
La generación de presión es sinónimo de energía disponible.
Las caídas de presión son sinónimos de energía pérdida.
Por efecto de las caídas de presión se condicionan los diseños, tamaños, formas, etc.
La importancia de estos temas radica en que leyendo los valores de presión
correspondientes es posible diagnosticar el funcionamiento o la falla de un sistema
hidráulico.
FIN DE LA UNIDAD