Descargado 16 veces
Subido porangel cardenas
Torsión parte 1
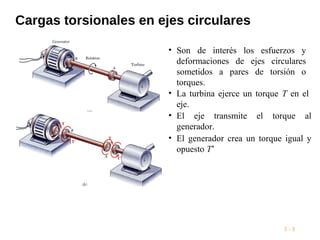
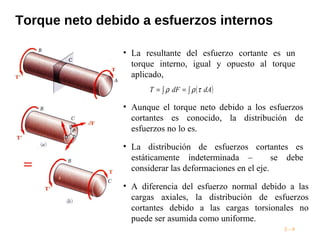
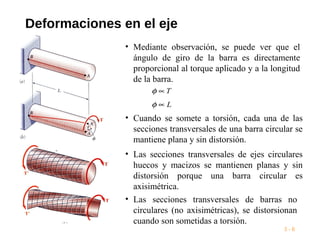
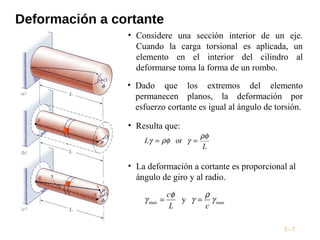
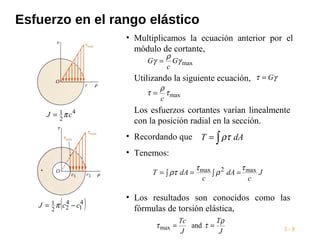
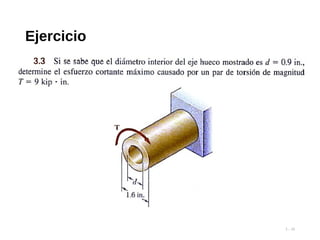
Este documento presenta conceptos clave sobre torsión en ejes circulares. Explica que un torque aplicado crea esfuerzos cortantes internos que transmiten la carga a través del eje. Las secciones transversales permanecen planas sin distorsión, mientras que las deformaciones a cortante varían linealmente con el radio. También presenta fórmulas clave para calcular esfuerzos máximos de torsión basados en el torque aplicado, momento de inercia y módulo de cortante del material.
Torsión parte 1
- 1. Libro guía: Beer F.,et al., Mecánica de Materiales, Mc Graw Hill, 6ta Edición, 2012. Notas de clase realizadas por: J. Walt Oler Texas Tech University Traducidas y modificadas por: M.I. Jónatan Pozo Palacios Universidad Politécnica Salesiana Torsión
- 2. Contenidos 3 - 2 Introducción Cargastorsionales en ejes circulares Torque neto debido a esfuerzos internos Componentes de cortante axial Deformaciones en el eje Deformación a cortante Esfuerzo en el rango elástico
- 3. Cargas torsionales enejes circulares 3 - 3 • Son de interés los esfuerzos y deformaciones de ejes circulares sometidos a pares de torsión o torques. • El generador crea un torque igual y opuesto T’ • El eje transmite el torque al generador. • La turbina ejerce un torque T en el eje.
- 4. Torque neto debidoa esfuerzos internos 3 - 4 ( )∫ ∫== dAdFT τρρ • La resultante del esfuerzo cortante es un torque interno, igual y opuesto al torque aplicado, • Aunque el torque neto debido a los esfuerzos cortantes es conocido, la distribución de esfuerzos no lo es. • A diferencia del esfuerzo normal debido a las cargas axiales, la distribución de esfuerzos cortantes debido a las cargas torsionales no puede ser asumida como uniforme. • La distribución de esfuerzos cortantes es estáticamente indeterminada – se debe considerar las deformaciones en el eje.
- 5. Componentes de cortanteaxial 3 - 5 • El torque aplicado a un eje produce esfuerzos cortantes en las caras perpendiculares al eje. • La existencia de los componentes de cortante axial es demostrado al considerar un eje hecho de tablillas axiales. Las tablillas axiales se deslizan entre ellas cuando torques iguales y opuestos son aplicados en los extremos del eje. • Las condiciones de equilibrio requieren de la existencia de esfuerzos iguales en las caras de los dos planos que contienen al eje de la barra.
- 6. Deformaciones en eleje 3 - 6 • Mediante observación, se puede ver que el ángulo de giro de la barra es directamente proporcional al torque aplicado y a la longitud de la barra. L T ∝ ∝ φ φ • Cuando se somete a torsión, cada una de las secciones transversales de una barra circular se mantiene plana y sin distorsión. • Las secciones transversales de barras no circulares (no axisimétricas), se distorsionan cuando son sometidas a torsión. • Las secciones transversales de ejes circulares huecos y macizos se mantienen planas y sin distorsión porque una barra circular es axisimétrica.
- 7. Deformación a cortante 3- 7 • Considere una sección interior de un eje. Cuando la carga torsional es aplicada, un elemento en el interior del cilindro al deformarse toma la forma de un rombo. • La deformación a cortante es proporcional al ángulo de giro y al radio. maxmax y γ ρ γ φ γ cL c == L L ρφ γρφγ == or • Resulta que: • Dado que los extremos del elemento permanecen planos, la deformación por esfuerzo cortante es igual al ángulo de torsión.
- 8. Esfuerzo en elrango elástico 3 - 8 J c dA c dAT max2max τ ρ τ ρτ ∫ =∫ == • Recordando que • Tenemos: 4 2 1 cJ π= ( )4 1 4 22 1 ccJ −= π andmax J T J Tc ρ ττ == • Los resultados son conocidos como las fórmulas de torsión elástica, • Multiplicamos la ecuación anterior por el módulo de cortante, maxγ ρ γ G c G = maxτ ρ τ c = Utilizando la siguiente ecuación, γτ G= Los esfuerzos cortantes varían linealmente con la posición radial en la sección. ∫= dAT ρτ
- 9.
- 10.
- 11.
- 12.