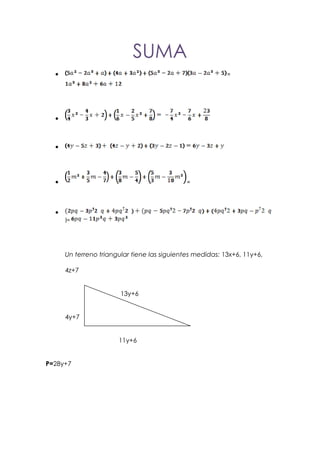
Este documento explica conceptos básicos de álgebra como términos algebraicos, expresiones algebraicas, polinomios y ecuaciones algebraicas. Define álgebra como el estudio de cómo resolver ecuaciones y explica que utiliza símbolos para representar números. También cubre temas como coeficientes, variables, exponentes, sumas, restas, multiplicaciones y divisiones algebraicas.

1. CEDART <br />David Alfaro Siqueiros<br />ÁLGEBRA<br />Dyana Samantha Corrales Gutiérrez<br />1A<br />INTRODUCCIÓN<br />El término álgebra viene del título de la obra del mátematico árabe Mahommed ibn Musa al-Kharizmi, que significa Mahommed, hijo de Musa, natural de Kharizm, al-jebr w'al-muqabalah, que significa transposición y eliminación.<br />El álgebra es una rama de las Matemáticas que estudia la forma de resolver las ecuaciones.<br />Una de las características del álgebra es que utiliza símbolos para representar números.<br />El álgebra actual trata con entidades mas generales que los números y sobre estas entidades define operaciones (similares a las operaciones aritméticas). Esta nueva álgebra se debe a Galois.<br />USOS<br />Aunque parezca no tener un servicio práctico, el álgebra y el estudio general de las matemáticas te dan una gran capacidad de análisis y de facilidad a la hora de resolver cualquier problema de la vida cotidiana. Te da una capacidad de razonamiento mas elevada. <br />TÉRMINOS ALGEBRÁICOS<br />Un término algebraico consta de las siguientes partes:<br />Signo. Puede ser positivo (+), o negativo (-). <br />Coeficiente. En el producto de dos o más factores, cualquiera de ellos puede llamarse coeficiente de los otros factores <br />Ejemplo: <br />En 7ab2c ; 7 es coeficiente de ab2ca es coeficiente de 7b2c b2 es coeficiente de 7acc es coeficiente de 7ab2<br />En general, se le llama coeficiente a una constante (con todo y signo), que es un factor de las variables de cualquier término algebraico. <br />Variable (o parte literal). Cantidad generalizada. <br />Exponente. Es el número de veces que se multiplicará la cantidad generalizada o variable, por sí misma. <br />Ejemplos: <br />a) -2x2;Signo: negativoCoeficiente: -2Variable: xExponente: 2 b) ax2y3;Signo: positivoCoeficiente: aVariables: x , yExponentes: 2 (de la x)3 (de la y)<br />EXPRESIÓN ALGEBRÁICA<br />Antes veamos lo que es una expresión aritmética. Una expresión aritmética es una cadena de símbolos (números y signos de operación), que indican una cantidad finita de operaciones básicas entre dichos números. Las operaciones básicas son la suma, resta, multiplicación y división. <br />Una expresión algebráica es una cadena de símbolos matemáticos que indican una cantidad finita de operaciones básicas entre funciones elementales, como raíces, exponenciales, logaritmos, funciones trigonométricas y también composiciones de dichas funciones. Suena muy revuelto pero como ejemplo veamos las siguientes tres expresiones: <br />En estas expresiones vemos involucrados: números y letras sumados, multiplicados, divididos, con exponentes de varios tipos, con raíces cuadradas y hasta logaritmos; así de complejas pueden ser las expresiones algebráicas. Pero lo complicado de una expresión algebráica es: imaginemos que tuvieramos a la mano una calculadora, y se nos pidiera hallar el resultado final de la siguiente expresión algebráica si x = 125. <br />¿Por dónde empezamos a hacer las cuentas? Es decir, ¿En qué orden? Para responder esta pregunta, necesitaremos conocer los elementos de las expresiones algebráicas, y establecer un orden para las operaciones: <br />EXPONENTES<br />Son los superíndices que afectan a los diversos términos de las expresiones. <br />Son ciertas partes que componen una expresión algebráica que en los polinomios se identifican muy fácilmente, pero no así en otras expresiones. <br />Los polinomios resultan ser expresiones algebráicas muy importantes y los definimos a continuación. <br />Un polinomio de grado “n” es una expresión algebráica de la forma donde “n” es un número natural, las 's son números reales y se dice que es de grado “n” porque es el exponente mas grande que aparece. A las 's se les llama coeficientes del polinomio. <br />GRADO<br />En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de que se trate. Todas las definiciones tienen como resultado un número natural que expresa el grado.<br />GRADO DE UN POLINOMIO<br />El grado de un polinomio de una variable es el máximo exponente que posee el monomio sobre la variable; Por ejemplo en 2x3 + 4x2 + x + 7, el término de mayor grado es 2x3; este término tiene una potencia tres en la variable x, y por lo tanto se define como grado 3 o de tercer grado.<br />Para polinomios de dos o más variables, el grado de un término es la suma de los exponentes de las variables en el término; el grado del polinomio será el monomio de mayor grado. Por ejemplo, el polinomio x2y2 + 3x3 + 4y tiene un grado 4, el mismo grado que el término x2y2.<br />TEORÍA DE ESCUACIONES<br />En teoría de ecuaciones algebráicas, el grado de una ecuación corresponde a la máxima potencia a la que está elevada la incógnita algebraica de la ecuación. Por ejemplo: la ecuación es de tercer grado en x, siendo de primer grado en la incógnita y. Véase: Ecuación de segundo grado, Ecuación de tercer grado, Ecuación de cuarto grado, Ecuación de quinto grado, etc.<br />SUMA<br /> QUOTE = QUOTE

2. QUOTE

3. QUOTE

4. QUOTE =

5. QUOTE )= QUOTE Un terreno triangular tiene las siguientes medidas: 13x+6, 11y+6, 4z+7<br /> 13y+6<br />4y+7<br /> 11y+6<br />P=28y+7<br />RESTA <br />Ejemplifica una aplicación de la resta algebráica (Descubre el problema, agrega imagen o esquema y resuelve)<br /> QUOTE QUOTE <br /> QUOTE QUOTE <br /> QUOTE QUOTE <br /> QUOTE QUOTE <br /> QUOTE QUOTE <br /> QUOTE = QUOTE <br />A un pedazo de tela rectangular se le quiere quitar una parte de su perímetro para hacer su área mas pequeña. QUOTE QUOTE <br />MULTIPLICACIÓN<br />(-) (-) = +

6. (+)(+)= + Ejemplo: (-7x) (+5x) = - QUOTE

7. (-)(+)= -

8. (+)(-)= -

9. La ley distributiva dice que multiplicar una suma por un número da el mismo resultado que multiplicar cada uno por el número y después sumar todos los productos. Ejemplo: 4 x (2 +3)= 4x2+4x3

10. Los exponentes: en la multiplicación los exponentes de las mismas literales se suman.

11. División: Los exponentes de las mismas literales se suman, si queda residuo se indica donde estaba el mayor.

12. Potencia: La potencia de un número está indicada por un exponente. El número se multiplica las veces que indica el exponente