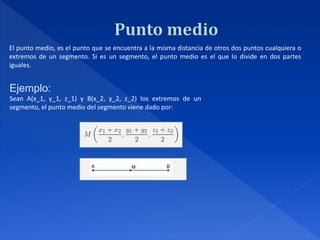
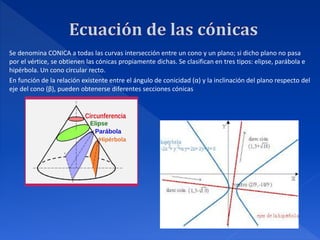
1) El documento explica cómo determinar la distancia entre dos puntos en el plano cartesiano y define el punto medio de un segmento. 2) Describe las ecuaciones para representar funciones lineales, parábolas, hipérbolas, circunferencias y elipses en el plano cartesiano. 3) Explica los elementos básicos de curvas como la circunferencia, parábola, elipse, hipérbola y cómo se definen mediante ecuaciones.

2. A partir de conocer la ubicación de dos puntos en el plano cartesiano, es posible determinar la
distancia que hay entre éstos. Cuando algún punto se encuentra en el eje de las x o de las abscisas o en
una recta paralela a éste eje, la distancia entre los puntos corresponde al valor absoluto de las
diferencia de sus abscisas. (x 2 – x 1 ).
Ejemplo:
La distancia entre los puntos (–4, 0) y (5, 0).
Donde (-4) = x 1 ; 5 = x 2. Aplicando la fórmula es 5 – (–4) = 5 +4 = 9 unidades.

3. El punto medio, es el punto que se encuentra a la misma distancia de otros dos puntos cualquiera o
extremos de un segmento. Si es un segmento, el punto medio es el que lo divide en dos partes
iguales.
Ejemplo:
Sean A(x_1, y_1, z_1) y B(x_2, y_2, z_2) los extremos de un
segmento, el punto medio del segmento viene dado por:

4. En las ecuaciones se sustituyen ciertos valores, para definir los puntos que seguirá la gráfica. Es
importante destacar, que las funciones pueden variar mucho una de otra, por lo tanto, es
necesario identificar con cual tipo de ecuación se está trabajando. Recuerda que existen
ecuaciones para funciones lineales, parábolas, hipérbolas, circunferencias, elipses, entre otras.
Lo primero que debes tener en cuenta para representan las ecuaciones en el plano cartesiano
Es que todo se fundamente en el par ordenado. Este se define sustituyendo un valor
independiente en la ecuación y consiguiendo así la variable dependiente. Seguidamente, se
organizan y se representan en el plano cartesiano.
Una vez que se hayan representados todos los pares ordenados en el plano cartesiano, es
necesarios empezar a unirlos. Para ello, es importante que sigas el orden que seguiste para
calcular los pares ordenados. Como resultado, conseguirás la gráfica correspondiente a la
ecuación de la función desarrollada

5. La circunferencia es el lugar geométrico de los puntos del plano cartesiano que equidistan de un
punto fijo llamado centro. Una circunferencia queda determinada cuando conocemos: Tres
puntos de la misma, equidistantes del centro, El centro y el radio, El centro y un punto en ella, El
centro y una recta tangente a la circunferencia.
También podemos decir que la circunferencia es la línea formada por todos los puntos que están
a la misma distancia de otro punto, llamado centro .Esta propiedad es la clave para hallar la
expresión analítica de una circunferencia. Entonces, entrando en el terreno de la Geometría
Analítica , (dentro del Plano Cartesiano ) diremos que para cualquier punto, P (x, y) , de una
circunferencia cuyo centro es el punto C (a, b) y con radio r ─, la ecuación ordinaria es(x ─ a) 2 +
(y ─ b) 2 = r 2
Ejemplo:

6. En el Plano Cartesiano una parábola puede tener su vértice en cualquier par de coordenadas y
puede estar orientada hacia arriba, hacia abajo o hacia la izquierda o la derecha.
Ecuaciones de la parábola con vértice en el origen
Primeramente, estudiaremos la ecuación de la parábola para los casos en que su vértice esté en
el origen, y según esto, tenemos cuatro posibilidades de ecuación y cada una es característica.
Para iniciar nuestra explicación empezaremos con la parábola cuyo vértice está en el origen, su
eje focal o de simetría coincide con el eje de las X (abscisas) y que está orientada (se abre) hacia
la derecha. Por definición, sabemos que, en una parábola la distancia entre un punto “P” (no
confundir con el “parámetro p”), cualquiera de coordenadas (x, y), y el foco “F” será igual a la
distancia entre la directriz (D) y dicho punto, como vemos en la figura:

7. Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es
constante.
Elementos de la elipse:
1. Focos: Son los puntos fijos F y F'.
2. Eje focal: Es la recta que pasa por los focos.
3. Eje secundario: Es la mediatriz del segmento FF'.
4. Centro: Es el punto de intersección de los ejes.
5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.
6. Distancia focal: Es el segmento segmento de longitud 2c, c es el valor de la semidistancia focal.
7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.
8. Eje mayor: Es el segmento segmento de longitud 2a, a es el valor del semieje mayor.
9. Eje menor: Es el segmento segmento de longitud 2b, b es el valor del semieje menor.
10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.
11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de
simetría.

8. La hipérbola es una curva plana, abierta, con dos ramas; se define como el lugar geométrico de los
puntos cuya diferencia de distancias a otros dos fijos, llamados focos, es constante e igual a 2a = AB, la
longitud del eje real. Tiene dos ejes perpendiculares que se cortan en el punto medio O, centro de la
curva. El eje mayor AB se llama eje real y se representa por 2a; el eje menor se representa por 2b y se
llama imaginario porque no tiene puntos comunes con la curva. Los focos están en el eje real. La
distancia focal se representa por 2c.
Entre a, b y c existe la relación c2 = a2 + b2.
La hipérbola es simétrica respecto de los dos ejes y, por lo tanto respecto del centro O. Las rectas que
unen un punto M de la curva con dos focos, se llaman radios vectores r y r' y por definición se verifica: r -
r' = 2a.
La circunferencia principal de la hipérbola es la que tiene por centro O y radio 2a. Se define como el lugar
geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes. Las
circunferencias focales tienen por centro los focos y radio a.

9. Se denomina CONICA a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa
por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en tres tipos: elipse, parábola e
hipérbola. Un cono circular recto.
En función de la relación existente entre el ángulo de conicidad (α) y la inclinación del plano respecto del
eje del cono (β), pueden obtenerse diferentes secciones cónicas