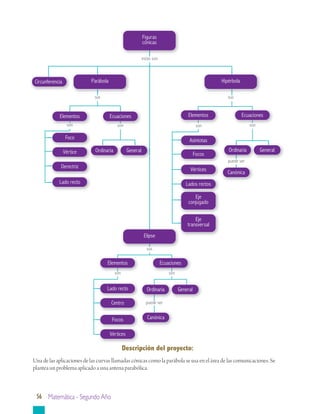
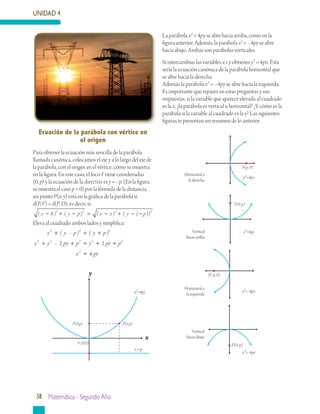
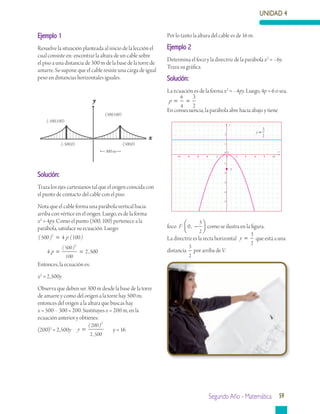
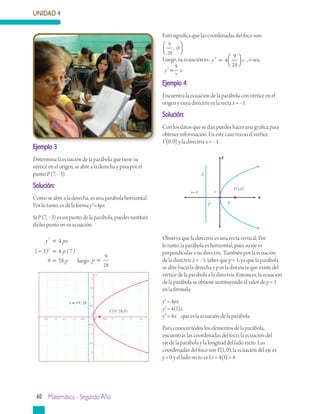
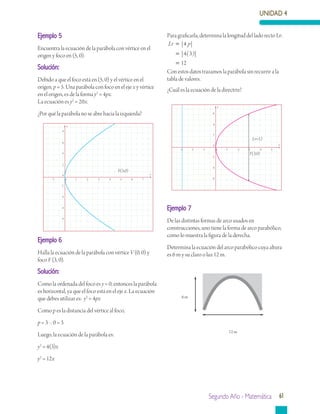
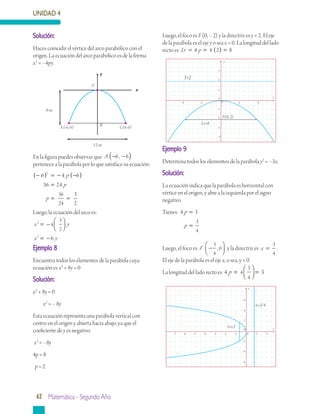
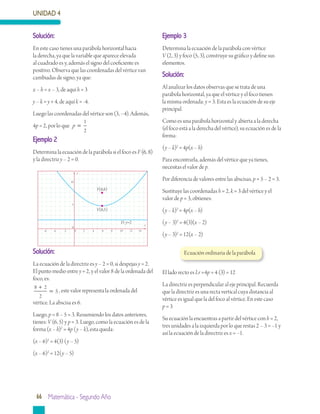
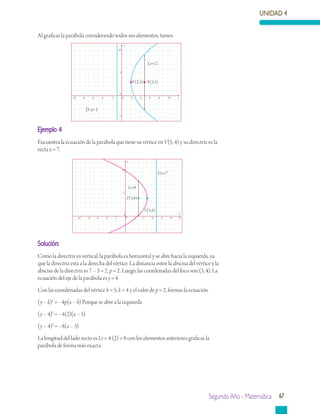
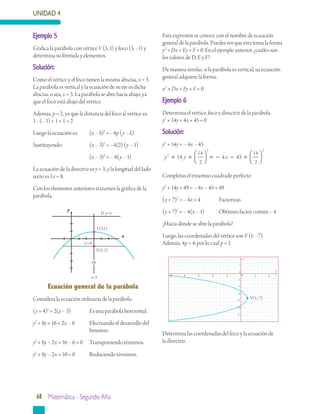
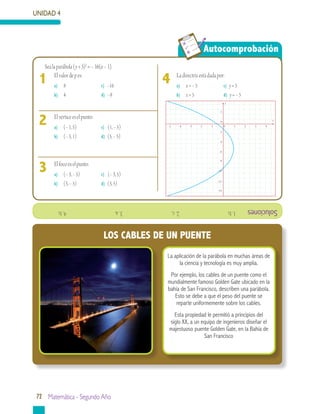
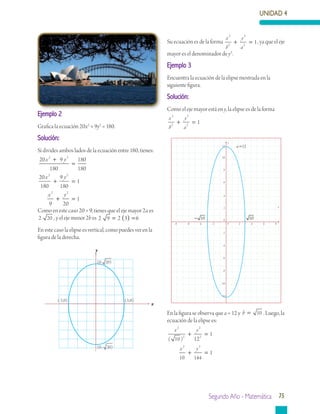
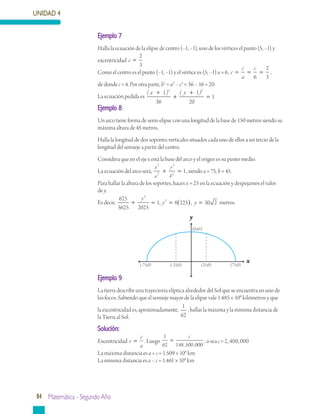
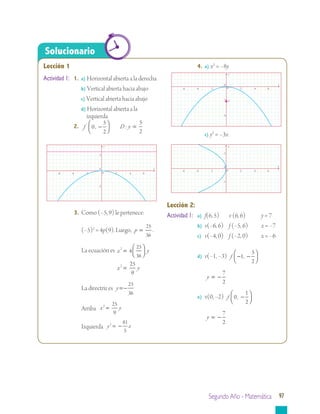
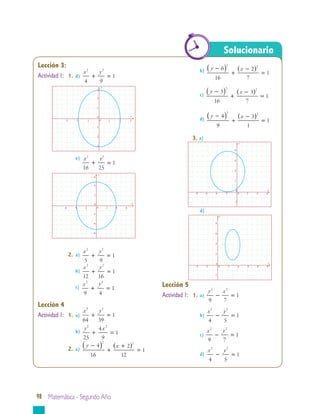
Este documento presenta información sobre geometría analítica, en particular sobre curvas cónicas como la parábola, elipse e hipérbola. Explica cómo construir y encontrar la ecuación de una parábola dados sus elementos como el vértice, foco y directriz. También incluye ejemplos resueltos sobre cómo aplicar estas ideas para resolver problemas relacionados con parábolas.