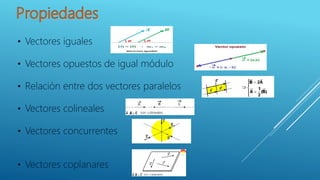
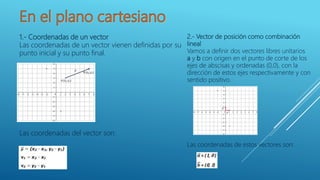
El documento aborda conceptos fundamentales sobre vectores, incluyendo dirección, sentido, magnitud y sus diferentes tipos, como vectores paralelos y colineales. Se explican las coordenadas de un vector y el vector de posición, así como las operaciones de suma, resta y multiplicación de vectores con escalares. Además, se menciona cómo las coordenadas de un vector corresponden a su representación en el plano cartesiano.

2. Segmento de recta que tiene
dirección y sentido

3. • Módulo o magnitud
• Dirección
• Sentido

4. • Vectores iguales
• Vectores opuestos de igual módulo
• Relación entre dos vectores paralelos
• Vectores colineales
• Vectores concurrentes
• Vectores coplanares

5. 1.- Coordenadas de un vector
Las coordenadas de un vector vienen definidas por su
punto inicial y su punto final.
Las coordenadas del vector son:
2.- Vector de posición como combinación
lineal
Vamos a definir dos vectores libres unitarios
a y b con origen en el punto de corte de los
ejes de abscisas y ordenadas (0,0), con la
dirección de estos ejes respectivamente y con
sentido positivo.
Las coordenadas de estos vectores son:

6. 3.- Vectores con igual dirección
Dos vectores p y q tienen la misma dirección (son paralelos) cuando sus
coordenadas son proporcionales.
4.-Vector de posición
Cualquier punto del plano cartesiano viene identificado por un vector libre diferente con inicio en el
origen de coordenadas (0,0) y final en dicho punto. Este punto se denomina vector de posición.
Podemos ver que son diferentes porque se diferencian en el módulo, en la dirección o en el sentido.
Podemos ver como las coordenadas de cada vector posición coinciden con las coordenadas del
punto que identifican.

7. • Suma de vectores
Si se suman dos magnitudes
escalares, basta con sumar sus
valores numéricos.
Conociendo las componentes
cartesianas de los vectores a sumar,
el vector resultante tendrá como
componentes cartesianos la suma,
eje a eje, de cada vector.
Si queremos sumar dos vectores en
3D y conocemos sus componentes,
las componentes del vector suma,
aplicando el mismo procedimiento,
sería:
• Resta de vectores
Se procede igual que en la suma, bien
operando con las componentes
cartesianas, o bien mediante el
método del paralelogramo.
Sabiendo los componentes
cartesianos de los vectores,
restaremos los componentes
cartesianos del segundo vector de los
del primero:
• Multiplicación de vectores
Producto de un vector por un escalar
La multiplicación de un vector v por
un escalar n es otro vector nv cuyo
módulo será |n| · |Vectorv|.
Si n es positivo, el vector producto
tendrá el mismo sentido. Si n es
negativo, el vector producto tendrá el
sentido opuesto.
Lo mismo diremos de la división de un
vector por un escalar.