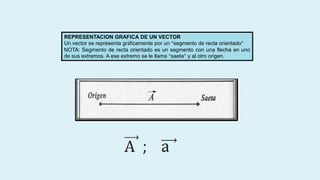
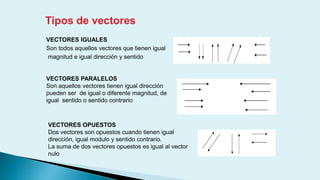
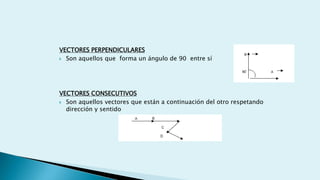
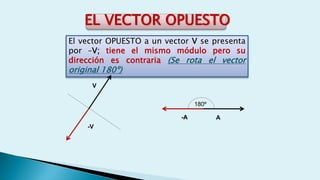
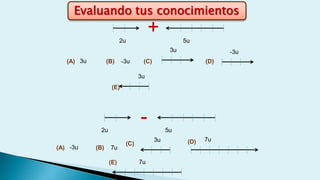
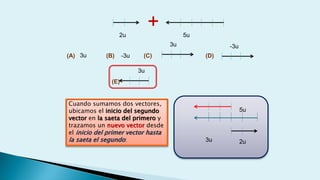
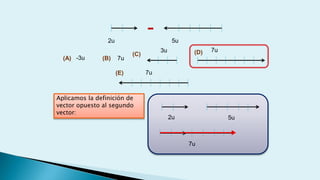
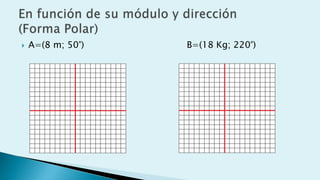
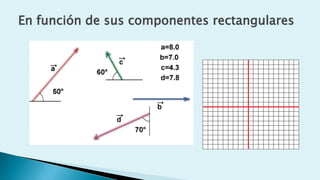
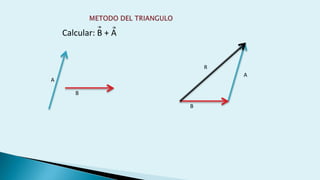
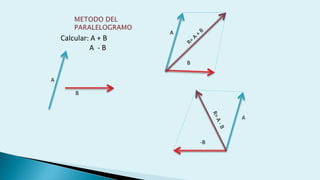
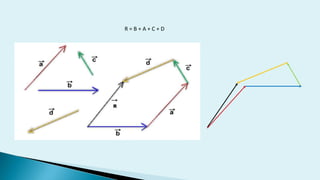
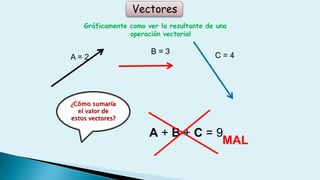
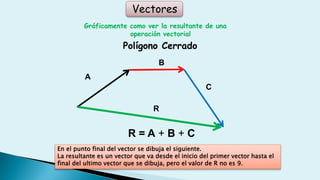
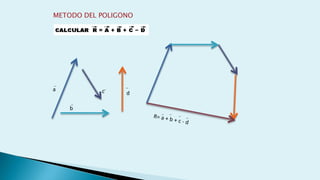
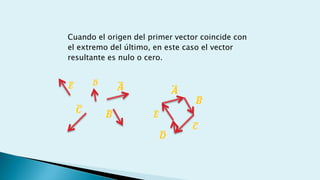
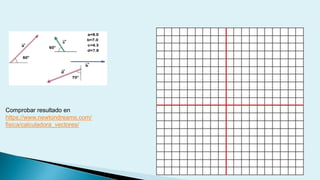
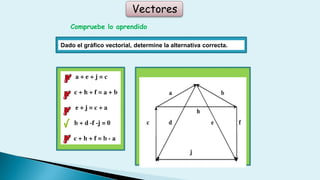
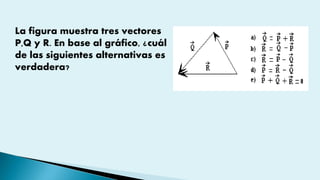
Este documento describe conceptos básicos de vectores en mecánica, incluyendo que un vector se especifica por magnitud y dirección, y se representa gráficamente como un segmento de recta orientado. También cubre operaciones con vectores como suma, resta, vectores paralelos y perpendiculares.

1. Física Mecánica

2.  Las operaciones entre cantidades escalares deben
ser coherentes; es decir las cantidades deben tener
las mismas unidades para poder operarse.
EJEMPLOS:
 30kg+40kg=70kg
 20s+43s=63s
 20m+40m=60m

3. CANTIDADES VECTORIALES:
 Una cantidad vectorial se especifica totalmente por una
magnitud y una dirección, consiste en un número, unidad,
dirección y sentido.
 Las magnitudes vectoriales se representan gráficamente
mediante un segmento de recta dirigido llamado vector.
EJEMPLOS:
 Velocidad: V
 Aceleración: a
 Fuerza : f
 Velocidad: 108 km/h,120°
 Aceleración: 3m/s2,120°
 Fuerza : 50N (N 45° E)
 Desplazamiento: 30m ( S 50° E)

4. REPRESENTACION GRAFICA DE UN VECTOR
Un vector se representa gráficamente por un “segmento de recta orientado”
NOTA: Segmento de recta orientado es un segmento con una flecha en uno
de sus extremos. A ese extremo se le llama “saeta” y al otro origen.

5. CARACTERÍSTICAS DE UN VECTOR
EJE X
SENTIDO
MÓDULO
O
MAGNITUD
DIRECCIÓN


6. VECTORES IGUALES
Son todos aquellos vectores que tienen igual
magnitud e igual dirección y sentido
Tipos de vectores
VECTORES PARALELOS
Son aquellos vectores tienen igual dirección
pueden ser de igual o diferente magnitud, de
igual sentido o sentido contrario
VECTORES OPUESTOS
Dos vectores son opuestos cuando tienen igual
dirección, igual modulo y sentido contrario.
La suma de dos vectores opuestos es igual al vector
nulo

7. VECTORES PERPENDICULARES
 Son aquellos que forma un ángulo de 90 entre sí
VECTORES CONSECUTIVOS
 Son aquellos vectores que están a continuación del otro respetando
dirección y sentido

8.  VECTOR RESULTANTE
 En un sistema de vectores es un vector único que produce los
mismos efectos que todos los vectores dados.

10. OPERACIONES CON
VECTORES:

11. SUMA DE VECTORES PARALELOS DE
IGUAL DIRECCIÓN Y SENTIDO
Hallar A+B
Hallar A+B

12. EL VECTOR OPUESTO
El vector OPUESTO a un vector V se presenta
por –V; tiene el mismo módulo pero su
dirección es contraria (Se rota el vector
original 180º)
V
-V
A-A
180º

13. RESTA DE VECTORES PARALELOS
DE IGUAL DIRECCION Y SENTIDO
Hallar A-B
Hallar A-B

14. SUMA Y RESTA DE VECTORES
PARALELOS DE SENTIDO CONTRARIO

15. 2u
+ 5u
(A) 3u (B) -3u (C)
3u
(D)
-3u
3u
(E)
2u
- 5u
(A) -3u (B) 7u
(C) (D) 7u3u
(E) 7u
Evaluando tus conocimientos

16. 2u
+ 5u
(A) 3u (B) -3u (C)
3u
(D)
-3u
3u
(E)
Cuando sumamos dos vectores,
ubicamos el inicio del segundo
vector en la saeta del primero y
trazamos un nuevo vector desde
el inicio del primer vector hasta
la saeta el segundo: 2u
5u
3u

17. 2u
- 5u
(A) -3u (B) 7u
(C) (D) 7u3u
(E) 7u
Aplicamos la definición de
vector opuesto al segundo
vector:
2u 5u
7u

19.  A=(8 m; 50°) B=(18 Kg; 220°)

20. En función de sus componentes rectangulares

21. Suma de
vectores no
paralelos

23. Como su nombre lo indica consiste en
formar la figura del triángulo, el método se
basa en graficar los vectores dados en
forma consecutiva respetando magnitud
dirección y sentido, el vector resultante en
aquel que parte del pie del primer vector y
termina en la saeta del otro vector.

24. Calcular: B + A
A
B
A
B
R

26. Consiste en tener los dos vectores dados
concurrentes, se trazan rectas paralelas a
cada vector formando la figura
paralelogramo. La diagonal de la figura es el
vector resultante.

27. Calcular: A + B
A - B
A
B
B
A
-B
A

29. El método del polígono cerrado consiste en
dibujar un vector a continuación de otro. El
inicio de cada vector debe coincidir con el final
del último vector graficado. El vector resultante
o suma es aquel que va desde el origen del
primer vector graficado hasta el final (saeta)
del último vector graficado.

30. R = B + A + C + D

31. Vectores
Gráficamente como ver la resultante de una
operación vectorial
A = 2
B = 3 C = 4
¿Cómo sumaría
el valor de
estos vectores?
A + B + C = 9
MAL

32. Vectores
Gráficamente como ver la resultante de una
operación vectorial
A
B
C
En el punto final del vector se dibuja el siguiente.
La resultante es un vector que va desde el inicio del primer vector hasta el
final del ultimo vector que se dibuja, pero el valor de R no es 9.
R = A + B + C
R
Polígono Cerrado

33. METODO DEL POLIGONO
a
b
c d

34. Cuando el origen del primer vector coincide con
el extremo del último, en este caso el vector
resultante es nulo o cero.

35. Hallar el vector resultante de la suma de los vectores
mostrados en la figura

36. Comprobar resultado en
https://www.newtondreams.com/
fisica/calculadora_vectores/

39. Vectores
Compruebe lo aprendido
Los vectores A, B y C se muestran en la figura, cuyas magnitudes
son de 10, 15 y 20 unidades respectivamente. El valor del vector
A – B – C es:
a) 5 unidades, hacia la
derecha
b) 25 unidades, hacia la
izquierda
c) 25 unidades, hacia la
derecha
d) 40 unidades, hacia la
derecha
e) 5 unidades, hacia la
izquierda

40. Vectores
Compruebe lo aprendido
En la figura se representa cinco vectores sobre una escala
cuadriculada. Determine si las proposiciones son verdaderas (V) o
falsas (F).

41. Vectores
Compruebe lo aprendido
Dado el gráfico vectorial, determine la alternativa correcta.

42. La figura muestra tres vectores
P,Q y R. En base al gráfico, ¿cuál
de las siguientes alternativas es
verdadera?