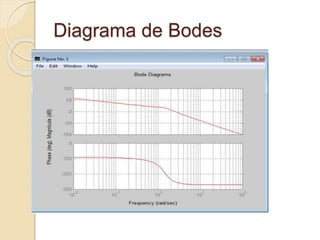
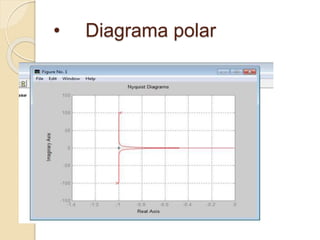
Este documento presenta tres diagramas relacionados con la respuesta en frecuencia: el diagrama de Bode, que muestra la magnitud y fase de una función de transferencia en escala logarítmica; el diagrama polar o de Nyquist, que representa paramétricamente una función de transferencia; y usa Matlab para generar ejemplos de estos diagramas.

1. INSTITUTO UNIVERSITARIO POLITECNICO
“SANTIAGO MARIÑO”
EXTENSIÓN PORLAMAR
Respuesta en Frecuencia
Realizado por:
Williams Enrique Suarez Bermúdez
CI:12.658.254
Porlamar19/07/2014

2. Introducción Hoy en dia contamos con serie de software o programas que nos facilitan
los diferentes análisis de los cálculos matemáticos, tal es el caso de matlab,
que es una herramienta para el calculo y simulacion de problemas
matematicos.
 MATLAB dispone también en la actualidad de un amplio abanico
de programas de apoyo especializado, denominados Toolboxes, que
extienden significativamente el número de funciones incorporadas en el
programa principal. Estos Toolboxes cubren en la actualidad prácticamente
casi todas las áreas principales en el mundo de la ingeniería y la
simulación, destacando entre ellos el 'toolbox' de proceso de imágenes,
señal, control robusto, eestadística,
análisis financiero, matemáticas simbólicas, redes neutrales, lógica difusa,
identificación de sistemas, simulación de sistemas dinámicos, etc.
 En el siguiente informe mostraremos una serie de diagramas , relacionados
con la Respuesta en frecuencia, entre ellos tenemos el Diagrama de Bodes,
el cual muestra un trazado de de un diagrama logarítmico de la función de
transferencia sinoidal y un diagrama del Angulo de fase , ambos
representado en una función de la frecuencia en escalas logarítmicas.

3. Por otro lado tenemos los diagramas polares o nyquist .
El diagrama polar de una función de transferencia sinusoidal G(jw) es una
gráfica de la magnitud de G(jw) con respecto al ángulo de fase de G(jw) en
coordenadas polares, cuando “w” varía de cero a infinito. Por tanto, el
diagrama polar es el lugar geométrico de los vectores G( jw)∠G( jw) cuando
“w” varía de cero a infinito. Cada punto en el diagrama polar de G(jw)
representa el punto terminal de un vector en un valor determinado “w”. En el
diagrama polar, es importante mostrar la graduación de la frecuencia del lugar
geométrico. Las proyecciones de G(jw) en los ejes real e imaginario son sus
componentes real e imaginaria. En las gráficas polares, los ángulos de fase
son positivos (negativos) si se miden en el sentido contrario al de las
agujas del reloj (en el sentido de las agujas) a partir del eje real positivo. El
diagrama polar se denomina, a menudo, “Diagrama de Nyquist”

4. Desarrollo
 Diagrama de bode. ejemplo 1
 Dibuje el diagrama de bode para la
siguiente función de transferencia:
 G(s) = 10(jw+3) /
(jw)(jw+2)[(jw)2+jw+2]

5. Código del Programa

6. Diagrama de Bodes

7. Diagrama polar o NYQUIST. ejemplo 2
Considere la siguiente función de
transferencia de segundo orden:
G(s) = 1/s(Ts+1)

8. Código de programación

9. • Diagrama polar o
NYQUIST

10. Diagrama polar o NYQUIST. ejemplo
3
Obtenga el diagrama polar de la
siguiente transferencia:
G(jw)= e-jwl/1+jwl

11. Código de Programación

12. • Diagrama polar

13. Conclusión
Los diagramas de bodes , podemos resumir que son una representación
gráfica que sirve para caracterizar la respuesta en frecuencia de un sistema.
Normalmente consta de dos gráficas separadas, una que corresponde con la
magnitud de dicha función y otra que corresponde con la fase.
El diagrama de magnitud de Bode dibuja el módulo de la función de
transferencia (ganancia) en decibelios en función de la frecuencia (o la
frecuencia angular) en escala logarítmica. Se suele emplear en procesado de
señal para mostrar la respuesta en frecuencia de un sistema lineal e invariante
en el tiempo.
El diagrama de fase de Bode representa la fase de la función de transferencia
en función de la frecuencia (o frecuencia angular) en escala logarítmica. Se
puede dar en grados o en radianes. Permite evaluar el desplazamiento en fase
de una señal a la salida del sistema respecto a la entrada para una frecuencia
determinada.
Por otro lado los diagramas Polar o Nysquist, sirven para

14. Para representar paramétricamente una función de transferencia, se utiliza
en control automático y procesamiento de señales. El uso más común de los
diagramas de Nyquist es para la evaluación de la estabilidad de un sistema
con realimentación. La representación en los ejes cardinales es, la parte real
de la función de transferencia se representa en el eje X, la parte imaginaria
se traza en el eje Y. La frecuencia se recorre como un parámetro, por lo que
a cada frecuencia le corresponde un punto de la gráfica. Alternativamente,
en coordenadas polares, la ganancia de la función de transferencia se
representa en la coordenada radial, mientras que la fase de la función de
transferencia se representa en la coordenada angular.
También podemos agregar que gracias a Matlab se hace mas fácil el
análisis de estos diagramas.