Regresion lineal

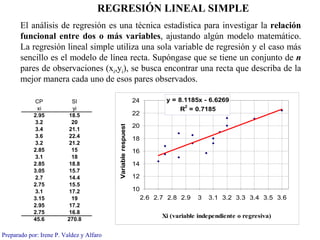
REGRESIÓN LINEAL SIMPLE
El análisis de regresión es una técnica estadística para investigar la relación
funcional entre dos o más variables, ajustando algún modelo matemático.
La regresión lineal simple utiliza una sola variable de regresión y el caso más
sencillo es el modelo de línea recta. Supóngase que se tiene un conjunto de n
pares de observaciones (xi,yi), se busca encontrar una recta que describa de la
mejor manera cada uno de esos pares observados.

CP SI 24 y = 8.1185x - 6.6269
2
xi yi R = 0.7185
2.95 18.5 22
3.2 20 Variable respuest 20
3.4 21.1
3.6 22.4 18
3.2 21.2
2.85 15 16
3.1 18
2.85 18.8 14
3.05 15.7
2.7 14.4 12
2.75 15.5
3.1 17.2 10
3.15 19 2.6 2.7 2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6
2.95 17.2
2.75 16.8
Xi (variable independiente o regresiva)
45.6 270.8

Preparado por: Irene P. Valdez y Alfaro

Se considera que la variable X es la variable
independiente o regresiva y se mide sin error,
mientras que Y es la variable respuesta para cada
valor específico xi de X; y además Y es una variable
aleatoria con alguna función de densidad para cada
nivel de X.

f (Y xi )

Y xi
yi
E (Y xi )

Regresión Lineal Simple
yi = β 0 + β1 xi + ε i
f (Y xi )

E (Y xi ) = β 0 + β1 xi

x 1 xi xn
Si la recta de regresión es: Y = β 0 + β1 X
Cada valor yi observado para un xi puede considerarse como el valor
esperado de Y dado xi más un error:
Modelo lineal simple : yi = β 0 + β1 xi + ε i
Los εi se suponen errores aleatorios con distribución normal,
media cero y varianza σ2 ; β0 y β1 son constantes desconocidas
(parámetros del modelo de regresión)

Método de Mínimos Cuadrados
para obtener estimadores de β0 y β1
Consiste en determinar aquellos estimadores de β0 y β1 que
minimizan la suma de cuadrados de los errores εi ; es decir,
los estimadores β 0 y β1 de β0 y β1 respectivamente deben
ˆ ˆ
ser tales que: n
2
∑εi sea mínima.
i =1

Del modelo lineal simple: yi = β 0 + β1 xi + ε i
de donde: ε i = yi − β 0 − β1 x
n 2 n
2
elevando al cuadrado: ∑ ε i = ∑ ( yi − β 0 − β1 x)
i =1 i =1


Según el método de mínimos cuadrados, los
estimadores de β0 y β1 debe satisfacer las
ecuaciones: n n
∂ n 2 ∑ yi = nβ 0 + β1 ∑ xi
∑ ( yi − β 0 − β1 x) = 0 Al derivar se obtiene un i =1 i =1
∂β 0 i =1 sistema de dos ecuaciones
n n n
denominadas “ecuaciones 2
∂ n 2 normales”: β 0 ∑ xi + β 1 ∑ xi = ∑ xi yi
∑ ( yi − β 0 − β1 x) = 0 i =1 i =1 i =1
∂β1 i =1

Cuya solución es: ˆ ˆ
β 0 = y − β1 x
 n y  n x 
 ∑ i  ∑ i 
n
 i =1  i =1 
∑ xi yi −
ˆ
β1 = i =1 n
2
 x
n
∑ i 
n
 
∑ x i − i =1
2
i =1 n
Ahora, el modelo de regresión lineal simple ajustado
(o recta estimada) es:
0 ˆ ˆ ˆ
y=β +β x
1

Con respecto al numerador y denominador de B1 suelen expresarse
como Sxy y Sxx respectivamente:

 n y  n x 
 ∑ i  ∑ i 
n
 i =1  i =1 
∑ xi yi − S xy
ˆ
β1 = i =1 n ˆ
β1 =
 xn
∑ i 
2
S xx
n
2  i =1 
∑ xi −
i =1 n
2
 x
n
∑ i 
n
2
S xx = ∑ x i −  i =1  = n (x − x )2
Puede demostrarse que: ∑ i
i =1 n i =1

y
 n y  n x 
 ∑ i  ∑ i  n
S xy = ∑ xi yi −  i =1  i =1  = ∑ ( xi − x ) yi
n

i =1 n i =1

Por otro lado puede demostrarse que los estimadores de β0 y β1 son
insesgados con varianzas:

1 x 2  σ2
V (β 0 ) = σ  +
ˆ 2 y V (β1 ) =
ˆ
n S xx 
respectivamente.
  S xx

Como σ2 (la varianza de los errores εi) es en general desconocida, para estimarla
definimos el residuo como: ei = yi − yi ˆ y la suma de cuadrados del error
como: n n
SS E = ∑ ei2 SS E = ∑ ( yi − yi )
2
ˆ
i =1 i =1
ˆ
que al sustituir yi también puede expresarse como: SS E = S yy − β1S xy
ˆ
n
donde: S yy = ∑ ( yi − y )
2

i =1
n
∑ ( yi − yi )
2
ˆ SS E
Entonces: E (MS E ) = σ σ 2 = MS E
2
Sea MS E = i =1
= ˆ
n−2 n−2

ˆ
Con lo anterior, las varianzas estimadas de β 0 ˆ
y β1
son respectivamente:
1 x 2  MS E
V (β 0 ) = MS E  +
ˆ ˆ y V (β1 ) =
ˆ ˆ
 n S xx 
 S xx
Además, si se cumplen los supuestos de que los εi se distribuyen
normalemte con media cero y varianza σ2, entonces, los estadísticos
ˆ
β0 − β0 ˆ
β1 − β1
T= y T=
1 x 2  MS E
MS E  + 
 n S xx  S xx

tienen cada uno distribución t de Student con n-2 grados de libertad.

Lo que permite efectuar pruebas de hipótes y calcular intervalos
de confianza sobre los parámetros de regresión β0 y β1 .


H 0 : β1 = 0
Un caso de particular interés es probar la hipótesis:
H1 : β1 ≠ 0

Ya que si la pendiente es igual cero, entonces puede significar o que la
variación de X no influye en la variación de Y, o que no hay regresión
lineal entre X y Y.

Por otro lado, si la pendiente es diferente de cero, entonces existirá algún
grado de asociación lineal entre las dos variables, es decir, la variabilidad
de X explica en cierta forma la variabiliad de Y (aunque no implica que no
pueda obtenerse un mejor ajuste con algún polinomio de mayor grado en
X).

Nota: si se utilizara en lugar de una recta, una curva con grado mayor a 1
en X pero grado 1 en los coeficientes de X, la regresión sigue siendo lineal,
ya que es lineal en los parámetros de regresión p.ej. Y=βo+β1x+β2x2
β β β


Estimación de intervalos de confianza en torno a la línea de regresión:
BANDAS DE CONFIANZA

Recta estimada
de regresión

Para un punto específico x0
y0 = E (Y x0 ) = β 0 + β1 x0
ˆ ˆ ˆ ˆ

x 1 xi x0 xn


Estimación de la respuesta media para un x0 específico:
µ y0 = y0 = E (Y x0 ) = β 0 + β1 x0
ˆˆ ˆ ˆ ˆ ˆ

 1 (xo − x )  2  1 (xo − x )2 
V ( y0 ) = σ  +
ˆ
2
 V ( y0 ) = MS E  +
ˆ ˆ 
n S xx 
 n S xx 
y0 − µ y0
ˆ
y0
ˆ tiene distribución normal, por lo que: ˆ
ˆ
V ( yo )
tiene distribución T de Student con n-2 grados de libertad, por lo
que los límites de confianza superior e inferior para la respuesta
media dado x0 están dados por: y0 ± tα / 2, n − 2 V ( yo )
ˆ ˆ

Graficando los limites de confianza superior e inferior de µ y0 para cada punto xi de
ˆ
X pueden dibujarse las bandas de confianza para la recta de regresión.

Puede observarse que la amplitud del intervalo de confianza es mínima cuando x0 = x
mientras que es mayor en los extremos de los valores observados de X.

Predicción de nuevas observaciones

Nótese que y0 es la respuesta media para los valores de xi seleccionados para
ˆ
encontrar la recta de regresión; sin embargo, frecuentemente es de interés
predecir la respuesta futura para un xa dado seleccionado posteriormente.

Sea Ya la observación futura en x = xa ., ; Ya es una variable aleatoria con
varianza σ2 y por otro lado, la varianza de ya = β 0 + β1 xa es Vˆ (ya ) = MSE 1 + 1 + (xaS− x ) 
2
ˆ ˆ ˆ ˆ  
n
 xx 



Regresion lineal

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a Regresion lineal

Similar a Regresion lineal (20)

Regresion lineal