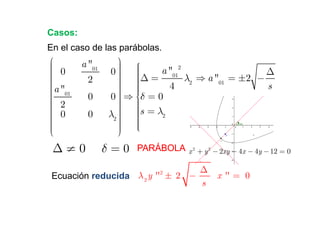
La cónica es el lugar geométrico de puntos que cumplen una ecuación de segundo grado. Puede representarse mediante una matriz asociada a su parte cuadrática, la cual puede diagonalizarse para obtener los ejes principales de la cónica. Existen diferentes tipos de cónicas como elipses, hipérbolas y rectas dependiendo de los signos de los autovalores y el término independiente.

2. Definición
Una cónica es el lugar geométrico de los puntos del
plano que verifican la igualdad :
a11x 2 + a22y 2 + a12xy + a01x + a02y + a00 = 0
Siendo aij ∈ ℝ y a11 , a 22 , a12 no todos nulos.

3. La expresión:
a11x 2 + a22y 2 + a12xy + a 01x + a 02y + a 00 = 0
Admite dos expresiones matriciales:
 
a12 
a
  
 11  x 
 x 


x y 
( )
a   
 y (
2   + a
01
a 02 )   + a 00 = 0

y 
 12    
 


2 a22 


 
Parte cuadrática Parte lineal

4. Que podemos escribirla de la forma:
t t
X Ac X + Al X + a 00 = 0
Donde:
X Es un punto del plano perteneciente a la cónica
Ac Matriz asociada a la parte cuadrática
Al Matriz asociada a la parte lineal
a 00 ∈ ℝ

5. Y esta otra:
 a 01 a 02 

a
 00 
 
 

 2 2  1

a
 a12   
 
 
(1 x y 
 )
 01 a11  x = 0
 
 
 2

2  

a 02 a12  
 y 

 a22 
 2
 2 

 
Que la escribimos:  
1
 
 
( )
1 x y A x  = 0
 
 
y 

 
 
A Matriz asociada a la cónica

6. Representación gráfica
Recuerda que:
El plano euclídeo E2 está formado por los puntos
de la forma P = O + x e1 + y e2 siendo:
O = (0, 0) origen de referencia
{e ,e }
1 2 base canónica de ℝ 2
OP vector de posición
(x , y ) coordenadas cartesianas de P que coinciden
con las coordenadas del vector de posición.

7. Cambio de bases ortonormales
{ }
B = e1 e2 {
B * = v1 v2 }
Figura 2
Figura 1
Figura 3

8. Matriz de paso de B*a B
x 
 x '

( )
 
OP = xe1 + ye2 = e1 e2  
y 
 
 
( ) 
OP = x ' v1 + y ' v2 = v1 v2  
y '
 
 

v = cos α e + sin α e cos α − sin α

1


1
v = − sin αe + cos αe
2
2
( ) (

⇒ v1 v2 = e1 e2  )
sin α cos α 







 1 2
La matriz de paso de B *a B es:
cos α −sin α x cos α −sin α x '
   

   
 ⇒  =   
P =      
sin α cos α  y sin α cos α y '
    
  
 

9. La expresión general de una cónica es:
a11x 2 + a22y 2 + a12xy + a01x + a02y + a00 = 0
t t
X Ac X + Al X + a 00 = 0
La parte cuadrática es una matriz real y simétrica y podemos
{ }
diagonalizarla por semejanza ortogonal con v1 , v2 una base
ortonormal de vectores propios y λ1 , λ2 los autovalores.
Haciendo un cambio de bases ortonormales obtenemos:
t
X = PX ' ⇒ (PX ') A (PX ') + At (PX ') +a00 = 0
c l
Luego:
t t
( ( c
t
) l
t
l ( )
X ') P AP X '+ A PX '+a00 = 0 ⇒ (X ') DX '+ AtP X '+a00 = 0

10. siendo:
cos α −sin α
 λ 0 

   
P =
sin α cos α  D = 1
0 λ 

 

  
 2

Quedando la cónica reducida a la expresión:
λ1x '2 + λ2y '2 + a '01 x '+ a '02 y '+ a00 = 0
Sin término x 'y '
El orden de los autovalores es importante y tiene que
ver con realizar el giro de forma adecuada, ya que los
vectores propios asociados se corresponden con el
eje principal y secundario de la cónica.

11. En la expresión:
λ1x '2 + λ2y '2 + a '01 x '+ a '02 y '+ a00 = 0
Si λ1 ≠ 0 y λ2 ≠ 0 podemos completar cuadrados:
2
 a '01  a '012

2 x '+
λ1x ' + a '01 x ' = λ1   −
 


 2λ1   4λ12
2
  a' 2
2 y '+ a '02  − 02
λ2y ' + a '02 y ' = λ2  
 


 2λ2   4λ22

12. Y haciendo la traslación:
a '01 a '02
x ' = x ''− y ' = y ''−
2λ1 2λ2
Obtenemos: λ1x ''2 + λ2y ''2 + a ''00 = 0
Llamada ecuación reducida de la cónica.
Casos:
signo (λ1 ) = signo (λ2 ) ≠ signo (a ''00 ) ELIPSE REAL
signo (λ1 ) = signo (λ2 ) = signo (a ''00 ) ELIPSE IMAGINARIA
signo (λ1 ) = signo (λ2 ) y a ''00 = 0 PAR de RECTAS SECANTES
IMAGINARIAS

13. signo (λ1 ) ≠ signo (λ2 ) y signo (a ''00 ) = signo (λ2 )
HIPÉRBOLA DE EJE REAL OX
signo (λ1 ) ≠ signo (λ2 ) y signo (a ''00 ) = signo (λ1 )
HIPÉRBOLA DE EJE REAL OY
signo (λ1 ) ≠ signo (λ2 ) y a ''00 = 0
PAR de RECTAS SECANTES REALES

14. Si λ1 = 0, λ2 ≠ 0 , a 01 ≠ 0 solo podemos completar la y´
λ2y '2 + a '01 x '+ a '02 y '+ a00 = 0
2
 a '02  a '022

2 y '+
λ2y ' + a '02 y ' = λ2   −
 


 2λ2   4λ2 2
Y haciendo la traslación:
2
a 00 a '02 a '02
x ' = x ''− + y ' = y ''−
a '01 4λ22a '01 2λ2
2
obtenemos: λ2y '' + a ''01 x '' = 0 PARÁBOLA

15. Si λ1 = 0, λ2 ≠ 0 , a 01 = 0 solo aparece la y´
λ2y '2 + a '02 y '+ a00 = 0
2
 a '02  a '022

2 y '+
λ2y ' + a '02 y ' = λ2   −
 


 2λ2   4λ2 2
a '02
Y haciendo la traslación: y ' = y ''−
2λ2
2
obtenemos: λ2y '' + a ''00 = 0
Si signo (a ''00 ) = signo (λ2 ) PAR DE RECTAS PARALELAS IMAGINARIAS
Si signo (a ''00 ) ≠ signo (λ2 ) PAR DE RECTAS PARALELAS REALES

16. INVARIANTES de una CÓNICA
Son aquellas expresiones formadas con los coeficientes
de la ecuación que no varían al reducir la cónica.
Son invariantes:
a 01 a 02 a12
a 00 a11
2 2 2
a 01 a12 δ=
∆= a11 a12
a22
2 2 2
a 02 a12
a22
2 2 s = Tr (Ac ) = a11 + a22

17. INVARIANTES de una CÓNICA
Utilizando los valores propios, junto con los invariantes,
podemos obtener la forma reducida de manera más
cómoda.
En el caso de elipses, hipérbolas y rectas secantes, la
matriz de la cónica reducida es:


a ''  ∆ = a '' λ λ ⇒ a '' = ∆
 00 0 0 
  00 1 2 00

   δ
 0
 λ1 0  ⇒ δ = λ1λ2
 
 
  

 0
 0 λ2  s = λ1 + λ2
 
 



18. Casos:
signo (λ1 ) = signo (λ2 ) ≠ signo (a ''00 )
∆≠0 δ>0 ∆⋅s < 0
ELIPSE REAL
2 2 ∆
Ecuación reducida λ1x '' + λ2y '' + = 0
δ
5x 2 + 8y 2 − 4xy + 10x − 4y − 31 = 0

19. Casos:
signo (λ1 ) = signo (λ2 ) = signo (a ''00 )
∆≠0 δ>0 ∆⋅s > 0
ELIPSE IMAGINARIA
2 2 ∆
Ecuación reducida λ1x '' + λ2y '' + = 0
δ
signo (λ1 ) = signo (λ2 ) a ''00 = 0
∆=0 δ>0
PAR DE RECTAS SECANTES IMAGINARIAS
2 2
Ecuación reducida λ1x '' + λ2y '' = 0

20. Casos:
signo (λ1 ) ≠ signo (λ2 ) a 00 ≠ 0
∆≠0 δ<0
HIPÉRBOLA
2 2 ∆
Ecuación reducida λ1x '' + λ2y '' + = 0
δ
x 2 + y 2 + 10xy − 6x − 6y + 2 = 0

21. Casos:
signo (λ1 ) ≠ signo (λ2 ) a 00 = 0
∆=0 δ<0
PAR DE RECTAS SECANTES REALES
2 2
Ecuación reducida λ1x '' + λ2y '' = 0
2x 2 − y 2 − xy + 3y − 2 = 0

22. Casos:
En el caso de las parábolas.
 a ''01 
 

 0  
0  a ''012 ∆

 2  ∆ = λ2 ⇒ a ''01 = ±2 −
  
 
a ''
  
  4 s
 01
 0 
0  ⇒ δ = 0
  
 2
 0
 
 s = λ

 0 λ2  
 
 2

  
 

  

∆≠0 δ=0 PARÁBOLA x 2 + y 2 − 2xy − 4x − 4y − 12 = 0
2 ∆
Ecuación reducida λ 2 y '' ± 2 − x '' = 0
s

23. Casos:
En el caso de las rectas paralelas o coincidentes
a '' 0  
 
0  ∆ = 0

 00 
  
 ⇒ δ = 0
 0
 0 0  
  
 0

 0 λ2  s = λ2
 
 
∆=0 δ=0 RECTAS PARALELAS o
COINCIDENTES
Con los invariantes que tenemos no podemos calcular la
ecuación reducida, para ello la escribimos como una
ecuación de segundo grado en y o en x, resolviéndola.

24. Clasificación
Cónica no degenerada

 
 
∆ ⋅ s > 0 Elipse imaginaria

 
δ > 0 
  

δ ≠ 0 
 
∆ ⋅ s < 0 Elipse real
∆ ≠ 0 
 δ < 0 Hiperbola


 

δ = 0 Parabola



Cónica degenerada

 δ > 0 Par de rectas secantes imaginarias


δ ≠ 0 
 
∆ = 0 δ < 0 Par de rectas secantes reales

 
δ = 0 Par de rectas paralelas o coincidentes




25. Cálculo de los elementos de una cónica
Tomando
f (x ) = a11x 2 + a22y 2 + a12xy + a01x + a02y + a00
Centro (α, β )
Las cónicas que tienen centro son aquellas donde δ≠0
Se obtiene resolviendo el siguiente sistema:
 ∂f


 (α, β ) = 0
 ∂x

 ∂f

 (α, β ) = 0

 ∂y



26. Cálculo de los elementos de una cónica
Ejes
Son las rectas que pasan por el centro y tienen la dirección
de los vectores propios.
En una elipse, el autovalor que determina el autovector de
dirección el eje real debe ser el menor en valor absoluto.
En una hipérbola, el autovalor que determina el autovector
de dirección el eje real, debe ser el de distinto signo que
∆
a ''00 =
δ

27. Cálculo de los elementos de una cónica
Vértice de la parábola
Para calcular el vértice de una parábola, resolveremos el
sistema que se obtiene al imponer a las coordenadas del
mismo que cumplan la ecuación de la parábola y que la
pendiente de la tangente en ese punto, sea perpendicular
a la dirección del autovector asociado al autovalor no nulo.
Eje de la parábola
Recta que pasa por el vértice y tiene la dirección del
autovector asociado al autovalor nulo.