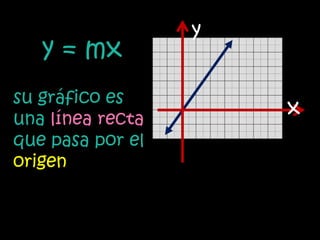
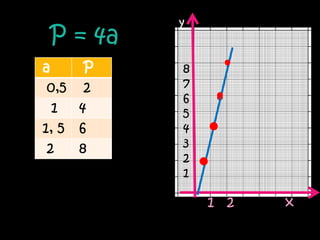
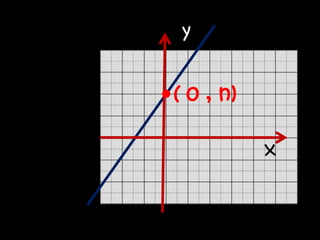
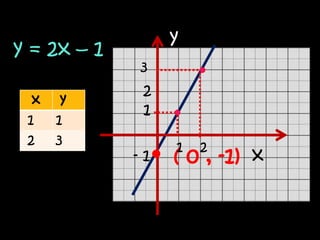
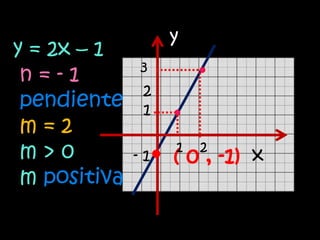
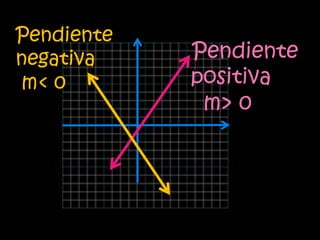
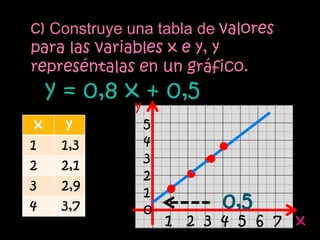
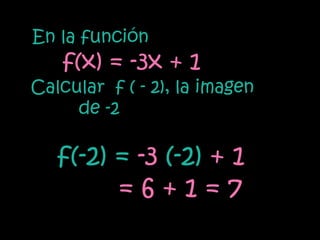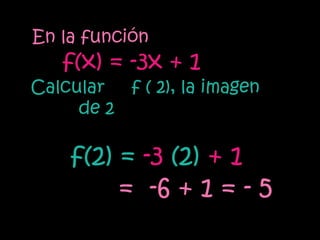La función lineal se expresa como y=mx, donde m es la pendiente y x e y son las variables independiente y dependiente. La función afín se expresa como y=mx+n, donde m es la pendiente, n es la ordenada al origen y x e y son las variables. Ambas funciones relacionan variables a través de ecuaciones o gráficas de rectas.

1. FUNCIÓN LINEAL
y = mx
FUNCIÓN AFÍN
y = mx + n
María Pizarro Aragonés

2. Una función lineal es
aquella cuya expresión
matemática viene dada por
y = mx
x e y son variables y m una
constante que se llama
pendiente

3. y = mx
variable variable
dependiente independiente

4. y
y = mx
su gráfico es
una línea recta
x
que pasa por el
origen

5. Perímetro de un cuadrado
de lado a
P= 4a
P variable dependiente
a variable independiente

6. y
P = 4a
a P 8
0,5 2 7
6
1 4 5
1, 5 6 4
2 8 3
2
1
1 2 x

7. Una función afín es
aquella cuya expresión
matemática viene
dada por:
Como
ecuación
f(x) = mx + n como
función

8. donde x e y son
variables, m una
constante que se
denomina pendiente

9. otra constante n
denominada ordenada en el
origen o coeficiente de
posición.

10. . Su gráfica es una
recta que corta al
eje de ordenadas en
(0, n) .

11. y
( 0 , n)
x

12. Representar gráficamente la
función y = 2x – 1
y = 2•1 – 1 = 2-1= 1
y = 2•2 – 1 = 4-1= 3
x y
1 1
2 3

13. y
y = 2x – 1
3
2
x y
1
1 1
2 3 1 2
-1 ( 0 , -1) x

14. y
y = 2x – 1
3
n=-1
2
pendiente 1
m=2
m>0 -1
1 2
( 0 , -1) x
m positiva

15. Pendiente
negativa Pendiente
m< 0 positiva
m> 0

16. Representar gráficamente
y=-x+3
m = -1 n=3
(0, 3)
x y
1 2
2 1
y=-1+3=2
y=-2+3=1

17. En la función
f(x) = -3x + 1
Calcular f ( - 2), la imagen
de -2
f(-2) = -3 (-2) + 1
=6+1=7

18. En la función
f(x) = -3x + 1
Calcular f ( 2), la imagen
de 2
f(2) = -3 (2) + 1
= -6 + 1 = - 5

19. Determina la pendiente
y el punto donde corta al
eje y la función:
y=-x–3
m=-1
Corta al eje Y en el punto
(0 , - 3)

20. El costo inicial para fabricar
sopaipillas incluye un costo fijo
de $5.000 más un costo de $80 por
cada unidad. Determinar la funcion
expresa el costo total (C) , en
pesos, para fabricar x sopaipillas?

21. Costo fijo $5.000.
Cada sopaipilla
cuesta $80.
Costo de 100 sopaipillas
5.000 + 100•80 =
5.000 + 8.000 = $13.000

22. costo fijo de $5.000 más un costo
de $80 por cada unidad.
Determinar la función que expresa
el costo total (C) , en pesos, para
fabricar x sopaipillas?
C = 5.000 + 80x ó
C = 80x + 5.000

23. C = 80x + 5.000
es una función afín.
¿ Cuál es el costo total para
fabricar 600 sopaipillas?
C = 80•600 + 5.000
C = 48.000 + 5.000 =
$53.000

24. René va a comprar parafina con un
bidón.
1 litro de parafina pesa 0,8 kg.
El bidón vacío pesa medio kilo.(0,5 kg)
pesa 0,5 kg

25. 1 litro de parafina pesa 0,8 kg.
Si René compra 8 litros de parafina,
¿cuántos kilos tiene que cargar de vuelta
a su casa?
0,8•8 = 6,4 kg peso de 8 litros
Total 6,4 + 0,5
= 6,9 kg
pesa 0,5 kg

26. 1 litro de parafina pesa 0,8 kg. El
bidón vacío pesa medio kilo.
b) El peso total del bidón con
parafina depende de la cantidad de
litros comprados.
Si x representa cuántos litros de
parafina compró René e y el peso
del bidón con parafina,

27. ¿cuál es la fórmula que relaciona las
variables x e y?
y = 0,8 x + 0,5

28. ¿cuál es la fórmula que relaciona las
variables x e y?
y = 0,8 x + 0,5
Peso de un litro
peso del bidón

29. c) Construye una tabla de valores
para las variables x e y, y
represéntalas en un gráfico.
y = 0,8 x + 0,5
y
x y 5
1 1,3 4
2 2,1 3
2
3 2,9 1
4 3,7 0 0,5
1 2 3 4 5 6 7 x

30. FIN
Bibliografía : Wikipedia
EducarChile