teoria para optimizar y calcular valores máximo y mínimo de una función multivariable.

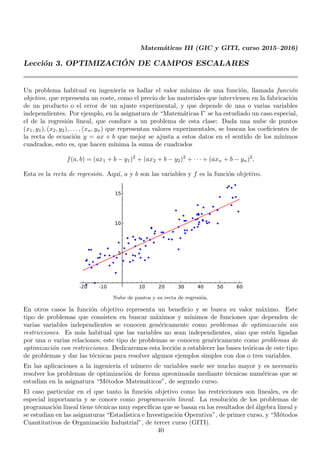
1. Matem´aticas III (GIC y GITI, curso 2015–2016)
Lecci´on 3. OPTIMIZACI ´ON DE CAMPOS ESCALARES
Un problema habitual en ingenier´ıa es hallar el valor m´ınimo de una funci´on, llamada funci´on
objetivo, que representa un coste, como el precio de los materiales que intervienen en la fabricaci´on
de un producto o el error de un ajuste experimental, y que depende de una o varias variables
independientes. Por ejemplo, en la asignatura de “Matem´aticas I” se ha estudiado un caso especial,
el de la regresi´on lineal, que conduce a un problema de esta clase: Dada una nube de puntos
(x1, y1), (x2, y2), . . . , (xn, yn) que representan valores experimentales, se buscan los coeficientes de
la recta de ecuaci´on y = ax + b que mejor se ajusta a estos datos en el sentido de los m´ınimos
cuadrados, esto es, que hacen m´ınima la suma de cuadrados
f(a, b) = (ax1 + b − y1)2
+ (ax2 + b − y2)2
+ · · · + (axn + b − yn)2
.
Esta es la recta de regresi´on. Aqu´ı, a y b son las variables y f es la funci´on objetivo.
Nube de puntos y su recta de regresi´on.
En otros casos la funci´on objetivo representa un beneficio y se busca su valor m´aximo. Este
tipo de problemas que consisten en buscar m´aximos y m´ınimos de funciones que dependen de
varias variables independientes se conocen gen´ericamente como problemas de optimizaci´on sin
restricciones. Es m´as habitual que las variables no sean independientes, sino que est´en ligadas
por una o varias relaciones; este tipo de problemas se conocen gen´ericamente como problemas de
optimizaci´on con restricciones. Dedicaremos esta lecci´on a establecer las bases te´oricas de este tipo
de problemas y dar las t´ecnicas para resolver algunos ejemplos simples con dos o tres variables.
En las aplicaciones a la ingenier´ıa el n´umero de variables suele ser mucho mayor y es necesario
resolver los problemas de optimizaci´on de forma aproximada mediante t´ecnicas num´ericas que se
estudian en la asignatura “M´etodos Matem´aticos”, de segundo curso.
El caso particular en el que tanto la funci´on objetivo como las restricciones son lineales, es de
especial importancia y se conoce como programaci´on lineal. La resoluci´on de los problemas de
programaci´on lineal tiene t´ecnicas muy espec´ıficas que se basan en los resultados del ´algebra lineal y
se estudian en las asignaturas “Estad´ıstica e Investigaci´on Operativa”, de primer curso, y “M´etodos
Cuantitativos de Organizaci´on Industrial”, de tercer curso (GITI).
40

2. 3. Optimizaci´on de campos escalares 41
Si recordamos el caso de las funciones de una variable, la determinaci´on de los m´aximos y los
m´ınimos absolutos de una funci´on en un intervalo se lleva a cabo usando las derivadas. En el
bachillerato se ense˜na que los puntos candidatos a que en ellos se alcance el m´aximo o el m´ınimo
absoluto de una funci´on son los puntos en los que la derivada vale cero, los extremos del intervalo
y los puntos donde la derivada no existe; adem´as, cuando la derivada primera es cero, entonces que
la derivada segunda sea positiva o negativa nos dice, respectivamente, si estamos ante un m´ınimo
relativo o un m´aximo relativo. Veremos que cuando la funci´on objetivo depende de dos o m´as
variables, la diferenciabilidad tambi´en es la herramienta que permite resolver los problemas de
optimizaci´on.
Dedicaremos la primera secci´on a la optimizaci´on sin restricciones, donde analizaremos las nociones
de extremo absoluto, extremo relativo y punto de silla. En el caso de dos variables se intuye que en
un m´aximo, o en un m´ınimo, el plano tangente a la gr´afica del campo escalar debe ser horizontal
y, por tanto, las derivadas parciales deben ser nulas; sin embargo, no est´a claro a priori el papel
que deben tener las derivadas parciales segundas para dilucidar si se trata de m´aximos o m´ınimos.
Esto lo estudiaremos tambi´en en esta secci´on, viendo que la herramienta esencial para determinar
c´omo es dicho papel es la clasificaci´on de la forma cuadr´atica asociada a la matriz hessiana.
El estudio de los problemas de optimizaci´on con restricciones lo empezamos en la segunda secci´on,
en la que abordaremos el problema de calcular los m´aximos y minimos relativos de una funci´on de
dos o tres variables sobre una curva dada de forma impl´ıcita por una igualdad, en el plano, o dos
igualdades, en el espacio tridimensional. Tambi´en analizaremos el caso en el que la restricci´on es
una superficie dada de forma impl´ıcita.
Finalmente, en la tercera secci´on, analizaremos la existencia de los m´aximos y m´ınimos absolutos
de una funci´on escalar de dos o tres variables con restricciones generales y el procedimiento para
calcularlos.
Enunciaremos los resultados para funciones de tres variables aunque la mayor´ıa son v´alidos para
funciones de m´as variables. Como venimos haciendo, usaremos el caso bidimensional, en el que
basta con suprimir la coordenada z (y cambiar “esfera” por “c´ırculo” en lo que sigue), para poner
ejemplos y dar las interpretaciones geom´etricas.
1. OPTIMIZACI ´ON SIN RESTRICCIONES
Extremos absolutos. En un problema de optimizaci´on sin restricciones tenemos una funci´on
f, llamada funci´on objetivo, definida en un conjunto U, que generalmente ser´a todo el espacio, y
queremos calcular los puntos, si es que existen, en los que f alcanza su valor m´aximo y su valor
m´ınimo; es decir, buscamos los puntos Pm´ın, Pm´ax ∈ U tales que
f(Pm´ın) ≤ f(P) ≤ f(Pm´ax) para todo P ∈ U.
Los valores m´aximo y m´ınimo de f y, por abuso de lenguaje, los puntos en los que se alcanzan
dichos valores, se llaman extremos absolutos, o globales, de f en U.
Como ejemplo de partida, antes de abordar los problemas de optimizaci´on sin restricciones en el
caso general, nos detenemos en el caso particular de las formas cuadr´aticas que has estudiado en
“Matem´aticas I”. La raz´on es doble: por un lado, porque es un caso simple en el que podemos ir
se˜nalando las principales cuestiones con las que nos encontraremos y, por otro lado, porque ser´a
esencial para determinar el car´acter de los puntos cr´ıticos, los puntos en los que se anulan las
derivadas parciales de la funci´on objetivo. Empezamos recordando c´omo se clasifican las formas
cuadr´aticas en t´erminos del signo que pueden tomar sus autovalores y viendo c´omo se relaciona
esto con sus extremos absolutos.

3. 42 Matem´aticas III (GIC y GITI, 2015–2016)
Forma cuadr´atica generada por una matriz sim´etrica. Sea A = [aij] una matriz cuadrada,
real y sim´etrica de orden 3, entonces el campo escalar definido en R3
por
ψ(x, y, z) = [x, y, z]


a11 a12 a13
a21 a22 a23
a31 a32 a33




x
y
z


se llama forma cuadr´atica generada por A y se puede escribir de forma desarrollada como
ψ(x, y, z) = a11x2
+ a22y2
+ a33z2
+ 2a12xy + 2a13xz + 2a23yz.
Clasificaci´on de las formas cuadr´aticas. Se dice que una forma cuadr´atica no nula ψ o, por
extensi´on, la matriz real sim´etrica A que la genera, es:
(1) Definida positiva si ψ(x, y, z) > 0 para todo (x, y, z) ̸= (0, 0, 0) o, equivalentemente, si todos
los autovalores de A son positivos o, equivalentemente, si el origen es el ´unico punto en el que se
alcanza el m´ınimo absoluto.
En dimensi´on dos, la gr´afica de una forma cuadr´atica definida positiva es un paraboloide el´ıptico
con su v´ertice en el origen que se abre hacia arriba, por lo que no existe el m´aximo absoluto, ya
que los valores de ψ tienden a infinito cuando el punto (x, y) tiende a infinito.
Gr´afica de una forma cuadr´atica con m´ınimo absoluto.
(2) Semidefinida positiva si ψ(x, y, z) ≥ 0 para todo (x, y, z) y hay puntos (x, y, z) ̸= (0, 0, 0) tales
que ψ(x, y, z) = 0 o, equivalentemente, si 0 es un autovalor y los dem´as autovalores λ de A cumplen
λ ≥ 0 o, equivalentemente, si hay una recta o un plano de m´ınimos absolutos que pasa por el origen.
(3) Definida negativa si ψ(x, y, z) < 0 para todo (x, y, z) ̸= (0, 0, 0) o, equivalentemente, si todos
los autovalores de A son negativos o, equivalentemente, si el origen es el ´unico punto en el que se
alcanza un m´aximo absoluto.
En dimensi´on dos, la gr´afica de una forma cuadr´atica definida negativa es un paraboloide el´ıptico
con su v´ertice en el origen que se abre hacia abajo, por lo que no existe el m´ınimo absoluto, ya que
los valores de ψ tienden a −∞ cuando el punto (x, y) tiende a infinito.
Gr´afica de una forma cuadr´atica con m´aximo absoluto.

4. 3. Optimizaci´on de campos escalares 43
(4) Semidefinida negativa si ψ(x, y, z) ≤ 0 para todo (x, y, z) y hay puntos (x, y, z) ̸= (0, 0, 0)
tales que ψ(x, y, z) = 0 o, equivalentemente, si 0 es un autovalor y los dem´as autovalores λ de A
cumplen λ ≤ 0 o, equivalentemente, si hay una recta o un plano de m´aximos absolutos que pasa
por el origen.
(5) Indefinida si no es definida ni semidefinida; o sea, si existen vectores (x, y, z) tales que
ψ(x, y, z) < 0 y existen vectores (x, y, z) tales que ψ(x, y, z) > 0 o, equivalentemente, si A tie-
ne alg´un autovalor positivo y alg´un autovalor negativo o, equivalentemente, si no tiene m´aximos
ni m´ınimos absolutos.
Gr´afica de una forma cuadr´atica sin m´ınimo ni m´aximo y silla de montar.
Desde el punto de vista geom´etrico, la gr´afica de una forma cuadr´atica indefinida en dimensi´on
dos es un paraboloide hiperb´olico, con centro en el origen, que se abre hacia arriba a lo largo de la
direcci´on del autovector asociado el autovalor positivo y hacia abajo a lo largo de la direcci´on del
autovector asociado al autovector negativo. Debido al parecido de esta gr´afica con el de una silla
de montar a caballo, se dice que el origen es un punto de silla.
M´as adelante en la secci´on aplicaremos esta clasificaci´on a la matriz hessiana de un campo escalar
para determinar cu´ando un punto en el que las derivadas parciales son cero es un m´ınimo relativo
o un m´aximo relativo.
Determinar los autovalores suele ser un trabajo complicado; sin embargo, lo ´unico que necesitamos
conocer son los signos de los autovalores y para ello hay criterios relativamente simples de aplicar
en el caso bidimensional.
Criterios de clasificaci´on para una matriz sim´etrica 2×2. Sea A una matriz real y sim´etrica
de orden 2. Sean t = a11 +a22 su traza y d = a11a22 −a21a12 su determinante. Entonces se cumple
lo siguiente:
(1) Si d > 0 y t > 0, entonces A es definida positiva.
(2) Si d > 0 y t < 0, entonces A es definida negativa.
(3) Si d < 0, entonces A es indefinida.
(4) Si d = 0 y t > 0, entonces A es semidefinida positiva.
(5) Si d = 0 y t < 0, entonces A es semidefinida negativa.
Algunas consideraciones sobre los problemas de optimizaci´on sin restricciones. Como
acabamos de ver con diversos ejemplos de formas cuadr´aticas, los problemas de optimizaci´on sin
restricciones pueden no tener soluci´on. En algunos casos puede deducirse que debe existir el m´aximo
absoluto o el m´ınimo absoluto estudiando el comportamiento de la funci´on objetivo cuando (x, y)
tiende a infinito, pero eso no siempre es f´acil de hacer.
A la hora de abordar un problema, una idea central es restringir la b´usqueda de los extremos
absolutos a un conjunto, deseablemente finito, de puntos que verifiquen alguna condici´on especial.
La m´as com´un, que ya se conoce en el caso de las funciones de una variable, es la de extremo

5. 44 Matem´aticas III (GIC y GITI, 2015–2016)
relativo: puntos donde la funci´on alcanza su valor m´aximo o su valor m´ınimo entre los puntos
suficientemente cercanos. Como ya hemos comentado antes y hemos visto en el caso de las formas
cuadr´aticas de dos variables, la intuici´on geom´etrica nos dice que si una funci´on definida en todos
los puntos del plano alcanza un extremo relativo en un punto, entonces el plano tangente a su
gr´afica en dicho punto debe ser horizontal, lo que nos dar´ıa una condici´on pr´actica para restringir
la b´usqueda de extremos absolutos. Vamos ahora a fijar todas estas ideas con precisi´on.
Extremos relativos. Se dice que f : U → R tiene un m´aximo relativo o m´aximo local en un
punto P0 ∈ U si existe una esfera D centrada en P0 y contenida en U tal que f(P0) ≥ f(P) para
todo P ∈ D.
Se dice que f tiene un m´ınimo relativo o m´ınimo local en un punto P0 ∈ U si existe una esfera D
centrada en P0 y contenida en U tal que f(P0) ≤ f(P) para todo P ∈ D.
Los m´aximos relativos y m´ınimos relativos de f se llaman gen´ericamente extremos relativos, o
locales, de f.
La gr´afica de una funci´on con dos m´aximos relativos; s´olo uno de ellos es absoluto.
Criterio de las derivadas parciales nulas para los extremos relativos o condici´on nece-
saria de extremo relativo. Si la funci´on objetivo f y tiene un extremo relativo en un punto P0
y es diferenciable en dicho punto, entonces Df(P0) = ⃗0.
En el caso de que f dependa de dos variables, tenemos
∂f
∂x
(P0) = 0 y
∂f
∂y
(P0) = 0, es decir,
efectivamente, el plano tangente a la gr´afica de f es horizontal.
Para tres variables, tenemos
∂f
∂x
(P0) = 0,
∂f
∂y
(P0) = 0 y
∂f
∂z
(P0) = 0.
Ejemplo. En el ejemplo de la recta de regresi´on, dados los puntos (x1, y1), (x2, y2), . . . , (xn, yn) se
buscan los coeficientes de la recta de ecuaci´on y = ax + b que hacen m´ınima la suma de cuadrados
f(a, b) =
n∑
k=1
(axk + b − yk)2
. Imponiendo
∂f
∂a
=
∂f
∂b
= 0 obtenemos que los coeficientes ´optimos
a, b son las soluciones del sistema de ecuaciones
( n∑
k=1
x2
k
)
a +
( n∑
k=1
xk
)
b =
n∑
k=1
xkyk
( n∑
k=1
xk
)
a + nb =
n∑
k=1
yk
que son, como se ha visto en “Matem´aticas I”, las ecuaciones normales de Gauss del sistema
sobredeterminado
[
x1 x2 . . . xn
1 1 . . . 1
]T [
a
b
]
= [ y1 y2 . . . yn ]
T
.

6. 3. Optimizaci´on de campos escalares 45
Punto cr´ıtico. Se dice que un punto P0 ∈ U es un punto cr´ıtico o punto estacionario de la
funci´on objetivo f cuando Df(P0) = ⃗0.
Incluso en el caso bidimensional, la resoluci´on del sistema de ecuaciones
∂f
∂x
= 0,
∂f
∂y
= 0 pue-
de ser complicada o, en algunos casos, imposible de hacer a mano. En estos casos, hay que
emplear m´etodos num´ericos para obtener soluciones aproximadas que se estudiar´an en la asignatura
“M´etodos Matem´aticos” de segundo curso.
Puntos de silla. El teorema anterior nos dice que cualquier extremo relativo es un punto cr´ıtico.
Como ya hemos visto con las formas cuadr´aticas y es conocido del caso de una variable, el rec´ıproco
es falso en general. As´ı, hemos probado que la funci´on objetivo f(x, y) = x2
− y2
tiene un punto
cr´ıtico en (0, 0) y que, sin embargo, dicho punto no es un m´aximo relativo ni un m´ınimo relativo.
Los puntos cr´ıticos de una funci´on que no son extremos relativos de la misma se llaman puntos de
silla. Tan cerca como queramos de un punto de silla encontramos puntos en los que la funci´on vale
m´as y puntos en los que la funci´on vale menos que en el propio punto cr´ıtico.
Clasificaci´on de los puntos cr´ıticos. ¿C´omo podemos saber si un punto cr´ıtico es un m´aximo
relativo, un m´ınimo relativo o un punto de silla? Geom´etricamente, para funciones de dos variables,
el plano tangente a la gr´afica en los puntos cr´ıticos es un plano horizontal. En los m´aximos y
m´ınimos locales, cerca del punto el plano deja a un lado la superficie; en los puntos de silla, la
atraviesa. La geometr´ıa de los puntos de silla se parece a la de los puertos de monta˜na: los puntos
m´as bajos hasta los que hay que subir para atravesar una sierra, por ello, a los puntos de silla
tambi´en se les llama puertos.
Como regla general, pero no siempre, si observamos las curvas de nivel, en torno a los m´aximos
y m´ınimos locales, las curvas de nivel aparecen como curvas cerradas. En los m´ınimos las curvas
se alejan del punto conforme el nivel crece; en los m´aximos se acercan al punto conforme el nivel
crece. En ambos casos, las curvas de nivel degeneran cuando nos acercamos al punto cr´ıtico; lo
que, recordando el teorema de la funci´on impl´ıcita, nos dice que al ser ambas derivadas parciales
nulas, no podemos aplicar ese teorema para despejar una variable en funci´on de la otra en la curva
de nivel, de hecho la curva de nivel en un m´aximo o un m´ınimo local se reduce a un punto; no es
propiamente una curva.
Un punto de silla o puerto. M´aximos (A), m´ınimos (B) y puntos de silla (C).
En los puntos de silla las curvas de nivel aparentan acercarse y alejarse del punto sin llegar a
rodearlo y suelen aparecer dos curvas del mismo nivel que pasan justamente por el punto; en este
caso, no es posible aplicar el teorema de la funci´on impl´ıcita para despejar una variable en funci´on
de la otra, de hecho la ecuaci´on impl´ıcita corresponde a dos curvas de nivel, no una sola.
Anal´ıticamente, para las funciones de una variable la determinaci´on de si un punto cr´ıtico es un
m´aximo relativo o un m´ınimo relativo se hace analizando el signo de la derivada segunda; aqu´ı

7. 46 Matem´aticas III (GIC y GITI, 2015–2016)
se hace algo parecido aunque m´as complicado: utilizamos el teorema de Taylor y clasificamos la
forma cuadr´atica generada por la matriz hessiana. Para ello, observemos que si (x0, y0) es un
punto cr´ıtico, de manera que Df(x0, y0) = ⃗0 entonces el Teorema de Taylor nos dice que para
(x, y) suficientemente cerca de (x0, y0) se tiene
f(x, y) ≈ f(x0, y0) +
1
2
[
x − x0, y − y0
]
D2
f(x0, y0)
[
x − x0
y − y0,
]
Por tanto, que f(x, y) sea mayor o menor que f(x0, y0) depende del signo de la forma cuadr´atica
generada por la matriz hessiana D2
f(x0, y0).
El test de las derivadas segundas o condici´on suficiente de extremo relativo. Supongamos
que la funci´on objetivo es de clase C2
(U) y que P0 es un punto cr´ıtico de f; esto es, tal que
Df(P0) = ⃗0. Entonces, seg´un sea la forma cuadr´atica generada por la matriz hessiana D2
f(P0),
se tiene lo siguiente:
(1) Si D2
f(P0) es definida positiva, entonces f tiene en P0 un m´ınimo relativo.
(2) Si D2
f(P0) es definida negativa, entonces f tiene en P0 un m´aximo relativo.
(3) Si D2
f(P0) es indefinida, entonces f tiene en P0 un punto de silla.
(4) Si D2
f(P0) es semidefinida, entonces las derivadas segundas no dan informaci´on.
Ejemplos. (1) La funci´on f(x, y) = x2
+ ky2
tiene un punto cr´ıtico en (0, 0). En dicho punto, la
matriz hessiana es
(
2 0
0 2k
)
. En funci´on del signo de k obtenemos que:
(1) Si k > 0, entonces la matriz es definida positiva y por tanto (0, 0) es un m´ınimo relativo.
(2) Si k < 0, entonces la matriz es indefinida y por tanto (0, 0) es un punto de silla.
(3) Si k = 0, entonces la matriz es semidefinida, por lo que el m´etodo no da informaci´on.
Si observamos la funci´on en este caso vemos que f(x, y) = x2
≥ 0 = f(0, 0), para todo
(x, y) ∈ R2
. Por tanto (0, 0) es un m´ınimo relativo de f.
(2) La funci´on f(x, y) = x2
+ ky2
− y3
tiene un punto cr´ıtico en (0, 0). En dicho punto, la matriz
hessiana es la misma que en el ejemplo anterior
(
2 0
0 2k
)
. Sin embargo, en el caso en que la forma
cuadr´atica es indefinida, el tipo de punto cr´ıtico es distinto. En efecto, en funci´on del signo de k
obtenemos que:
(1) Si k > 0, entonces la matriz es definida positiva y por tanto (0, 0) es un m´ınimo relativo.
(2) Si k < 0, entonces la matriz es indefinida y por tanto (0, 0) es un punto de silla.
(3) Si k = 0, entonces la matriz es semidefinida, por lo que el m´etodo no da informaci´on. En
este caso vemos que f(x, y) = x2
− y3
y, usando el mismo razonamiento que vimos antes
para x2
− y2
, es f´acil deducir que (0, 0) es un punto de silla de f.
EJERCICIOS DE LA SECCI´ON 1
Ejercicio 1. Halla y clasifica los puntos cr´ıticos de los siguientes campos escalares (utiliza alguna
de las p´aginas web que se indican al final del gui´on para dibujar las gr´aficas y las curvas de nivel
del campo).
(1) f(x, y) = x4
− 2x2
y − 6x2
+ 4y2
(2) f(x, y) = x3
+ 3xy2
− 15x − 12y
(3) f(x, y) = 12x2
+ 12y2
− x3
y3
+ 5 (4) f(x, y) = (x2
+ y2
)ex2
−y2
(5) f(x, y) = x2
y + xy2
+ x + y (6) f(x, y) = (1 − x2
− y2
)2
(7) f(x, y) = x2
y2
(8) f(x, y) = cos(x) cos(y)
(9) f(x, y) = x3
+ y3
− 3xy (10) f(x, y) = x sen(y)

8. 3. Optimizaci´on de campos escalares 47
Ejercicio 2. El origen es un punto cr´ıtico del campo escalar definido por f(x, y) = x2
+y2
+αxy.
Determina qu´e tipo de punto cr´ıtico es seg´un los valores de α.
Ejercicio 3. Prueba que la ecuaci´on z cos(z) + xy = 0 define impl´ıcitamente z como funci´on de x
e y en un entorno del punto (0, 0, 0), determina el polinomio de Taylor de grado 2 de dicha funci´on
z(x, y) en el origen y prueba que el origen es un punto cr´ıtico. ¿Qu´e tipo de punto cr´ıtico es?
Ejercicio 4. Considera la superficie S de ecuaci´on x2
+ y2
+ 3xz + 3yz + x + y = 0.
(1) Prueba que dicha ecuaci´on define una funci´on z = f(x, y) cerca de P = (−1, 0, 0).
(2) ¿Es (−1, 0) un punto cr´ıtico de f? Si es as´ı, clasif´ıcalo; si no lo es, di por qu´e.
Ejercicio 5. Sea f(x, y) = (x − cos(y)) ex
− cos(y) un campo escalar de dos variables. Se pide:
(1) Calcular los infinitos puntos cr´ıticos de f y clasificarlos.
(2) Comprobar que f (x, y) = 0 define y como funci´on impl´ıcita y = y(x) cerca de P = (0, π/2).
(3) Hallar la recta tangente a la gr´afica de y = y(x) en el punto P del apartado anterior.
Ejercicio 6. Considera la superficie S de ecuaci´on xez
+ yez
+ z = 1 y el punto P = (0, 0, 1) ∈ S.
(1) Prueba que en un entorno del punto P puede obtenerse la coordenada z de los puntos de
S como una funci´on expl´ıcita z = z(x, y) de las otras dos coordenadas.
(2) Halla la ecuaci´on del plano tangente a S en el punto P.
(3) Halla la recta tangente en P a la curva intersecci´on de S con el cilindro x2
+ (y + 1)2
= 1.
(4) Prueba que (0, 0) es un punto cr´ıtico del campo f(x, y) = z(x, y)+ex+1
+ey+1
y clasif´ıcalo.
Ejercicio 7. Prueba que z3
− 2xy + y = 0 define z como funci´on impl´ıcita de z = z(x, y) en un
entorno de (1, 1, 1) y determina el polinomio de Taylor de segundo orden de z(x, y) en (1, 1).
Halla los valores de los par´ametros α y β para los que el punto (1, 1) es un punto cr´ıtico de la
funci´on g(x, y) = z(x, y) − α(x − 1) + β(y − 1) y clasif´ıcalo.
Ejercicio 8. Considera el punto P = (1, 1, 0) y, para cada valor de un par´ametro α ∈ R, la
ecuaci´on αx2
+ α2
xyz + sen(z) − αxy + x − y = 0.
(1) Comprueba que para cualquier valor de α esta ecuaci´on define impl´ıcitamente z como
funci´on z = zα(x, y) en un entorno del punto P = (1, 1, 0).
(2) Para cada α, calcula el gradiente de zα(A) en el punto A = (1, 1) y escribe la ecuaci´on del
correspondiente plano tangente en el punto P = (1, 1, 0).
(3) Para cada α, determina la direcci´on unitaria ⃗u = (u1, u2) en la que la derivada direccional
D⃗uzα(A) de zα en A = (1, 1) es m´axima e indica su valor.
(4) Halla el valor de α para el cual A = (1, 1) es un punto cr´ıtico del campo zα(x, y) y clasif´ıcalo.
Ejercicio 9. El origen es un punto cr´ıtico del campo escalar definido por f(x, y) = 3x4
−4x2
y+y2
.
Comprueba que a lo largo de cada recta y = mx el origen es un m´ınimo pero que para el campo
dado el origen es un punto de silla (indicaci´on: estudia qu´e ocurre sobre una par´abola y = ax2
).
Ejercicio 10. Del campo escalar f(x, y) = axy2
+ by − 4x3
se sabe que el valor m´aximo de
sus derivadas direccionales en el punto P = (1, 2) es 4 y se alcanza en la direcci´on del vector
⃗u = (0, −1). Halla los valores de las constantes a y b, calcula los puntos cr´ıticos de f y clasif´ıcalos.
Ejercicio 11. Halla y clasifica los puntos cr´ıticos de los siguientes campos escalares.
(1) f(x, y, z) = x4
+ y4
+ z4
− 4xyz (2) f(x, y, z) = x2
+ y2
+ z2
+ xz + 3x − 2y
(3) f(x, y, z) = log(x2
+ y2
+ z2
+ 1) (4) f(x, y, z) = x2
z + xy + 12z − z3

9. 48 Matem´aticas III (GIC y GITI, 2015–2016)
2. EL TEOREMA DE LOS MULTIPLICADORES DE LAGRANGE
Iniciamos en esta secci´on el estudio de los problemas de optimizaci´on con restricciones abordando
el problema de calcular los extremos relativos, m´aximos y m´ınimos, de una funci´on de dos o
tres variables cuando estas variables no son independientes sino que est´an sobre una curva o una
superficie. Este tipo de problemas se conocen gen´ericamente como problemas de optimizaci´on con
restricciones de igualdad.
Problemas de optimizaci´on sobre curvas. Dada la funci´on objetivo f, supongamos que te-
nemos una curva regular a trozos C contenida en el dominio de f y nos planteamos el problema
de hallar los valores m´aximo y m´ınimo que alcanza f sobre los puntos de la curva C.
Este problema puede resolverse por los m´etodos ya conocidos si podemos representar C mediante
una parametrizaci´on ⃗r(t), donde el par´ametro t recorre un cierto intervalo. En ese caso, pasamos a
una funci´on objetivo ϕ(t) = f
(
⃗r(t)
)
de una sola variable y hallamos su m´aximo y su m´ınimo sobre
el intervalo, si existen. A partir de los extremos de ϕ obtenemos los puntos de la curva C en los
que f alcanza sus extremos.
Sin embargo, a veces no se puede hallar una parametrizaci´on de C. En el plano esto ocurre
generalmente cuando C es una curva definida impl´ıcitamente por g(x, y) = 0. En el espacio, ocurre
cuando la curva viene dada como la intersecci´on de dos superficies definidas de forma impl´ıcita.
En esta secci´on abordaremos este tipo de problemas, primero en el caso bidimensional. Despu´es
diremos como se extienden las t´ecnicas al caso tridimensional, tanto para superficies como para
curvas definidas impl´ıcitamente.
Extremos relativos restringidos en el plano. Dada la funci´on objetivo f(x, y), supongamos
que tenemos una curva de ecuaci´on impl´ıcita g(x, y) = 0 contenida en el dominio de f y sea (x0, y0)
un punto de dicha curva.
Optimizaci´on con restricciones de igualdad.
Se dice que f tiene en (x0, y0) un m´aximo relativo sujeto a la restricci´on g(x, y) = 0 si existe un
c´ırculo D centrado en (x0, y0) tal que f(x0, y0) ≥ f(x, y) para todo punto (x, y) ∈ D que cumpla
g(x, y) = 0.
Se dice que f tiene en (x0, y0) un m´aximo relativo sujeto a la restricci´on g(x, y) = 0 si existe un
c´ırculo D centrado en (x0, y0) tal que f(x0, y0) ≤ f(x, y) para todo punto (x, y) ∈ D que cumpla
g(x, y) = 0.
Gen´ericamente, los m´aximos y m´ınimos relativos de la funci´on objetivo f en la curva g(x, y) = 0
se llaman extremos relativos de f sujetos a la restricci´on g(x, y) = 0 o, simplemente, extremos
relativos restringidos y, en algunos textos, extremos relativos condicionados.

10. 3. Optimizaci´on de campos escalares 49
Teorema de los multiplicadores de Lagrange. En las condiciones anteriores, si f y g son
diferenciables en un punto (x0, y0) en el que f tiene un extremo relativo sujeto a la restricci´on
g(x, y) = 0 y Dg(x0, y0) ̸= [0, 0], entonces existe un n´umero λ ∈ R, llamado multiplicador de
Lagrange, tal que
Df(x0, y0) = λDg(x0, y0);
o sea,
∂f
∂x
(x0, y0) = λ
∂g
∂x
(x0, y0) y
∂f
∂y
(x0, y0) = λ
∂g
∂y
(x0, y0).
Geom´etricamente, el teorema de los multiplicadores significa que en un extremo relativo restringido
(x0, y0), son tangentes la curva restricci´on g(x, y) = 0 y la curva de nivel de f que pasa por dicho
punto, f(x, y) = f(x0, y0).
Interpretaci´on geom´etrica del teorema de los multiplicadores de Lagrange.
En la pr´actica, para hallar los extremos relativos de f sujetos a g(x, y) = 0, los puntos candidatos
se obtienen resolviendo un sistema de tres ecuaciones con tres inc´ognitas λ, x e y:
g(x, y) = 0,
∂f
∂x
(x, y) = λ
∂g
∂x
(x, y) y
∂f
∂y
(x, y) = λ
∂g
∂y
(x, y).
Como en el caso de la determinaci´on de los puntos cr´ıticos, la resoluci´on de este sistema de ecua-
ciones puede ser complicada o, en algunos casos, imposible de hacer a mano y, en ese caso, hay
que emplear m´etodos num´ericos para obtener soluciones aproximadas.
Para hallar los valores m´aximo y m´ınimo de f sobre la curva, a los puntos obtenidos resolviendo el
sistema hay que a˜nadir los puntos de la curva g(x, y) = 0 en los que no se puede aplicar el teorema
de los multiplicadores, como los extremos de la curva, los puntos en los que Dg(x, y) no existe o
los puntos en los que se tiene Dg(x, y) = [0, 0].
El m´etodo de los multiplicadores de Lagrange en el caso tridimensional. En el caso
tridimensional, el m´etodo funciona de manera totalmente similar cuando tenemos s´olo una restric-
ci´on g(x, y, z) = 0, lo que corresponder´ıa a trabajar sobre una superficie. Para hallar los extremos
relativos de f(x, y, z) sujetos a g(x, y, z) = 0, los puntos candidatos se obtienen resolviendo un
sistema de cuatro ecuaciones con cuatro inc´ognitas λ, x, y, z:
g = 0,
∂f
∂x
= λ
∂g
∂x
,
∂f
∂y
= λ
∂g
∂y
,
∂f
∂z
= λ
∂g
∂z
.
De nuevo, a los puntos obtenidos resolviendo este sistema hay que a˜nadir los puntos de la superficie
g(x, y, z) = 0 en los que no se puede aplicar el teorema de los multiplicadores, como el borde de la
superficie, los puntos en los que Dg(x, y, z) no existe o los puntos en los que Dg(x, y, z) = [0, 0, 0].

11. 50 Matem´aticas III (GIC y GITI, 2015–2016)
En el caso tridimensional tambi´en puede ocurrir que estemos trabajando en una curva definida
como la intersecci´on de dos superficies de ecuaciones impl´ıcitas g(x, y, z) = 0 y h(x, y, z) = 0.
En ese caso, la condici´on de que el diferencial de la restricci´on no sea cero hay que sustituirla
por una condici´on algo m´as exigente: que los diferenciales de las restricciones sean linealmente
independientes.
Si (x0, y0, z0) es un extremo relativo de la funci´on objetivo f(x, y, z) sujeto a las restricciones
g(x, y, z) = 0 y h(x, y, z) = 0 y los diferenciales Dg(x0, y0, z0) y Dh(x0, y0, z0) son linealmente
independientes, entonces existen sendos multiplicadores λ y µ para cada restricci´on tales que
Df(x0, y0, z0) = λDg(x0, y0, z0) + µDh(x0, y0, z0)
En este caso, los puntos candidatos para ser extremos relativos se obtienen con las soluciones del
correspondiente sistema de cinco ecuaciones con cinco inc´ognitas: x, y, z, λ y µ y, de nuevo, a
estos puntos hay que a˜nadir los extremos de la curva restricci´on y los puntos en los que Dh(x, y, z)
y Dg(x, y, z) no son linealmente independientes o, simplemente, alguno de ellos no existe.
EJERCICIOS DE LA SECCI´ON 2
Ejercicio 1. Determina los posibles extremos relativos de la funci´on f(x, y) = x2
+ y2
sujetos
a la restricci´on 2x + 3y = 6. Dibuja la restricci´on y las curvas de nivel de la funci´on objetivo e
interpreta geom´etricamente el problema.
Ejercicio 2. Determina los posibles extremos relativos de la funci´on f(x, y) = x2
+ y2
siendo
(x, y) puntos de la elipse 5x2
+ 6xy + 5y2
= 8. Dibuja la restricci´on y las curvas de nivel de la
funci´on objetivo e interpreta geom´etricamente el problema.
Ejercicio 3. Determina los posibles extremos relativos de la funci´on f(x, y) = 2(x−3)2
+(y −4)2
siendo (x, y) puntos de la circunferencia unidad. Dibuja la restricci´on y las curvas de nivel de la
funci´on objetivo e interpreta geom´etricamente el problema.
Ejercicio 4. Considera el campo escalar f definido por f(x, y) = y3
+ x2
y + 2x2
+ 2y2
− 4y − 8.
(1) Determina los puntos cr´ıticos de f. ¿Qu´e informaci´on proporciona el criterio de las deriva-
das segundas sobre cada uno de dichos puntos cr´ıticos?
(2) Calcula los candidatos a extremos relativos de f sujetos a la restricci´on x2
+ y2
= 1.
Ejercicio 5. Determina los puntos candidatos a ser extremos relativos de la funci´on f(x, y) = xy
sujetos a la restricci´on x + y = 1
Ejercicio 6. Sea f(x, y, z) = 3x2
+ 4xy + z3
. Determina los puntos candidatos a ser extremos
relativos de f sujetos a x2
+ y2
= 1.
Ejercicio 7. Determina los puntos candidatos a ser extremos relativos de la funci´on f(x, y) = xyz
sujetos a la restricci´on 2x + 4y + z − 6 = 0
Ejercicio 8. Determina los puntos candidatos a ser extremos relativos de la funci´on objetivo
dada por f(x, y) = (x − 1)2
+ y2
+ z2
sujetos a la restricci´on x2
+ (y − 1)2
= z2
e interpreta
geom´etricamente el resultado.
Ejercicio 9. Calcula los puntos candidatos a ser extremos relativos del la funci´on f(x, y, z) = z
sujetos a la curva intersecci´on de la esfera x2
+ y2
+ z2
= 36 con el plano 2x + y − z = 6.

12. 3. Optimizaci´on de campos escalares 51
Ejercicio 10. En los siguientes casos, calcula los puntos candidatos a ser extremos relativos de la
funci´on f(x, y, z) = x2
+ y2
+ z2
sujetos a la restricciones que se dan
(1) x + 3z = 7, x + y + 3z = 9. (2) 2z2
= x2
+ y2
, z = 1 + x + y.
(3) x2
+ 2y2 + 3z2
= 1, 2x2
+ 3y2
+ z2
= 1. (4) x2
+ y2
= 1, 2x + y + z = 4.
3. OPTIMIZACI ´ON CON RESTRICCIONES GENERALES
En las secciones anteriores hemos estudiado c´omo detectar los extremos relativos de un campo
escalar sin restricciones o con restricciones de igualdad; apenas hemos visto nada sobre la existencia
y c´alculo de sus extremos absolutos. Ahora analizaremos la existencia y los procedimientos de
obtenci´on de m´aximos y m´ınimos absolutos de un campo escalar bajo restricciones generales.
Planteamiento general. Sea f la funci´on objetivo, definida en un conjunto abierto U, y supon-
gamos que queremos hallar los valores m´aximo y m´ınimo que puede alcanzar f entre los puntos que
cumplan un conjunto de restricciones que, en general, vendr´an dadas como una o varias igualdades
o desigualdades. Llamaremos D ⊂ U al conjunto de puntos que cumplen las restricciones que se
impongan a las variables (en algunos libros D recibe el nombre de conjunto factible.)
Teorema de Weierstrass. Sea f : U ⊂ R3
→ R un campo escalar continuo y sea D ⊂ U
un conjunto cerrado y acotado contenido en U. Entonces f alcanza en D sus valores m´ınimo y
m´aximo; es decir, existen Pm´ın, Pm´ax ∈ D tales que f(Pm´ın) ≤ f(P) ≤ f(Pm´ax) para todo P ∈ D.
Extremos absolutos. Los valores m´aximo y m´ınimo de f y, por abuso de lenguaje, los puntos
en los que se alcanzan dichos valores, se llaman extremos absolutos, o globales, de f en D.
Procedimiento general para resolver problemas de optimizaci´on. Puede ocurrir que D
no sea cerrado y acotado y, seg´un el comportamiento de f(P) cuando P ∈ U tiende a infinito o a
la frontera de D, que el m´aximo o el m´ınimo absoluto no existan. En otros casos, a pesar de ser
D no acotado, el comportamiento de f permite asegurar que existe el m´aximo o el m´ınimo global
y que ´este se encuentra en un conjunto acotado. Por ejemplo, si queremos hallar el punto de una
curva m´as cercano a un punto dado, entonces aunque la curva no est´e acotada, el m´ınimo siempre
existe y podemos localizarlo en un tramo acotado de la curva fuera del cual podamos asegurar que
la distancia se hace muy grande. Por tanto, el primer paso es, si se puede, reducir el problema al
de encontrar los extremos absolutos de la funci´on objetivo f en un subconjunto cerrado y acotado
D ⊂ U.
En el caso de las funciones de una variable, los puntos candidatos a que en ellos se alcance el m´aximo
o el m´ınimo absoluto de una funci´on en un intervalo cerrado y acotado son los puntos del intervalo
abierto en los que la derivada vale cero y los extremos del intervalo, as´ı que el procedimiento es
calcular estos puntos candidatos y evaluar la funci´on objetivo en ellos para decidir en cu´al(es) se
alcanza el m´aximo absoluto y en cu´al(es) el m´ınimo absoluto.
Para el caso de dos o tres variables, la geometr´ıa del conjunto D puede ser m´as complicada pero en
la pr´actica totalidad de los casos habituales de las aplicaciones, D puede descomponerse f´acilmente
en su frontera, que es donde se cumplen alguna restricci´on de igualdad, y en sus puntos interiores,
que es donde se cumplen las restricciones de desigualdad estricta.
Las dos ideas esenciales ahora son, por un lado, que el conjunto de puntos interiores es abierto,
as´ı que los candidatos a extremos que est´en en el interior de D son los puntos cr´ıticos de f que
est´en en el interior de D — o sea, los que hemos estudiado en la primera secci´on — y, por otro

13. 52 Matem´aticas III (GIC y GITI, 2015–2016)
lado, que la frontera viene dada por los tramos en los que alguna restricci´on es de igualdad, as´ı
que los candidatos a extremos que est´en en la frontera de D son los extremos relativos de f sujetos
a restricciones de igualdad — o sea, los que hemos estudiado en la segunda secci´on —.
Los resultados de las secciones anteriores requieren que la funci´on objetivo sea, al menos, dife-
renciable y, si adem´as queremos usar el test de las derivadas segundas para clasificar los puntos
cr´ıticos, entonces de clase C2
(U), lo que ocurre en la pr´actica totalidad de los casos de inter´es. En
resumen, para determinar los extremos absolutos de una funci´on objetivo de clase C2
(U) sobre un
conjunto cerrado y acotado D se hace, entonces, lo siguiente:
(1) Se descompone D en su frontera y su interior
(2) Se hallan los puntos cr´ıticos de f en el interior de D.
(3) (a) Si son dos variables, entonces la frontera de D es una curva dada por igualdades. Para
hallar los extremos relativos de f en cada tramo de la frontera podemos hacer dos cosas:
– O bien la representamos mediante una parametrizaci´on (x(t), y(t)) y pasamos a una
funci´on objetivo ϕ(t) = f
(
x(t), y(t)
)
de una sola variable, en cuyo caso se hallan los
puntos cr´ıticos de ϕ y con estos valores cr´ıticos del par´ametro se obtienen los puntos
de la frontera en los que f podr´ıa tener un extremo.
– O bien determinamos los candidatos a extremos relativos sujetos a la frontera usando
el teorema de los multiplicadores de Lagrange junto con los puntos en los que el
teorema no sea aplicable.
(b) Si tenemos tres variables, entonces la frontera de D es una superficie o una curva. En
este caso, o bien parametrizamos la frontera, o bien usamos el m´etodo de los multiplicadores
de Lagrange con una o dos restricciones seg´un sea el caso.
(4) Se eval´ua f en todos los puntos obtenidos y se escogen aqu´ellos donde f alcanza el valor
mayor (m´aximo absoluto) y el valor menor (m´ınimo absoluto).
En la siguiente figura vemos un ejemplo de optimizaci´on con restricciones. En rojo se representan
las curvas de nivel de la funci´on objetivo y en azul el conjunto D de las restricciones; azul m´as
claro para el interior y m´as oscuro para la frontera. Los candidatos que est´an en el interior son
los puntos cr´ıticos de la funci´on objetivo: un m´aximo local A, un m´ınimo local B y dos puntos de
silla C. Los candidatos que est´an en la frontera son los seis puntos L dados por el teorema de los
multiplicadores de Lagrange (la frontera y la curva de nivel son tangentes en dichos puntos).
Optimizaci´on con restricciones generales.

14. 3. Optimizaci´on de campos escalares 53
Para descartar errores o ahorrar en los c´alculos, si f es de clase C2
(U), puede ser buena idea
clasificar los puntos cr´ıticos obtenidos en el paso (1) mediante el test de las derivadas segundas; de
esa forma, si en el paso (4) obtenemos un m´aximo global en un punto cr´ıtico que hemos clasificado
como m´ınimo relativo entonces seguramente hay alg´un error en los c´alculos
EJERCICIOS DE LA SECCI´ON 3
Ejercicio 1. Determina los extremos absolutos de la funci´on f(x, y) = 3x2
y2
+ 2x3
+ 2y3
en el
rect´angulo R dado por −2 ≤ x ≤ 1, −5 ≤ y ≤ 1.
Ejercicio 2. Sea f : R2
→ R la funci´on definida por f(x, y) = cos(x) + sen(y). Halla y clasifica
sus puntos cr´ıticos en el interior del cuadrado D dado por 1 ≤ x ≤ 7, 1 ≤ y ≤ 7.
Ejercicio 3. Halla los valores m´aximos y m´ınimos de f(x, y) = y3
+ x2
y + 2x2
+ 2y2
− 4y − 8 en
el cuadrante positivo del c´ırculo unidad.
Ejercicio 4. Determina los extremos absolutos de la funci´on f(x, y) = x2
+y2
+x2
y2
en la regi´on
dada por 4x2
+ y2
≤ 4.
Ejercicio 5. Determina los extremos absolutos de la funci´on f(x, y) = e−(x2
+y2
)
(2x2
+3y2
) sobre
el c´ırculo x2
+ y2
≤ 4.
Ejercicio 6. Determina el rect´angulo de mayor ´area, con lados paralelos a los ejes, que puede
inscribirse en la elipse definida por la ecuaci´on x2
/a2
+ y2
/b2
= 1.
Ejercicio 7. Halla los semiejes de la elipse centrada en el origen 5x2
+ 6xy + 5y2
= 8.
Ejercicio 8. Determina los puntos donde el campo f(x, y) = 4x2
+y2
−4x−3y alcanza sus valores
m´aximo y m´ınimo absolutos en la mitad superior de la elipse 4x2
+ y2
≤ 13.
Ejercicio 9. En los siguientes casos, determina los puntos de la curva m´as pr´oximos al origen de
coordenadas (en los problemas de hallar el m´ınimo o el m´aximo de una distancia es conveniente
tomar como funci´on objetivo el cuadrado de la distancia para evitar la ra´ız cuadrada).
(1) La recta x + y = 4.
(2) La circunferencia de centro (1, 2) y radio r = 8.
(3) El tri´angulo de v´ertices A = (−3, 2), B = (3, 8) y C = (−6, 1).
Ejercicio 10. Calcula las dimensiones de la pir´amide recta de base cuadrada y m´aximo volumen
que puede construirse con un alambre de longitud L.
Ejercicio 11. Calcula los extremos absolutos de la funci´on f(x, y) = xye−xy
en la regi´on D dada
por x2
+ 4y2
≤ 1.
Ejercicio 12. Considera la regi´on D del primer cuadrante limitada por las curvas: y2
− x2
= 1,
x2
− y2
= 1, x + y = 2, x + y = 4. Halla los extremos absolutos de f(x, y) = 2x3
+ y2
en D.
Ejercicio 13. Considera el campo escalar f(x, y) = 3x3
+9xy2
+36x2
+47y+1. Sea S la superficie
de ecuaci´on z = f(x, y) y sea P = (x, y, z) un punto de S. Sabiendo que una de las rectas tangentes
a S en P es paralela a la recta r dada por las ecuaciones x + y = 0 y x − y + z = 0, prueba que las
coordenadas (x, y) de P est´an sobre la par´abola de ecuaci´on x2
+ y2
− 2xy + 8x − 5 = 0 y halla el
punto de esta par´abola m´as cercano al punto (−2, 0).

15. 54 Matem´aticas III (GIC y GITI, 2015–2016)
Ejercicio 14. Considera el campo escalar f(x, y) = y3
+ x2
y + 2x2
+ 2y2
− 4y − 8.
(1) Determina los puntos cr´ıticos de f. ¿Qu´e informaci´on proporciona el criterio de las deri-
vadas segundas sobre cada uno de dichos puntos cr´ıticos?
(2) Calcula los extremos absolutos de f sujetos a la restricci´on x2
+ y2
= 1 usando el Teorema
de los Multiplicadores de Lagrange.
(3) Determina los puntos donde el campo f alcanza sus valores m´aximo y m´ınimo absolutos
en el c´ırculo unidad x2
+ y2
≤ 1.
Ejercicio 15. Sea f(x, y, z) = 3x2
+ 4xy + z3
. Calcula los extremos absolutos de f en el cilindro
S = {(x, y, z) ∈ R3
: x2
+ y2
≤ 1, −2 ≤ z ≤ 2}.
Ejercicio 16. Calcula el m´aximo y el m´ınimo absolutos de f(x, y, z) = x2
+ y2
+ z2
+ x + y + z
sobre el conjunto D = {(x, y, z) : x2
+ y2
+ z2
≤ 1, y + z = 1}.
Ejercicio 17. Prueba que los ´angulos de un tri´angulo cumplen sen(x) + sen(y)+ sen(z) ≤ 3
√
3/2.
Ejercicio 18. Calcula los extremos absolutos de f(x, y, z) = x + 3xy − z2
en la esfera unidad.
Ejercicio 19. Determina los extremos absolutos de la funci´on f(x, y, z) = x2
+ yz en la regi´on
definida por x2
+ y2
≤ z ≤ 1.
Ejercicio 20. Una sonda espacial con forma esf´erica de radio 6 unidades entra en la atm´osfera y
su superficie empieza a calentarse. Pasada una hora, la temperatura en un punto (x, y, x) de su
superficie es de T(x, y, z) = 6x − y2
+ xz + 60. Determina los puntos de la superficie de la sonda
m´as fr´ıos y m´as calientes. Razona en ambos casos por qu´e podemos garantizar su existencia.
Ejercicio 21. Encuentra el punto m´as alto de la circunferencia definida por la intersecci´on de la
esfera x2
+ y2
+ z2
= 36 con el plano 2x + y − z = 6.
Ejercicio 22. En los siguientes casos, determina los puntos de la curva m´as pr´oximos al origen
de coordenadas
(1) La intersecci´on del cono 2z2
= x2
+ y2
con el plano z = 1 + x + y.
(2) La curva dada por la intersecci´on de los elpsoides x2
+ 2y2 + 3z2
= 1 y 2x2
+ 3y2
+ z2
= 1.
(3) El tri´angulo de v´ertices A = (−3, 2, 2), B = (3, 8, −4) y C = (−6, 1, 0).
Ejercicio 23. Encuentra el punto del cono z2
= x2
+ (y − 1)2
m´as cercano al punto P = (1, 0, 0).
Ejercicio 24. Encuentra las dimensiones ´optimas de un recipiente con forma de caja sin tapa de
superficie dada a.
Ejercicio 25. Encuentra las dimensiones ´optimas de un recipiente con forma de caja sin tapa de
volumen dado v.
Ejercicio 26. Halla las distancias m´axima y m´ınima desde el origen hasta la curva dada por la
intersecci´on de los elipsoides x2
+ 2y2
+ 3z2
= 1 y 2x2
+ 3y2
+ z2
= 1.
Ejercicio 27. Calcula el punto m´as cercano al eje OY de la elipse dada por la intersecci´on del
cilindro x2
+ 2y2
= 1 con el plano 3x = 4z.
Ejercicio 28. Calcula los extremos absolutos del campo escalar f(x, y, z) = x − y − z sobre la
elipse dada por la intersecci´on del cilindro 2x2
+ y2
= 4 con el plano x + y + z = 1.

16. 3. Optimizaci´on de campos escalares 55
Ejercicio 29. Cortando el paraboloide z = 4−x2
−y2
con el plano z = y +2 se obtiene una curva
C. Adem´as, sea V el s´olido formado por el trozo acotado de los dos en que dicho corte divide al
paraboloide.
Los elementos geom´etricos descritos.
(1) Calcula la recta tangente a C en el punto P = (0, 1, 3).
(2) Calcula el plano tangente al paraboloide en dicho punto P.
(3) Calcula la recta tangente al paraboloide en el punto P que tiene pendiente m´axima.
(4) Utilizando el teorema de los multiplicadores de Lagrange, prueba que P = (0, 1, 3) es el
punto m´as alto de la curva C.
Ejercicio 30. De los puntos que est´an a la vez en el cilindro x2
+ y2
= 1 y en la superficie
z2
− xy = 0, calcula, en el caso de que existan, el que est´a m´as cerca y el que est´a m´as lejos del
origen de coordenadas.
Ejercicio 31. La ecuaci´on x2
+ 3y2
− 2xy = 1 representa una elipse centrada en el origen de
coordenadas. Aplica el teorema de los multiplicadores de Lagrange para hallar sus semiejes.
Ejercicio 32. Sea S la superficie dada en R3
por z3
+ zx3
+ zy4
+ y2
+ 2xy − 2x − 4y + 3 = 0.
(1) Prueba que en un entorno del punto P = (1, 1, 0) puede obtenerse la coordenada z de los
puntos de S como una funci´on expl´ıcita z = f(x, y) de las otras dos coordenadas.
(2) Calcula el polinomio de Taylor de grado 2 de f en el punto (1, 1).
(3) Prueba que (1, 1) es un punto cr´ıtico de f y clasif´ıcalo.
(4) Sea C la intersecci´on de S con el plano XY . Para hallar los extremos relativos del campo
g(x, y) = x(y − 1) sujetos a la restricci´on C, ¿cu´ales son los puntos candidatos a extremos
relativos que proporciona el teorema de los multiplicadores de Lagrange para este caso?
(5) Halla los extremos absolutos de g sujetos a la restricci´on C.
Algunas notas hist´oricas. Los problemas de optimizaci´on — el c´alculo de m´aximos y m´ınimos — forman parte de
las matem´aticas, y de sus aplicaciones a la mec´anica y la ingenier´ıa, desde sus or´ıgenes. Por ejemplo, los astr´onomos
de Babilonia ya se dieron cuenta que los planetas parec´ıan detenerse cuando aparentaban estar lo m´as lejos o cerca
posible. La leyenda de la reina Dido, fundadora de Cartago, cuenta c´omo resolvi´o, mediante una circunferencia,
el problema de rodear una cantidad lo m´as grande posible de terreno cuando el per´ımetro est´a dado. Este y otros
problemas de optimizaci´on fueron resueltos por los ge´ometras griegos. Por ejemplo, Her´on descubri´o, en torno al
siglo i ac, que la luz se refleja siguiendo el camino m´as corto.
Con la invenci´on del c´alculo infinitesimal se desarrollaron los primeros m´etodos sistem´aticos para resolver problemas
de optimizaci´on. As´ı, Pierre de Fermat fue el primero, en 1636, en postular que la derivada vale cero en los extremos
locales de una funci´on de una variable. Tambi´en mostr´o en 1657 que la ley de Snell es una consecuencia de que la
luz viaja siguiendo el camino m´as corto tambi´en cuando se refracta al pasar de un medio a otro, aire y agua, por
ejemplo, en el que viaja a diferente velocidad. En 1696 Johann y Jacob Bernoulli y Newton plantean y resuelven al
problema de la braquistocrona: la propiedad que tiene la cicloide de ser la curva por la que un m´ovil sujeto a la acci´on
de la gravedad pasa en el menor tiempo posible de un punto a otro, ambos situados en un mismo plano vertical.

17. 56 Matem´aticas III (GIC y GITI, 2015–2016)
Este resultado y otros en problemas similares permiten a Leonhard Euler formular en 1740 los primeros criterios de
optimalidad de curvas y superficies, lo que se conoce como el c´alculo de variaciones. Joseph Louis Lagrange resolvi´o
en 1755 algunas cuestiones planteadas por Euler, y su colaboraci´on culmin´o con la formulaci´on de las ecuaciones
de Euler-Lagrange que son el punto central de la teor´ıa del c´alculo de variaciones. En paralelo, Lagrange formul´o
en 1759 el test de las derivadas segundas para funciones de dos variables y tambi´en fue de los primeros en estudiar
problemas de optimizaci´on con restricciones, formulando en 1788 su teorema de los multiplicadores.
A lo largo del siglo xix y primera mitad del xx se establecen los fundamentos te´oricos de la disciplina y se formulan
m´etodos num´ericos para resolver problemas de optimizaci´on. En 1806 Adrien M. Legendre y Carl F. Gauss inventan
el m´etodo de los m´ınimos cuadrados. Bernard Bolzano (1830, para funciones de una variable) y Karl Weierstrass
(1860, para varias variables) formulan la condici´on suficiente para la existencia de extremos; Carl Gustav Jacobi,
en 1850, y James Joseph Sylvester, en 1852, dan la clasificaci´on de las cu´adricas seg´un los signos de los autovalores,
extendiendo el resultado de Lagrange a campos de varias variables. Augustin Cauchy formula en 1857 el m´etodo
del descenso m´as r´apido.
La aparici´on de los computadores a mediados del siglo xx dieron un enorme impulso a los m´etodos num´ericos
para resolver problemas de optimizaci´on que son esenciales en la ingenier´ıa. Se˜nalemos, sobre todo, el m´etodo del
s´ımplex que permite resolver problemas de optimizaci´on lineales de muchas variables sujetas a restricciones lineales,
inventado de forma independiente por Leonid V. Kantorovich en 1939 y George Dantzig en 1947. Este y otros
m´etodos ser´an estudiados en las asignaturas “M´etodos Matem´aticos”, “Estad´ıstica e Investigaci´on Operativa” y, en
GITI, “M´etodos Cuantitativos de Organizaci´on Industrial”.
BIBLIOGRAF´IA
G.L. Bradley y K.J. Smith, C´alculo, vol. 2, Cap´ıtulo 12.
R.E. Larson, R.P. Hostetler y B.H. Edwards, C´alculo, vol. 2, Cap´ıtulo 12.
G.B. Thomas, Jr., C´alculo, varias variables, Cap´ıtulo 14.
P´aginas web de inter´es:
http://www.wolframalpha.com
http://web.monroecc.edu/manila/webfiles/calcNSF/JavaCode/CalcPlot3D.htm
http://www.desmos.com/