invariancia.pptx
•Descargar como PPTX, PDF•
0 recomendaciones•12 vistas
algebra lineal
Denunciar
Compartir
Denunciar
Compartir
Recomendados
Más contenido relacionado
Similar a invariancia.pptx
Similar a invariancia.pptx (20)
Transormaciones Lineales - Gabriela bello - Algebra lineal

Transormaciones Lineales - Gabriela bello - Algebra lineal
Algebra lineal ESPOL-folleto 2do parcial-ramiro-saltos

Algebra lineal ESPOL-folleto 2do parcial-ramiro-saltos
Daymarian Tauil - Transformaciones lineales - Algebra lineal - Saia

Daymarian Tauil - Transformaciones lineales - Algebra lineal - Saia
Aplicar derivadas en el cálculo de velocidad y aceleración de un objeto que s...

Aplicar derivadas en el cálculo de velocidad y aceleración de un objeto que s...
Último
Último (20)
herrramientas de resistividad para registro de pozos.pptx

herrramientas de resistividad para registro de pozos.pptx
Sesión de Clase A dde sistemas de riego y otras obras

Sesión de Clase A dde sistemas de riego y otras obras
707555966-El-Libro-de-La-Inteligencia-Artificial-Version-11-Alfredovela.pdf

707555966-El-Libro-de-La-Inteligencia-Artificial-Version-11-Alfredovela.pdf
subestaciones electricas , elementos y caracteristicas

subestaciones electricas , elementos y caracteristicas
Diseno de Estructuras de Acero - 5ta Ed - McCormac.pdf

Diseno de Estructuras de Acero - 5ta Ed - McCormac.pdf
Circuitos_basicos_de_neumatica miquel carulla .pdf

Circuitos_basicos_de_neumatica miquel carulla .pdf
invariancia.pptx
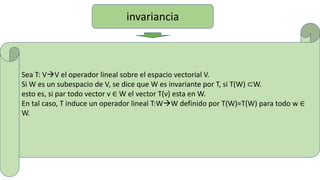
- 1. invariancia Sea T: VV el operador lineal sobre el espacio vectorial V. Si W es un subespacio de V, se dice que W es invariante por T, si T(W) ⊂W. esto es, si par todo vector v ∈ W el vector T(v) esta en W. En tal caso, T induce un operador lineal T:WW definido por T(W)=T(W) para todo w ∈ W.
- 2. Por ejemplo: Tenemos que 𝑇 𝑤1 ⊂ 𝑤1,entonces 𝑤1es invariante por T. pero también se cumple: 𝑇 𝑤2 ⊂ 𝑤2 , entonces 𝑤2 es invariante por T. Cuando V es de dimensión finita , la invariancia de W por T tiene una interpretación matricial simple, muy interesante que la mencionamos en el siguiente teorema : Supongamos que W es un subespacio invariante de T:VV. entonces T tiene una representación matricial por bloques 𝑏 𝑐 0 𝑑 , donde B es una representación matricial de restricción T de T en W. TEOREMA
- 3. EJEMPLO: Sea la matriz donde la traz(A)=4 y det(A)=-5 a) El polinomio característico de A es: p(x) = 𝑥2 − (𝑡𝑟𝑎𝑧 𝐴)𝑥 + 𝑑𝑒𝑡 𝐴 p(x) = 𝑥2 − 4𝑥 − 5 p(x) = (x-5)(x+1) b) Los valores propios de la matriz a 𝑥1 = 5 𝑦 𝑥2 = −1 se obtienen resolviendo las ecuaciones homogéneas. • Vector propio asociado a 𝑥1 = 5 RESOLVER: ( A – 5I ) U = 0 el subespacio propio asociado al valor propio 𝑥1 = 5 es: es una recta en que pasa por el origen (1,1) y es el vector d 𝐴 = 1 4 2 3
- 4. • Vector propio asociado a 𝑥2 = −1 El subespacio propio asociado al valor propio 𝑥2 = −1 es: RESOLVER: ( A + I ) V = 0 esta es una recta en que pasa por el origen y (2,-1) es el vector director
- 5. i) eligiendo el polinomio lineal g(x) = x - 5 se obtiene: El operador g(T) = T - 5I La matriz g(A) = A - 5I = −4 4 2 −2 Eligiendo cualquier vector 𝛼 ∈ ℝ2 se cumple la siguiente propiedad: g(T)𝛼 esta en 𝑤2 = 𝑠 2 −1 , 𝑠 ∈ ℝ esta propiedad nos indicara que: “el T-conductor de 𝛼 en 𝑤2 es el polinomio Mónico g(x) = x – 5” ii) eligiendo el polinomio lineal g(x) = x + 1 se obtiene: El operador h(T) = T + I La matriz h(A) = A + I = 2 4 2 4 Eligiendo cualquier vector 𝛼 ∈ ℝ2 se cumple la siguiente propiedad: h(T)𝛼 está en 𝑤2 = 𝑡 1 −1 , 𝑡 ∈ ℝ esta propiedad nos indicara que: “el T-conductor de 𝛼 en 𝑤1 es el polinomio Mónico h(x) = x + 1”