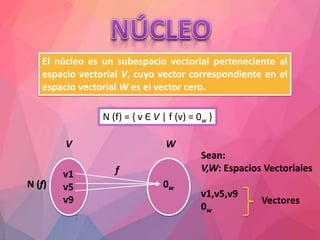
1) Las transformaciones lineales son funciones entre espacios vectoriales que preservan las operaciones vectoriales. 2) Se pueden representar mediante matrices y describen cambios de base en los espacios vectoriales. 3) Juegan un papel fundamental en álgebra lineal y sus aplicaciones en diversas áreas como matemáticas, física e ingeniería.

1. Elba Alcalá
C.I. 26.436.611

2. Las transformaciones lineales son las funciones y tratan sobre K-
espacios vectoriales que son compatibles con la estructura (es
decir, con la operación y la acción) de estos espacios.
Sean V y W dos espacios vectoriales posiblemente iguales.
Una transformación lineal o mapeo lineal de V a W es una
función
T : V → W tal que para todos los vectores u y v de V y
cualquier escalar c:
a) T (u + v) = T (u) + T (v)
b) T (c u) = c T (u)
Una transformación lineal es una función entre espacios vectoriales, es
decir, el objetivo es transformar un espacio vectorial en otro.

3. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores
y realizar un diagrama.
f : P(2) R2
(a+bx+cx2 ) f (a+bx+cx2 ) = (a-b, 2c+a )
P(2)
(a+bx+cx2 )
R2
f (a+bx+cx2 ) = (y, z)
f
f (1-x) = (2,1)
f (3+x-2x2) = (2,-1)
f (0+0x+0x2) = (0,0)
(1-x)
(3+x-2x2)
(0+0x+0x2)
V1
V2
V3
Solución:
1

4. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores y
realizar un diagrama.
f : R3 R2
(x, y, z ) f (x, y, z) = (2x+y+3z, -x+2y+4z)
R3 R2
f(x, y, z ) f (x, y, z ) = (a, b)
(1,3,2)
(3,5,1)
(0,0,0)
f (1,3,2) = (11, 13)
f (3,5,1) = (14, 11)
f (0,0,0) = (0,0)
V1
V2
V3
Solución:
2

5. Dada la siguiente aplicación lineal, obtener la imagen de tres vectores y
realizar un diagrama.
f : R3 M2
(x, y, z ) f (x, y, z) =
x+y-z x+3y+2z
2x+y-3z -3x+2y+3z
(1,0,1)
(-2,3,1)
(0,0,0)
f (1,3,2) =
f (3,5,1) =
f (0,0,0) =
V1
V2
V3
0 3
-1 0
0 9
-4 15
0 0
0 0
R3
(x, y, z )
M2
f (x, y, z ) =
f a b
c d
Solución:
3

6. Es un algoritmo del álgebra lineal para
determinar las soluciones de un sistema de
ecuaciones lineales, encontrar matrices e
inversas. Un sistema de ecuaciones se
resuelve por el método de Gauss cuando se
obtienen sus soluciones mediante la
reducción del sistema dado a otro
equivalente en el que cada ecuación tiene
una incógnita menos que la anterior.
Transforma la matriz de coeficientes en una
matriz triangular superior y el método de
Gauss-Jordan continúa el proceso de
transformación hasta obtener una matriz
diagonal

7. 1
2

8. 3

9. El núcleo es un subespacio vectorial perteneciente al
espacio vectorial V, cuyo vector correspondiente en el
espacio vectorial W es el vector cero.
.
.
.
.
.
.
f
V W
v1
v5
v9
0wN (f)
Sean:
V,W: Espacios Vectoriales
v1,v5,v9
0w
Vectores
N (f) = { v Є V | f (v) = 0w }

10. Dada la siguiente aplicación lineal, realice un diagrama, y escriba la
definición de núcleo.
f : R2 R3
(x, y) f (x, y) = (x-y,2x, y+x)
R2
(x, y)
R3
f (x, y) = (a, b, c)
f
N f : {x, y / f (x, y) = (x-y,2x, y+x) = (0,0,0)}
1 -1 0
2 0 0
1 1 0
x-y = 0
2x = 0
y+x = 0
y = 0
x = 0
N f : {(x, y)/ x = 0 y = 0}
<N f : {(0, 0)}
En este caso, el núcleo de la función es el cero
vector.
Solución:
1

11. Sean V, W espacios vectoriales sobre un campo F y sea T ∈ L(V, W). La imagen de
T se define como el conjunto de todos los valores de la aplicación T:
im(T) := {ɯ ∈ W : ∃v ∈ V tal que ɯ = T(v)}.
f: R3 → R 3 definida como f(x1, x2, x3) = (x1 − x2, −x1 + x2, 2x1 − 2x2 +
x3).
Im(f) = {y ∈ R 3 / ∃ x ∈ R 3 , f(x) = y}
= {y ∈ R 3 / ∃ (x1, x2, x3) ∈ R3 , (x1 − x2, x1 − x2, 2x1 − 2x2 + x3) = y}.
y = (x1 − x2, −x1 + x2, 2x1 − 2x2 + x3)
= (x1, −x1, 2x1) + (−x2, x2, −2x2) + (0, 0, x3)
= x1.(1, −1, 2) + x2.(−1, 1, −2) + x3.(0, 0, 1).
Im(f) = < (1, −1, 2),(−1, 1, −2),(0, 0, 1) > = < (1, −1, 2),(0, 0, 1) >
1 Hallar la imagen de la transformación lineal

12. Sean V, W espacios vectoriales sobre un campo F y sea
T ∈ L(V, W). El rango de T se define como la dimensión
de la imagen de T:
r(T) = dim(im(T)).
Determine el rango y el espacio de los renglones de A.
1

13. Sean V, W espacios vectoriales sobre un campo F y sea T ∈
L(V, W). La nulidad de T se define como la dimensión del
núcleo de T:
nul(T) = dim(ker(T)).
Determine le rango y nulidad para las siguientes matrices
1

14.  TEOREMA 1
Sea A una matriz de m x n . Entonces la transformación
matricial TA: Rn Rm definida por.
TA(x) = A x (para x en Rn)
es una transformación lineal.
 TEOREMA 2
Sea T: Rn Rm una transformación lineal. Entonces T
es una transformación matricial. Mas específicamente, T = TA,
donde A es la matriz de m x n
 A =
Esta matriz se la conoce como matriz estándar de la
transformación lineal T
T(e1); T(e2); ... ; T(en)

15. TEOREMA 3
Sean T: Rm Rn y S: Rn Rp transformaciones lineales. Entonces
S T: Rm Rp es una transformación lineal. Además, sus matrices estándar se
encuentran relacionadas mediante
S T = S T
• TEOREMA 4
Sea T: Rn Rn una matriz invertible. Entonces su matriz
estándar (T) es una matriz invertible, y (T-1)= (T -1).

16. Se puede determinar el núcleo, la imagen, la
nulidad y el rango de una transformación lineal
de Rn-Rm determinando el espacio nulo y la
imagen de la matriz correspondiente.
Adicionalmente, una vez que se sabe que
Tx = Ax. Se puede evaluar Tx para cualquier x
en Rn mediante una simple multiplicación de
matrices.
Pero esto no es todo, cualquier transformación
lineal entre espacios vectoriales de dimensión
finita se puede representar mediante una
matriz.

17. Las transformaciones lineales son
mapeos de importancia fundamental en
el álgebra lineal y en sus
aplicaciones. Desempeñan un papel
muy importante en muchos ámbitos
como lo son las matemáticas, física,
ingeniería, procesamiento de imágenes,
graficas en computadora y muchas otras
áreas de la ciencia y la vida diaria.
Después de realizar este trabajo se
puede concluir que los temas vistos
anteriormente durante el semestre son
importantes dentro de las
transformaciones lineales.

18. http://ima.ucv.cl/
http://ima.ucv.cl/
http://ima.ucv.cl/
http://www.virtual.unal.edu.co/
http://www.matem.unam.mx/
http://www.ciencia.net/
http://html.rincondelvago.com/