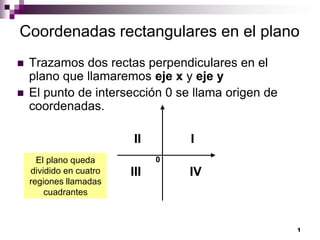
1. 1
Coordenadas rectangulares en el plano
 Trazamos dos rectas perpendiculares en el
plano que llamaremos eje x y eje y
 El punto de intersección 0 se llama origen de
coordenadas.
II I
III IV
0El plano queda
dividido en cuatro
regiones llamadas
cuadrantes

2. 2
Representación de los números
sobre cada eje

3. 3
Coordenadas de un punto
 A un punto P del plano le asociamos dos números de la
siguiente manera
 Decimos que P tiene coordenadas (Q,R)
 La primera se llama abscisa y la segunda ordenada de P.
 Recíprocamente, dado un par de números (Q,R) hay un
número P del plano del cual son las coordenadas.

4. 4
Ejemplo
 Representación de los puntos P=(1/2,1) y
P´=(-3,2)

5. 5
Ejemplo 2
 Conjunto de puntos P=(x,y) cuyas coordenadas
verifican x>2 e y ≤ -1
A={(x,y) : x>2 ; y ≤ -1}
 Representación

6. 6
Ejercicio 1
 Representar en el plano los siguientes
pares ordenados y decir a qué cuadrante
pertenecen
(2, -1) ; (-1/2 ,3) ; (5/3, -2) ; (-1, -2)

7. 7
Ejercicio 2
A. ¿Qué signo tienen las coordenadas de un
punto del segundo (respectivamente cuarto)
cuadrante?
B. Sombrear la parte del plano que corresponde
a los puntos de abscisa negativa.
C. Sombrear la parte del plano cuya abscisa es
positiva y cuya ordenada es negativa.

8. 8
Ejercicio 3
A. Representar el triángulo de vértices
A=(0,0), B=(3,0) y C=(2,3) y evaluar su
área.
B. Hacer lo mismo para A=(1,0), B=1,3) y
C=(0,1)

9. 9
Ejercicio 4: Representar gráficamente
A = { (x,y) : x > 1 }
B = { (x,y) : y ≤ 0 }
C = { (x,y) : x . y = 0 }
D = { (x,y) : 1 ≤ x ≤ 2 , y > 0 }
E = { (x,y) : x = y }
F = { (x,y) : x . y < 0 }

10. 10
Ejercicio 5
 Definir mediante condiciones los siguientes
subconjuntos del plano

11. 11
Ejercicio 5 (cont)
 Definir mediante condiciones los siguientes
subconjuntos del plano

12. 12
Rectas en el plano
 Ejemplo : El conjunto de ptos.de plano de
abscisa 3.
L = { (x,y) : x = 3 }

13. 13
Rectas en el plano
 Ejemplo : El conjunto de puntos cuya
abscisa coincide con la ordenada.
L = { (x,y) : x = y }

14. 14
Rectas en el plano
 Ejemplo : La recta horizontal (paralela al
eje x) que pasa por P0=(1,2)
L = { (x,y) : y = 2 }

15. 15
Rectas en el plano
 Sea L la recta que pasa por P1=(1,2) y P2=(3,5)
13
1
25
2 xy
Operando
2y – 3x = 1

16. 16
Ecuación de la recta
 Si L es vertical, tiene ecuación x=c
L = { (x,y) : x = c }
 Si L es horizontal, tiene ecuación y=c
L = { (x,y) : y = c }

17. 17
Ecuación de la recta
 Si L no es ni horizontal ni vertical y pasa por los
puntos P1=(a1,b1), P2=(a2,b2) tiene ecuación
que operando se escribe de la forma
Ax + By = C
12
1
12
1
bb
by
aa
ax

18. 18
Ejercicio 7
 Hallar la ecuación de la recta que pasa
por los puntos dados:
A. (2,3) ; (4,5)
B. (5,-1) ; (-5,-1)
C.(½, ½) ; (0,0)
D.(1,-1) ; (-1,1)

19. 19
Ejercicio 8
 Sea L la recta que pasa por P1=(-1, 0), P2=(5, 1)
a) Hallar la ecuación de L y comprobarla.
b) Mostrar otros dos puntos de L.
c) ¿Cuáles de los siguientes puntos
pertenecen a L?
Q1 = (3, ½) ; Q2 = (10,2) ; Q3 = (-7, -1)

20. 20
Ejercicio 9
 Hallar el valor de k para el cual los puntos
(-1,2) ; (3,1) ; (2, -k+1)
están alineados

21. 21
Ecuación de la recta
 Dada una ecuación de la forma
Ax + By = C {A 0 o B 0}
veremos que los puntos P=(x,y) que la
verifican forman una recta.

22. 22
Ecuación de la recta
 Dada una ecuación de la forma
Ax + By = C
CASO 1 : A = 0, la ecuación se escribe
es una recta horizontal
B
C
y

23. 23
Ecuación de la recta
 Dada una ecuación de la forma
Ax + By = C
CASO 2 : B = 0, la ecuación se escribe
es una recta vertical
A
C
x

24. 24
Ecuación de la recta
 CASO 3 : A 0 y B 0
 La ecuación de la recta que pasa por los puntos
P1 = (0, a) y P2 = ( 1, a+b) es
B
C
b
B
A
adondebxay ;
baxy
a
by
x
bba
byx
01
0
Los puntos que verifican esta ecuación forman la
recta que pasa por P1 y P2.

25. 25
Ejemplo
 Si queremos representar en el plano el
conjunto de puntos
{(x,y) : 2x – y = -1}
 Sabemos que se trata de una
recta determinada por dos puntos.
Ej : P1 = (0,1) ; P2 = (1,3)

26. 26
Ejercicio 10
 Representar gráficamente
A) 5x + y = 3
B) x – 2 = 0
C) 4x – 3y = 6
D) y = 0

27. 27
Posición Relativa de dos rectas
Transversales Paralelas Coincidentes

28. 28
Sistema de Ecuaciones
 Dadas dos rectas, cada una de ellas está
representada por una ecuación lineal.
 Los puntos de intersección deben verificar
ambas ecuaciones
A1x + B1y = C1
A2x + B2y = C2

29. 29
Sistema de Ecuaciones
 Decir que las rectas son transversales es lo
mismo que decir que el sistema de ecuaciones
tiene una única solución.
 Decir que son paralelas equivale a decir que el
sistema no tiene solución.
 Decir que son coincidentes es lo mismo que
decir que las dos ecuaciones son
equivalentes.

30. 30
Ejemplo 1
 Sean las rectas de ecuaciones
L1 : 2x – y = -1
L2 : x – y = 2
El sistema admite una única solución
Por lo tanto, las rectas son transversales y se cortan en
3
5
;
3
1
yx
3
5
,
3
1
P

31. 31
Ejemplo 1

32. 32
Ejemplo 2
 Sean las rectas de ecuaciones
L1 : 2x – y = – 3
L2 : – 6x + 3y = – 6
 Multiplicando la primer ecuación por -3 obtenemos
un sistema equivalente
6x – 3y = – 9
6x – 3y = – 6
 Restando ambas ecuaciones obtenemos 0= – 15 lo
cual no puede ser. El sistema NO tiene solución.

33. 33
Ejemplo 2

34. 34
Ejemplo 3
 Sean las rectas de ecuaciones
L1 : 4x – 8y = -12
L2 : – x + 2y = 3
 Multiplicando la segunda ecuación por -4 obtenemos
la primera. Es decir, ambas ecuaciones en realidad
son la misma ecuación. Las rectas coinciden.

35. 35
Distancia entre dos puntos del plano
 Dados dos puntos del plano
P1 y P2
 Podemos calcular la distancia entre ellos por el teorema
de Pitágoras
2
12
2
12
)()( yyxxd

36. 36
Ejemplo
 Calcular la distancia entre
P1=(3,2) y P2=(1,-4)
40364
)24()31(
22
d
d