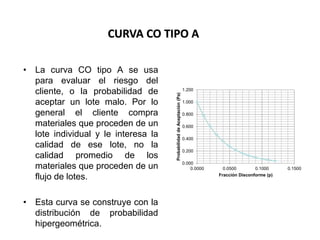
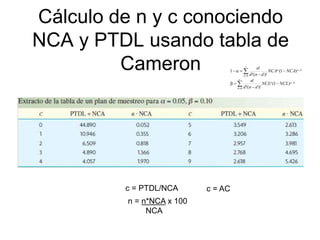
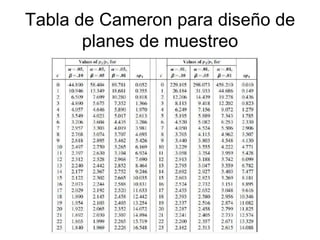
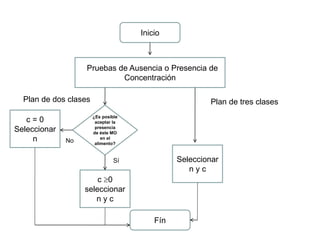
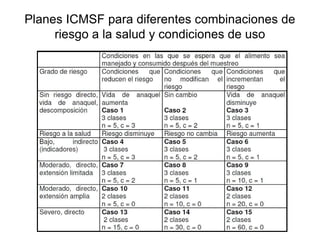
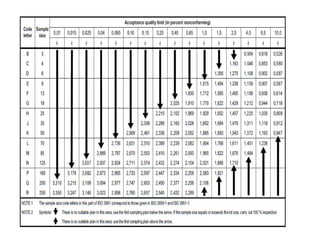
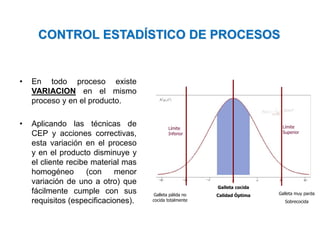
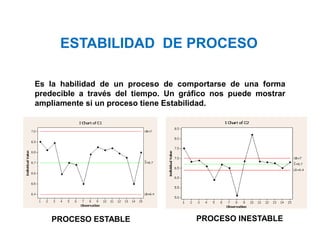
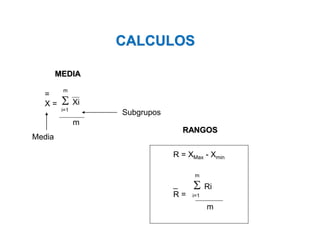
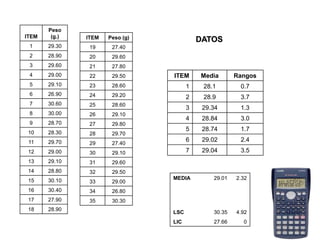
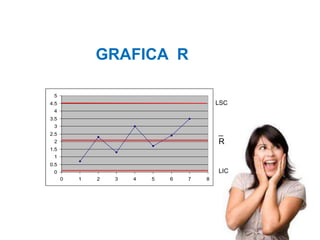
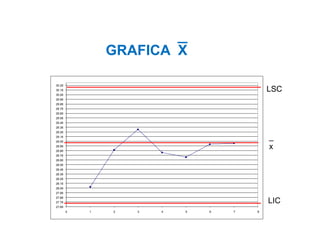
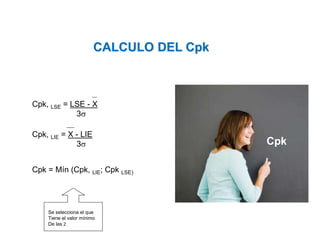
El documento trata sobre el muestreo de aceptación. Explica que este tipo de muestreo se realiza sobre lotes de productos terminados para decidir su aceptación o rechazo basándose en una muestra. También define la curva operativa y explica que muestra la probabilidad de aceptar un lote para diferentes valores de fracción defectuosa. Finalmente, incluye un ejemplo de cálculo de probabilidad de aceptación usando la distribución hipergeométrica.