02__Repaso_de_Tratamiento_de_Errores_y_Ajuste_de_Datos.pdf

Universidad Nacional Autónoma de Honduras
Departamento de Física UNAH-VS
Práctica 2
FS415
REPASO DE TRATAMIENTO DE
ERRORES Y AJUSTE DE DATOS
I Periodo Académico 2024
Objetivos
1. Emplear correctamente las cifras significativas.
2. Calcular la incertidumbre absoluta mediante el método diferencial de mediciones indirectas.
3. Desarrollar el proceso completo de regresión lineal de forma manual y de forma semi-
automática con el uso del software Mathematica.
4. Interpretar el significado de la pendiente e intercepto según las ecuaciones empíricas.
Mediciones
La medición es el proceso por el cual cuantificamos nuestra experiencia con el mundo exterior.
Existen dos tipos de mediciones:
1. Mediciones directas: aquellas que se han realizado con instrumentos que han sido calibrados
para tomar la medición de interés. Como usar una regla, un pie de rey, o una balanza.
2. Mediciones indirectas: aquellas que se obtienen mediante el uso de alguna formula matemática
haciendo uso de las mediciones directas. Como el volumen de un cubo calculado a partir de
sus dimensiones.
Aunque es imposible conocer todas las causas del error es conveniente conocer todas las causas
importantes y tener una idea que permita evaluar los errores más frecuentes. Las principales causas
que producen errores se pueden clasificar en:
Error debido al instrumento de medida: Son aquellos debido al diseño y fabricación de los
instrumentos. Con el paso del tiempo a estas se les añade las imperfecciones por desgaste.
Error debido al operador: Es aquel debido a la imperfección de los sentidos de un operador
o la habilidad que posee este para efectuar las mediciones.
Error debido a los factores ambientales: Estos son debidos a factores externos. Algunos de
ejemplos de estos son la dilatación lineal debido a la temperatura, la humedad, el polvo, la
suciedad, etc.
1

Práctica 2
FS415
Cifras Significativas
En cualquier medición, las cifras significativas son los dígitos que se conocen con certeza, más
un dígito que es incierto. Existen varias reglas para determinar que dígitos de un numero son
significativas y cuales no. Los dígitos en negrita son significativos.
1. En números que no contienen ceros, todos los dígitos son significativos. Ejemplos:
3.142 cuatro cifras significativas
467 tres cifras significativas
2. Todos los ceros entre dígitos significativos son significativos. Ejemplos:
3. Los ceros a la izquierda del primer dígito que no es cero sirven solamente para fijar la posición
del punto decimal y no son significativos. Ejemplos:
0.56 dos cifras significativas
0.0789 tres cifras significativas
4. En un número con dígitos a la derecha del punto decimal, los ceros a la derecha del último
número diferente de cero son significativos. Ejemplos:
0.00200 tres cifras significativas
5. En un número que no tiene punto decimal y que termina con uno o más ceros (como 3600),
los ceros con los cuales termina el número pueden ser o no significativos. El número es
ambiguo en términos de cifras significativas. Antes de poder especificar el número de cifras
significativas, se requiere información adicional acerca de cómo se obtuvo el número. Si el
número es resultado de una medición, los ceros probablemente no son significativos. Si el
número ha sido contado o definido, todos los dígitos son significativos. Para esta práctica
estos ceros no serán significativos. Ejemplos:
3600 dos cifras significativas
6. Cuando un numero este expresado en notación científica todos los dígitos son significativos.
Ejemplos:
5.60×103
3 cifras significativas
1×105
1 cifra significativa
6.000×102
4 cifras significativas
2

Práctica 2
FS415
Redondear en Mathematica
Para redondear un número en Mathematica se utiliza el comando Round[x,a], donde x es
el numero que se desea redondear y a es el múltiplo mas cercano donde se quiere redondear.
Otro código que utiliza comúnmente para establecer precisión en números es SetPrecision.
Cifras Significativas en Operaciones Matemáticas
Adición y sustracción
Cuando los números se sumen o resten, el número de lugares decimales en el resultado debe ser
igual al número más pequeño de lugares decimales de cualquier término en la suma. Ejemplos:
5.32 + 6.1 = 11.42 ≈ 11.4
10.48 + 6 = 16.48 ≈ 16
Multiplicación y división
Cuando se multiplican varias cantidades, el número de cifras significativas en la respuesta final
es el mismo que el número de cifras significativas en la cantidad que tiene el número más pequeño
de cifras significativas. La misma regla aplica para la división. Ejemplos:
5.65 × 4.4 = 24.86 ≈ 25
5.000 × 1.86 = 9.3 = 9.30
Observar que en el ultimo ejemplo la respuesta correcta es la que tiene 3 cifras significativas, es
decir, el 9.30. A pesar de que 9.3 y 9.30 expresan la misma cantidad una de ellas es mas confiable
que la otra.
Precisión y Exactitud
La precisión de una medida es que tan cerca están las medidas entre si. Esta es una medida de
dispersión, usualmente se expresa mediante la desviación estándar, y solo depende del conjunto de
mediciones. Si se tienen varios valores para la misma medida pero están muy alejados entre si, o en
otras palabras, dispersos, y por ende mayor incertidumbre, se dice que la medida es menos precisa .
La exactitud de una medida es la proximidad que existe entre el valor medido y el valor verdadero
de una medida. Este parámetro esta directamente relacionado con el error de una medida. Entre
mas pequeño es el error se dice que la medida es mas exacta.
3

Práctica 2
FS415
Presentación de Resultados
El resultado de una medición se expresa de la siguiente manera:
x =< x > ±∆x (1)
Donde < x > es el valor central de la medición y ∆x es la incertidumbre absoluta. La incertidumbre
absoluta es la cantidad que determina los limites del intervalo de valores donde confiamos que se
encuentra el valor real de la medida. Es una medida de dispersión de los datos. Como ejemplo:
g = (9.74 ± 0.06)
m
s2
La incertidumbre absoluta debe tener una sola cifra significativa. Ejemplos:
0.0053 → 0.005
0.0055 → 0.006
24.56 → 20
270.60 → 300
En los dos últimos ejemplos se hace una estimación de orden del numero para que posea una sola
cifra significativa. Es decir, llevarlo a un valor entero que puede ser mayor o menor dependiendo
del numero.
El valor central se debe ajustar al numero de decimales que posea la incertidumbre absoluta.
En el caso de que no tenga decimales la incertidumbre se deberá de ajustar el valor central al
orden de magnitud respecto a la ubicación de la cifra significativa de la incertidumbre absoluta.
Ejemplos:
La incertidumbre absoluta es de 0.005 el valor central es de 45.62342. Ya que la incertidumbre
absoluta tiene 3 decimales el valor central tambien tiene que tener este numero de decimales.
Entonces se redondea el valor central a 45.623 y la medida queda expresada como
45.623 ± 0.005
Se tiene una incertidumbre absoluta de 60 y un valor central de 364.4645 como la incerti-
dumbre absoluta es del orden de las decenas el valor central se redondea a este mismo orden.
Por lo tanto se redondea 364.4645 al orden de las decenas, que es 360. La medida queda
expresada como:
360 ± 60
4

Práctica 2
FS415
Mediciones directas
Cuando se hacen varias mediciones directas el valor central de estas mediciones esta dado por
la formula:
< z >=
1
n
X
zi (2)
De la misma manera, cuando se tienen varias mediciones directas la incertidumbre absoluta es
la desviación estándar y su formula es:
∆z =
rP
(zi− < z >)2
n − 1
(3)
Donde:
zi → Cada una de las medidas
n → El numero de medidas
Mediciones indirectas
Para una medición indirecta presentada como:
q =< q > ±∆q
El valor central, < q >, de la medición indirecta se calcula haciendo uso de los valores cen-
trales de cada una de las medidas directas en la ecuación matemática para dicha medición indirecta.
Propagación de errores es el hecho de que las incertidumbres de las medidas directas origina-
les se transfieran a cualquier medida indirecta que las involucre. El método diferencial es utilizado
para calcular la incertidumbre absoluta de una medición indirecta:
∆q =
s
∂q
∂z1
∆z1
2
+

∂q
∂z2
∆z2
2
+ . . . +

∂q
∂z3
∆z3
2
(4)
Incertidumbre Relativa y Porcentual
La incertidumbre se define como un parámetro no negativo que caracteriza la dispersión de los
valores atribuidos a una medida, esta no debe confundirse con el error de una medida. El valor de
la incertidumbre relativa nos indica la precision de nuestro montaje o medición. La formula para
calcular la incertidumbre relativa es:
Ir =
∆x
x
La incertidumbre porcentual simplemente es la incertidumbre relativa multiplicada por 100:
Ip = Ir × 100 =
∆x
x
× 100
5

Práctica 2
FS415
Error Absoluto, Relativo y Porcentual
El error de una medida es la diferencia entre un valor medido de una magnitud y un valor
de referencia (valor convencional o valor verdadero). El error absoluto se puede encontrar de la
siguiente manera:
EA = |Vr − Vm|
El error relativo es el cociente entre el error absoluto y el valor real:
ER =
|EA|
|Vr|
=
|Vr − Vm|
|Vr|
Donde:
Vr → Valor real
Vm → Valor medido
El error porcentual simplemente es el error relativo multiplicado por 100:
EP = ER × 100 =
|Vr − Vm|
|Vr|
× 100
6

Práctica 2
FS415
Gráficos
Los gráficos ofrecen una representación visual que modela el comportamiento de una variable
en relación con otra y pueden ser utilizados para:
1. Presentar resultados.
2. Analizar la relación entre variables.
3. Estimar pares de datos diferentes a los graficados.
4. Detectar puntos críticos y tendencias.
5. Monitorear procesos y sistemas.
Variables Independientes y Dependientes
Para analizar comportamientos en algún estudio o experimento se debe de considerar cómo al
variar un factor en un sistema afectará a otro factor, por lo que es necesario establecer cuál variable
es la conocida y puede ser controlada para poder analizar cómo es afectado el sistema.
La variable independiente es aquella que se manipula en un estudio con el fin de observar
su efecto sobre otra variable, y es tomada como el factor sobre el que el investigador tiene control
y que se establece antes de que comience el experimento.
La variable dependiente es aquella que se espera que sea afectada o influenciada por la
variación de la variable independiente en un estudio. La variable dependiente es la que se mide,
registra o evalúa constantemente para determinar si hay cambios o diferencias en respuesta a la
manipulación de la variable independiente.
Por ejemplo: En el experimento de un resorte oscilando, se hacen variaciones a la masa (m) de
los pesos agregados a la punta del resorte y se investiga el efecto que esto tiene sobre el periodo
(T). Una forma de expresar este concepto de relación entre estas dos variables (m, T) es mediante
la siguiente expresión:
T = f(m)
Esta nomenclatura indica que el periodo es una función de la masa colgante, en otras palabras,
que el periodo variará según se agregue o quite masa al sistema. Así queda mas evidente que la
variable m es la variable independiente y la variable T es la variable dependiente.
Partes de un Gráfico
El gráfico debe de contener las siguientes partes claves para entenderse en su totalidad:
a. Denominación de los ejes (nombre y unidades según el Sistema Internacional) con respecto a
las variables dependientes e independientes.
7

Práctica 2
FS415
b. Escala del sistema de coordenadas.
c. Enumeración y nombre completo del gráfico.
d. Tabla de datos de la creación del gráfico.
Ecuaciones Empíricas
Una ecuación empírica es una fórmula matemática que se deriva a partir de observaciones o
datos empíricos. A diferencia de las ecuaciones teóricas, las ecuaciones empíricas no se basan en
principios fundamentales o leyes científicas, sino en relaciones observadas en la práctica. Estas
ecuaciones son utilizadas para describir o predecir el comportamiento de un fenómeno o proce-
so, pero no tienen un respaldo teórico sólido. Es importante tener en cuenta que las ecuaciones
empíricas pueden tener limitaciones y su aplicabilidad puede estar restringida al rango de datos
utilizados para su derivación.
El ajuste de una curva se refiere al proceso de encontrar una función matemática (ecuación
empírica) que se ajuste de manera óptima a un conjunto de puntos de datos en un gráfico. El
objetivo de este proceso es encontrar una curva que represente de manera precisa la tendencia y
relación entre los datos observados. Existen diferentes métodos de ajuste de curvas, como el ajuste
lineal, polinomial o exponencial, entre otros. Estos métodos buscan minimizar la discrepancia entre
los valores reales y los valores estimados por la curva ajustada.
El método de ajuste lineal es en el cual nos enfocaremos, este hace referencia a que los datos
trazados en un papel gráfico rectangular dan por resultado una línea recta, la variable y es lineal
respecto a x, por lo que la ecuación que representa la tendencia de los datos sería de la forma:
y = mx + b donde
m → pendiente de la recta
b → intersección en el eje y
(5)
Linealización de Gráficos: Método de Cambio de Variable
Cuando los gráficos no presentan una tendencia lineal directa entre sus variables, se deben de
aplicar operaciones matemáticas a las ecuaciones para relacionar de una nueva manera las variables
dependientes e independientes con el objetivo de buscar que los datos originales logren una relación
lineal.
Método del Cambio de Variable
Las curvas de varios grados de complejidad son el resultado de que y = f(x) no es lineal. Algunas
de estas curvas (parábolas, hipérbolas, curvas simples senoidales, etc) son fácilmente identificables,
pero las mas complejas son muy difíciles de analizar.
El método de cambio de variable es útil cuando se desea linealizar relaciones no lineales en
gráficos y facilita el análisis de los datos y la extrapolación o interpolación, este método consiste
8

Práctica 2
FS415
en aplicar una transformación matemática a los datos originales para obtener una relación lineal
entre las variables.
Si en una gráfica el trazo directo de datos y = f(x) se asemeja a una parábola que tiene la
forma y = kx2
se puede comprobar la suposición haciendo un cambio de variables. Si se traza y
en función de x2
y resulta una linea recta, entonces la suposición original es correcta. Si no resulta
una linea recta, entonces el problema es mas difícil.
Muchas ecuaciones no lineales se pueden transformar en lineales al cambiar las variables con
las cuales se gráfica. Esto se demostrara con algunos ejemplos:
Ejemplos:
1 2 3 4 5
0
10
20
30
40
y
x
0 5 10 15
0
10
20
30
40
y
x2
Figura 1: La gráfica A representa una ecuación de tipo y = kx2
. La gráfica B es el trazo de
y = f(x2
) de donde se puede encontrar la constante (k = 4) a partir de la pendiente. La ecuación
final (empírica) será y = 4x2
.
9

Práctica 2
FS415
0 3 6 9
0
1
2
3
4
5
6 y
x
0 5 10
0
10
20
30
40 y2
x
Figura 2: La gráfica A representa una ecuación y2
= cx. La gráfica B es una trazo de y2
= f(x)
de donde la constante (c = 4) se puede encontrar a partir de la pendiente real. La ecuación final
(empírica) será y2
= 4x.
0 3 6 9
10
20
30
40
y
x
0 5 10
0
10
20
30
40
y
x−1
Figura 3: La gráfica A representa una ecuación supuesta de la forma y = c
x
. La gráfica B es el
trazado de y = f(x−1
), de donde la constante (c = 8) se puede encontrar a partir de la pendiente
real. La ecuación final (empírica) será y = 8
x
Las figuras 4, 5 y 6 simplemente indican una técnica. En cada caso la ecuación empírica final
deberá “ensamblar” exactamente con la original. En la práctica, la ecuación final solo se adapta
10

Práctica 2
FS415
dentro del intervalo que se encuentran los puntos experimentales.
Regresión Lineal: Método de los Mínimos Cuadrados
Como podemos observar en el gráfico ?? del Ejemplo 3, hay puntos que no estén encima de la
función trazada, esto es debido que la ecuación teórica representa una tendencia lineal, pero los
datos experimentales tienen su incertidumbre creando este tipo de discrepancias. Debido a esto,
es necesario aplicar regresión lineal para minimizar las incertidumbres y discrepancias para poder
garantizar precisión al momento de modelar matemáticamente un fenómeno físico.
Definición: De todas las curvas que se aproximan a un conjunto dado de puntos, a la curva
que tiene la propiedad de que D2
1 +D2
2 +. . .+D2
n sea la mínima se le llama curva de mejor ajuste.
(Estadística, Murray-Spiegel, 4ta
ed)
yi
f(xi)
xi
f(x) = mx + b
Figura 4: Gráfica que muestra los datos experimentales (en rojo) y la recta de regresión, f(x) =
mx + b.
Cuando la curva que se quiere ajustar es una recta de la forma y = mx + b las ecuaciones para
obtener las constantes m y b son:
m =
N
P
xiyi −
P
xi
P
yi
N
P
x2
i − (
P
xi)2
(6)
b =
P
x2
i
P
yi −
P
xi
P
xiyi
N
P
x2
i − (
P
xi)2
(7)
11

Práctica 2
FS415
Y las respectivas incertidumbres, primero se calcula el factor Sy, definido por:
Sy =
s
P
[f(xi) − yi]2
N − 2
(8)
Luego los errores de la ecuación encontrada están dados por las siguientes ecuaciones:
∆m = Sy
s
N
N
P
x2
i − (
P
xi)2
∆b = Sy
s P
x2
i
N
P
x2
i − (
P
xi)2
(9)
Donde:
m → representa la pendiente del gráfico
b → representa el intercepto del gráfico
N → es el número de observaciones tomadas en el laboratorio
P
xi = x1 + x2 + x3 + . . . + xn
P
xiyi = x1y1 + x2y2 + x3y3 + . . . + xnyn
P
x2
i = x2
1 + x2
2 + x2
3 + . . . + x2
n
(
P
xi)2
= (x1 + x2 + x3 + . . . + xn)2
f(xi) = mxi + b
P
[f(xi) − yi]2
= [f(x1) − y1]2
+ [f(x2) − y2]2
+ ... + [f(xn) − yn]2
Ajuste de Datos en Mathematica
Para encontrar la ecuación empírica ajustada con regresión lineal de un conjunto de datos
de tendencia lineal en Mathematica se utiliza el comando LinearModelFit[x,a], y para
tener las tablas de las incertidumbres de la pendiente e intercepto se utiliza el comando
ParameterTable.
Hay relaciones entre variables independientes y dependientes que no son lineales y en las
cuales no se puede aplicar un método matemático para hacer un ajuste lineal. En estos
casos, se aplica un ajuste de datos no lineal a los datos en cuestión para modelar los datos
en base a una función específica. El proceso para llevar a cabo este tipo de ajuste de datos
en Mathematica es usando el comando NonLinearModelFit.
12

Práctica 2
FS415
Ejemplos
Ejemplo 1
Considere las siguientes mediciones tomadas en un laboratorio con una regla. Expresar las
mediciones de la forma L = L ±∆L
n L
1 12.32
2 12.35
3 12.34
4 12.38
5 12.36
Tabla 1: Mediciones con regla
Solución: Como primer paso se calcula el valor central de la medida haciendo uso de la media
aritmética.
L =
12.32 + 12.35 + 12.34 + 12.38 + 12.36
5
= 12.35
El segundo paso es calcular la incertidumbre absoluta haciendo uso de la desviación estándar.
∆L =
r
(12.32 − 12.35)2 + (12.35 − 12.35)2 + (12.34 − 12.35)2 + (12.38 − 12.35)2 + (12.36 − 12.35)2
5 − 1
∆L =
r
(−0.03)2 + (0)2 + (−0.01)2 + (0.03)2 + (0.01)2
4
= 0.02236 ≈ 0.02
Obteniéndose así el resultado final:
L = 12.35 ± 0.02
Notese que el valor de la incertidumbre absoluta fue redondeado para solo dejarle una cifra
significativa y así cumplir con la regla.
Ejemplo 2
El volumen de un cilindro hueco puede calcularse mediante la siguiente expresión:
V =
π
4
h(D2
− d2
)
Si h, d, y D se han medido de tal forma que:
h = (12.1 ± 0.3)cm
D = (5.3 ± 0.6)cm
13

Práctica 2
FS415
d = (2.8 ± 0.1)cm
Calcule:
a. El volumen del cilindro y expresarlo de la forma V = V ±∆V . Utilizar el método diferencial.
b. La incertidumbre relativa y porcentual del volumen calculado usando el método diferencial.
Solución
a. El volumen del cilindro utilizando el método diferencial
Como el problema pide que se exprese la respuesta de la forma V = V ±∆V este ejercicio
tiene dos componentes. Primero se debe encontrar el valor central, V . Y luego, encontrar
la incertidumbre absoluta, ∆V .
Para encontrar el valor central lo único que se tiene que hacer es evaluar la formula para el
volumen del cilindro usando los valores centrales de las mediciones. Es decir, utilizando h ,
d , D .
Por lo tanto se evalúa:
V =
π
4
h(D2
− d2
)
Donde:
h = 12.1
D = 5.3
d = 2.8
V =
π
4
(12.1)(5.32
− 2.82
) = 192.4422 cm3
Ahora se calcula la incertidumbre absoluta ∆V utilizando el método de derivadas parciales. Ya
que la ecuación tiene solamente tres términos h, D, y d se deriva con respecto a estas variables.
También se sabe que se esta calculando la incertidumbre absoluta del volumen por lo tanto
cambiamos q por V . Se reescribe la formula como:
∆V =
s
∂V
∂h
∆h
2
+

∂V
∂D
∆D
2
+

∂V
∂d
∆d
2
Los términos ∂V
∂h
, ∂V
∂D
, ∂V
∂d
son derivadas parciales y se pueden tomar como una derivada normal,
se trata como constante todo excepto el termino respecto al cual se esta derivando. Se encuentra
la derivada parcial del volumen con respecto a cada una de las variables.
∂V
∂h
=
∂
∂h
π
4
h(D2
− d2
)

=
π
4
(D2
− d2
)
∂V
∂D
=
∂
∂D
π
4
h(D2
− d2
)

=
π
2
hD
14

Práctica 2
FS415
∂V
∂d
=
∂
∂d
π
4
h(D2
− d2
)

= −
π
2
hd
Se sustituyen las derivadas en la formula para la incertidumbre absoluta:
∆V =
rπ
4
(D2 − d2)(∆h)
2
+
π
2
hD(∆D)
2
+

−
π
2
hd(∆d)
2
Los valores de h, D, y d son simplemente los valores centrales de cada una de las mediciones
y los valores de ∆h, ∆D, y ∆d son la incertidumbre absoluta de cada medición. Entonces se
sustituyen los valores en la ecuación:
∆V =
rπ
4
(5.32 − 2.82)(0.3)
2
+
π
2
× 12.1 × 5.3(0.6)
2
+

−
π
2
× 12.1 × 2.8(0.1)
2
= 60.8622 cm3
Ahora ya se tiene el valor central y la incertidumbre absoluta de la medida, lo único que resta es
expresarla con la cantidad de cifras significativas correcta. La incertidumbre absoluta se escribe
con una sola cifra significativa, ya que ∆V tiene mas de una cifra significativa se tiene que
reducir el numero de cifras significativas que esta tiene. Para representar el numero 60.8622 con
una cifra significativa se tiene que expresar como 60.
El valor central se debe ajustar de acuerdo al orden de la incertidumbre absoluta. Entonces
tenemos que redondear el valor al orden de las decenas. Por lo tanto nuestro valor central seria
190. El valor del volumen quedaría expresado como:
V = (190 ± 60) cm3
b. La incertidumbre relativa y porcentual del volumen calculado usando el método diferencial.
La incertidumbre relativa simplemente es la incertidumbre absoluta dividida entre el valor
central. El volumen del cilindro es:
V = (190 ± 60) cm3
La incertidumbre absoluta es 60 y el valor central es 190. Consecuentemente la incertidumbre
relativa es:
Ir =
∆V
V
=
60
190
= 0.3158
La incertidumbre porcentual es la incertidumbre absoluta multiplicada por 100. Entonces:
Ip = Ir × 100 = 0.3158 × 100 = 31.58 %
15

Práctica 2
FS415
Ejemplo 3
Se tomaron las siguientes mediciones de laboratorio para un resorte al cual se le fueron colgan-
do masas distintas. Calcule la pendiente y el intercepto para el gráfico L = f(m) por el método
de los mínimos cuadrados, tomando en cuenta que el modelo teórico del sistema esta dado por la
siguiente ecuación:
Lf = Li +
g
k
m
n Masas (gr) Longitud (mm)
1 200 60
2 400 120
3 500 150
4 700 210
5 900 260
6 1000 290
Solución:
i Mi Li M2
i MiLi f(Mi) [f(Mi) − Li]2
1 200 60 40000 12000 62.598 6.7489
2 400 120 160000 48000 119.751 0.0621
3 500 150 250000 75000 148.327 2.7976
4 700 210 490000 147000 205.480 20.4265
5 900 260 810000 234000 262.633 6.9351
6 1000 290 1000000 290000 291.210 1.4640
P
3700 1090 2750000 806000 1090.000 38.4342
Donde Mi representa las masas y Li las longitudes.
m =
6 ∗ 806000 − 3700 ∗ 1090
6 ∗ 2750000 − (3700)2
≈ 0.286 mm/gr
b =
2750000 ∗ 1090 − 3700 ∗ 806000
6 ∗ 2750000 − (3700)2
≈ 5.44 mm
De donde resulta:
y = 0.286x + 5.44
Ahora podemos calcular las incertidumbres:
Sy =
q
38.4342
6−2
= 3.0998
∆m = (3.0998)
r
6
6 ∗ 2750000 − (3700)2
= 0.0045
16

Práctica 2
FS415
∆b = (3.0998)
r
2750000
6 ∗ 2750000 − (3700)2
= 3.0064
Tomando en cuenta las cifras significativas, la presentación de estos datos seria:
m = (0.286 ± 0.005)
mm
gr
b = (5 ± 3) mm
17

Práctica 2
FS415
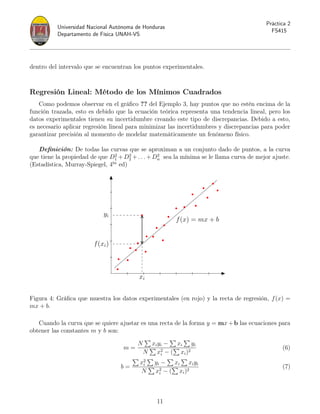
Cálculo y Análisis de Resultados
Proceso Completo de Regresión Lineal
Se sabe que los datos mostrados en la en la Tabla 3 cumplen la relación y = mxn
+ b.
Tabla 2: Tabla de Datos del Ejercicio 1
x 0.7 4 25 100 300 800
y 0.71 1.00 1.75 3.00 4.83 7.57
Hacer los siguientes incisos usando el software Mathematica. Tomar en cuenta las partes
de un gráfico explicadas en el manual para los gráficos en donde se utilizan el comando Show:
1. Gráficar los datos de tabla 2 usando el comando ListPlot.
2. Graficar y = f(x0.25
), y = f(x0.5
), y = f(x−1
) usando el comando ListPlot
3. ¿Cuál de los gráficos anteriores resulto ser lineal y cual es el valor de n?
4. Aplicar regresión lineal a los datos linealizados identificados en el inciso 3 utilizando el co-
mando LinearModelFit[x,a] y obtener las incertidumbres de la pendiente e intercepto
utilizando el comando ParameterTable. Recuerde presentar la pendiente e incertidumbre
de la siguiente manera (m = m ±∆m) y (b = b ±∆b) respectivamente.
5. Graficar la ecuación de la regresión lineal utilizando el comando Plot.
6. Utilizar el comando Show para superponer el gráfico identificado en el inciso 3 y el gráfico
del inciso 5.
7. Escribir la ecuación empírica.
8. Graficar la ecuación empírica utilizando el comando Plot.
9. Utilizar el comando Show para superponer los gráficos del inciso 1 y el gráfico del inciso 8.
10. Calcular la incertidumbre porcentual de los datos de la pendiente y del intercepto.
Ajuste de Datos No Lineales y Propagación de Errores
Se hicieron las siguientes mediciones del campo de inducción magnética en el eje axial de una
bobina. La relación entre el campo inducción magnética, (B), y la ubicación de un punto z sobre
el eje axial esta dado por la siguiente ecuación:
B =
C
(R2 + z2)3/2
18

Práctica 2
FS415
z (m) B (T)
-15 1.7450
-12 4.3896
-9 11.7605
-6 31.2185
-3 68.5871
0 94.0838
3 68.5871
6 31.2185
9 11.7605
12 4.3896
Tabla 3: Tabla de Datos del Ejercicio 2
Hacer los siguientes incisos usando el software Mathematica. Tomar en cuenta las partes
esenciales de gráficos explicadas en el manual solo en los gráficos donde se utilizan el comando
Show:
1. Gráficar de los datos de tabla 3 usando el comando ListPlot.
2. Determinar el valor central de R y C usando el comando NonlinearModelFit
3. Determinar la incertidumbre absoluta de R y C usando el comando ParameterTable.
4. Expresar las constantes R y C de la siguiente forma: R = R ±∆R y C = C ±∆C.
5. Graficar el campo de inducción magnética como función de la posición en el eje axial B = f(z)
en el dominio de -15 hasta 15, tomando en cuenta el valor central de R y C del inciso anterior,
usando el comando Plot.
6. Utilizar el comando Show para superponer los gráficos del paso 1 y 5.
7. Calcular el valor central de B en el punto z = 10m, tomando en cuenta los valores de C y R
del inciso 6.
8. Calcular la incertidumbre absoluta de B mediante propagación de errores en el punto espe-
cificado en el inciso anterior, tomando en cuenta una ∆z = 0.1m y los valores de C y de R
del inciso 6.
9. Expresar el valor de la constante B de la siguiente forma: B = B ±∆B.
19

02__Repaso_de_Tratamiento_de_Errores_y_Ajuste_de_Datos.pdf

Más contenido relacionado

Similar a 02__Repaso_de_Tratamiento_de_Errores_y_Ajuste_de_Datos.pdf

Último

02__Repaso_de_Tratamiento_de_Errores_y_Ajuste_de_Datos.pdf