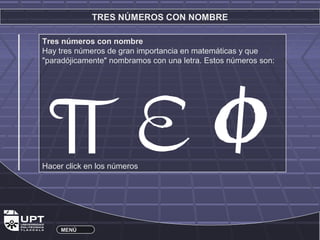
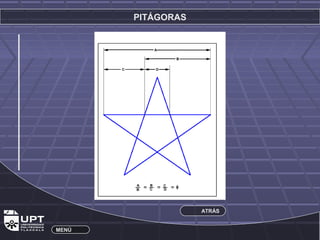
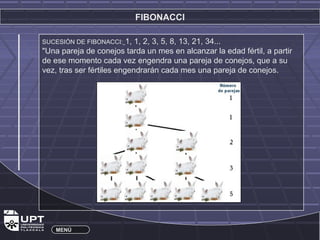
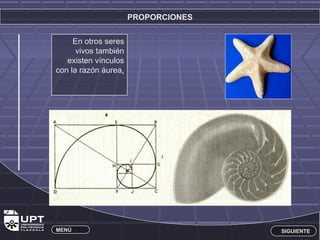
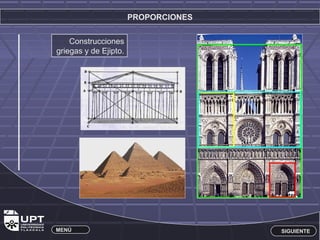
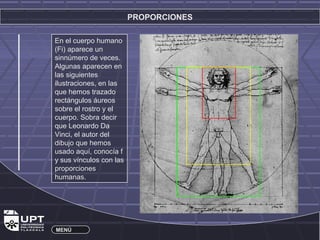
Este documento resume la historia y aplicaciones de varios números importantes como los irracionales, π, e, y el número de oro φ. Explica el origen de los números irracionales en la antigua Grecia y cómo figuras como Pitágoras y Fibonacci contribuyeron a su estudio. También describe cómo el número de oro φ se encuentra en proporciones estéticas como en el cuerpo humano y obras de arte.

2. Dr. Víctor Cabrera Peláez
Ingeniería Química Grupo B
Montiel Rivera Sujaily
Fuentes Salado Víctor Joaquín
Navarro Rosete Jezabel Iraí
Telpalo Méndez Yuri
Ingeniería Mecatrónica Grupo B
Zepeda Sánchez Giovanni
Chávez Cervantes Raúl Abdel
Barragán Martínez Roberto

3. ORIGEN
NÚMEROS
PITÁGORAS
FIBONACCI
NÚMERO DORADO
RECTÁNGULO
PRPORCIONES
CONCLUSIONES

4. ORIGEN
El origen de los números irracionales
Los números irracionales aparecen en la historia de la
matemática vinculados a la geometría.
La matemática pitagórica estaba basada en los enteros
positivos y en todo lo que es expresable en términos de
operaciones entre ellos, por lo tanto a lo más se llegaron a
considerar fracciones positivas y se encontraron con que estas
cantidades no eran números enteros ni fracciones.
A estos números, que no eran ni enteros ni fracciones, los
llamaron alogos o irracionales. En la época de Platón (428 -
347 A.C.) ya se conocía la irracionalidad de los números:
MENÚ

5. TRES NÚMEROS CON NOMBRE
Tres números con nombre
Hay tres números de gran importancia en matemáticas y que
"paradójicamente" nombramos con una letra. Estos números son:
Hacer click en los números
MENÚ

6. TRES NÚMEROS CON NOMBRE
Tres números con nombre
El número designado con la letra griega = 3,14159....(Pi) que relaciona la
longitud de la circunferencia con su diámetro ( Longitud = 2..radio= .diámetro).
El número e = 2´71828......, inicial del apellido de su descubridor Leonhard
Euler (matemático suizo del siglo XVIII) que aparece como límite de la
sucesión de término general .
El número designado con letra griega = 1,61803... (Fi), llamado número de oro
y que es la inicial del nombre del escultor griego Fidias que lo tuvo presente en
sus obras.
MENÚ

7. PITÁGORAS
Pitágoras (c. 582-c. 500 a.C.), filósofo y matemático griego
La estrella pentagonal o pentágono estrellado
era, según la tradición, el símbolo de los
seguidores de Pitágoras. Los pitagóricos
pensaban que el mundo estaba configurado
según un orden numérico, donde sólo tenían
cabida los números fraccionarios.
La casualidad hizo que en su propio símbolo se
encontrara un número raro: el numero de oro.
MENÚ
SIGUIENTE

8. PITÁGORAS
MENÚ
ATRÁS

9. FIBONACCI
SUCESIÓN DE FIBONACCI: 1, 1, 2, 3, 5, 8, 13, 21, 34...
"Una pareja de conejos tarda un mes en alcanzar la edad fértil, a partir
de ese momento cada vez engendra una pareja de conejos, que a su
vez, tras ser fértiles engendrarán cada mes una pareja de conejos.
MENÚ

10. LA SECCIÓN ÁUREA Y EL NÚMERO DE ORO
La sección áurea es la división de un segmento en dos partes, una en
menor y otra en mayor tamaño. Es decir, que el segmento menor es
proporcional al segmento mayor y viceversa.
De esta manera se establece una relación de tamaños con la misma
proporcionalidad entre el todo dividido en mayor y menor.
Esta proporción o forma de seleccionar proporcionalmente una línea se
llama proporción áurea.Tomemos un segmento de longitud uno y
hagamos en el la división indicada anteriormente
MENÚ
SIGUIENTE

11. LA SECCIÓN ÁUREA Y EL NÚMERO DE ORO
Aplicando la proporción áurea obtenemos la siguiente
ecuación que tendremos que resolver
X - 1
X
= X11 - X = X2 X + X - 1= 0 2
ANTERIOR
MENÚ

12. EL RECTÁNGULO ÁUREO
Dibujamos un cuadrado y marcamos el punto medio de uno de sus
lados. Lo unimos con uno de los vértices del lado opuesto y llevamos
esa distancia sobre el lado inicial, de esta manera obtenemos el lado
mayor del rectángulo.
MENÚ

13. PROPORCIONES
El cuadro de Dalí
Leda atómica,
pintado en 1949,
sintetiza siglos de
tradición
matemática y
simbólica,
especialmente
pitagórica.
MENÚ SIGUIENTE

14. PROPORCIONES
En otros seres
vivos también
existen vínculos
con la razón áurea.
MENÚ SIGUIENTE

15. PROPORCIONES
Construcciones
griegas y de Ejipto.
MENÚ SIGUIENTE

16. PROPORCIONES
En el cuerpo humano
(Fi) aparece un
sinnúmero de veces.
Algunas aparecen en
las siguientes
ilustraciones, en las
que hemos trazado
rectángulos áureos
sobre el rostro y el
cuerpo. Sobra decir
que Leonardo Da
Vinci, el autor del
dibujo que hemos
usado aquí, conocía f
y sus vínculos con las
proporciones
humanas.
MENÚ

17. CONCLUSIONES
Entre los números reales encontramos que se descubrieron unos
números llamados irracionales, lo cual fue un avance muy importante en
las matemáticas de esa época, debido a esto la geometría tuvo cambios
contrastantes en sus planteamientos, como fue mencionado en el inicio
de este documento, se tenía la idea que la figuras geométricas estaban
formadas por el seguimiento de puntos finitos, hasta que encontraron
que estas también estaban formadas por números irracionales. Entre
estos fi.
El número dorado también llamado número divino lo encontramos en las
formas geométricas de la naturaleza, parase ser que estamos diseñados
bajo un mismo patrón numérico de proporcionalidad, ya que
multiplicando este número (0.618) por las magnitudes de ciertos objetos
y hasta de nuestro cuerpo nos damos cuenta que estamos formados
bajo este patrón de proporción.
MENÚ