Este documento presenta información sobre el cálculo del área bajo una curva y la longitud de arcos de curva utilizando integrales. Explica cómo usar la integral definida para calcular el área entre dos funciones o entre una función y una línea. También muestra ejemplos numéricos de cómo calcular estas áreas y longitudes. Finalmente, proporciona detalles sobre dividir regiones entre funciones en subintervalos para facilitar el cálculo cuando las funciones cambian de orden.

2. ÍNDICE
1. Unidad 3: Aplicación de la integral 3
1.1 Objetivo 3
1.2 Introducción 3
2. Información de los subtemas 4
2.1 Área de figuras planas 4
2.2 Longitud de curvas planas 23
3. Recursos complementarios 29
4. Bibliografía 30

3. Aplicación de la integral – Integral de área e integral de longitud
3
©
Universidad
Estatal
de
Milagro
–
UNEMI
1. Unidad 3:
» Objetivo:
Utilizar el cálculo integral para encontrar áreas de figuras planas formadas por curvas
definidas por funciones; además, usar las técnicas de integración y su definición para
encontrar la longitud de arcos de curvas expresadas matemáticamente a lo largo de un
plano.
» Introducción:
Las técnicas de integración sirven para muchas aplicaciones, una de las más
fundamentales y básicas es encontrar el área bajo una curva expresada como una
función 𝑦 = 𝑓(𝑥) o 𝑥 = 𝑔(𝑦). Además de permitir encontrar regiones bajo una función
cualquiera, también nos permite calcular la superficie o área que existe entre dos curvas
o rectas no poligonales. Otras de las aplicaciones de las integrales estudiadas en este
compendio es la de encontrar la longitud de un arco de curva definida dentro de un
intervalo. Estas aplicaciones son de gran importancia ya que resulta complejo calcular el
área o longitud de curvas con las matemáticas básicas, la rapidez y sencillez que nos
proporcionan las integrales en esta temática de su mayor importancia.

4. Aplicación de la integral – Integral de área e integral de longitud
4
©
Universidad
Estatal
de
Milagro
–
UNEMI
2. Información de los subtemas
2.1 Área de figuras planas
Como ya se ha estudiado en temas anteriores, la integral definida es importante para
calcular áreas bajo una curva definida por funciones. Ahora bien, se analizará el método
adecuado para calcular áreas entre dos funciones; para aquello observemos la siguiente
gráfica:
Se puede observar una región sombreada a la cual se la ha denominado 𝑆; la misma que
está limitada por dos funciones 𝑓(𝑥) y 𝑔(𝑥), también por dos rectas verticales 𝑥 = 𝑎 y
𝑥 = 𝑏. Además, debemos tener en cuenta ciertas características de estas funciones:
» Las funciones 𝑓 y 𝑔 son continuas en el intervalo [𝑎, 𝑏]
» la función 𝑓(𝑥) es mayor igual que la función 𝑔(𝑥), es decir, 𝑓(𝑥) ≥ 𝑔(𝑥) en el
intervalo cerrado [𝑎, 𝑏]
Para obtener el área 𝑆 de la figura formada por las funciones 𝑓(𝑥) y 𝑔(𝑥) procedemos
a dividir la región 𝑆 en 𝑛 números de rectángulos con igual anchura (de la misma manera
que se explicó en el tema 1 de la unidad 1). Se tendrá algo similar a la siguiente figura:
Figura 1. Área de una figura plana
Fuente: (Stewart, 2012)

5. Aplicación de la integral – Integral de área e integral de longitud
5
©
Universidad
Estatal
de
Milagro
–
UNEMI
Analizando la figura, aislando un rectángulo cualquiera tendremos:
Donde:
» Base del rectángulo: ∆𝑥
» Altura del rectángulo: 𝑓(𝑥1) − 𝑔(𝑥1)
Según el análisis anterior y aplicada la suma de Riemann, obtendremos:
3[𝑓(𝑥1) − 𝑔(𝑥1)]
4
156
∆𝑥
Figura 2. División en 𝑛 rectángulos de igual anchura
Fuente: (Stewart, 2012)
Figura 3. Rectángulo representativo de la región 𝑆
Fuente: (Stewart, 2012)

6. Aplicación de la integral – Integral de área e integral de longitud
6
©
Universidad
Estatal
de
Milagro
–
UNEMI
Ahora bien, si aumentamos el número de rectángulos mejoramos la aproximación del
resultado (véase compendio unidad 1 tema 1), por lo tanto:
𝐴 = lim
4→<
3[𝑓(𝑥1) − 𝑔(𝑥1)]
4
156
∆𝑥
Áreas de figuras planas: ejemplo 1.
Ejemplo 1: Determinar el área de la región acotada por arriba por 𝑓(𝑥) = 9 −
>?
@
, por
debajo por 𝑔(𝑥) =
>?
@
− 4 y a los lados por 𝑥6 = 0 y 𝑥C = 6.
La región descrita anteriormente se puede observar en el siguiente gráfico:
𝑓(𝑥)
𝑔(𝑥)
Teorema 1: El área 𝐴 de una superficie limitada por dos funciones 𝑓(𝑥) y 𝑔(𝑥), y las
rectas 𝑥 = 𝑎 y 𝑥 = 𝑏; donde se cumple que 𝑓 y 𝑔 son continuas y 𝑓(𝑥) ≥ 𝑔(𝑥) en el
intervalo cerrado [𝑎, 𝑏] es:
𝐴 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥
Figura 4. Gráfica ejemplo 1
Fuente: Elaboración propia

7. Aplicación de la integral – Integral de área e integral de longitud
7
©
Universidad
Estatal
de
Milagro
–
UNEMI
Ahora bien, aplicando el teorema 1:
𝐴 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥
Donde:
𝑓(𝑥) = 9 −
𝑥C
8
𝑔(𝑥) =
𝑥C
8
− 4
𝑎 = 𝑥6 = 0
𝑏 = 𝑥C = 6
Entonces, tendremos:
𝐴 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥 = E JK9 −
𝑥C
8
L − K
𝑥C
8
− 4LM
N
O
𝑑𝑥 = E J9 −
𝑥C
8
−
𝑥C
8
+ 4M
N
O
𝑑𝑥
Aplicando las propiedades de las integrales:
𝐴 = E 9
N
O
𝑑𝑥 − E
𝑥C
8
N
O
𝑑𝑥 − E
𝑥C
8
N
O
𝑑𝑥 + E 4
N
O
𝑑𝑥
𝐴 = 9 E 𝑑𝑥
N
O
−
1
8
E 𝑥C
N
O
𝑑𝑥 −
1
8
E 𝑥C
N
O
𝑑𝑥 + 4 E 𝑑𝑥
N
O
Integrando:
𝐴 = J9𝑥 −
1
8
∙
𝑥S
3
−
1
8
∙
𝑥S
3
+ 4𝑥M
O
N
𝐴 = J9𝑥 −
𝑥S
24
−
𝑥S
24
+ 4𝑥M
O
N
= J9𝑥 −
2𝑥S
24
+ 4𝑥M
O
N
= J9𝑥 −
𝑥S
12
+ 4𝑥M
O
N
𝐴 = J9(6) −
(6)S
12
+ 4(6)M − J9(0) −
(0)S
12
+ 4(0)M

8. Aplicación de la integral – Integral de área e integral de longitud
8
©
Universidad
Estatal
de
Milagro
–
UNEMI
𝐴 = V54 −
216
12
+ 24X − (0) = 54 −
216
12
+ 24
𝐴 = 54 − 18 + 24 = 60 𝑢C
Existen otros casos en donde las funciones que intervienen 𝑓(𝑥) y 𝑔(𝑥) son positivas
como se muestra en la siguiente figura:
Figura 4. Caso donde 𝑓 y 𝑔 son positivas
Fuente: (Stewart, 2012)
Para el caso mencionado anteriormente se cumple que:
𝐴 = [área bajo 𝑦 = 𝑓(𝑥)] − [área bajo 𝑦 = 𝑔(𝑥)]
Donde podemos comprobar el cumplimiento del teorema 1:
𝐴 = E 𝑓(𝑥)
F
G
𝑑𝑥 − E 𝑔(𝑥)
F
G
𝑑𝑥 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥

9. Aplicación de la integral – Integral de área e integral de longitud
9
©
Universidad
Estatal
de
Milagro
–
UNEMI
Áreas de figuras planas: ejemplo 2.
Ejemplo 2: Determinar el área de la región acotada por arriba por 𝑓(𝑥) = 𝑥, por debajo
por 𝑔(𝑥) = 𝑒>c@
y a los lados por 𝑥6 = 2 y 𝑥C = 8.
Observando la gráfica:
Ahora bien, aplicamos:
𝐴 = E 𝑓(𝑥)
F
G
𝑑𝑥 − E 𝑔(𝑥)
F
G
𝑑𝑥 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥
Donde:
𝑓(𝑥) = 𝑥
𝑔(𝑥) = 𝑒>c@
𝑎 = 𝑥6 = 2
𝑏 = 𝑥C = 8
𝑓(𝑥)
𝑔(𝑥)
Figura 4. Gráfica ejemplo 2
Fuente: Elaboración propia

10. Aplicación de la integral – Integral de área e integral de longitud
10
©
Universidad
Estatal
de
Milagro
–
UNEMI
Entonces, tendremos:
𝐴 = E 𝑓(𝑥)
F
G
𝑑𝑥 − E 𝑔(𝑥)
F
G
𝑑𝑥 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥 = E [𝑥 − 𝑒>c@]
@
C
𝑑𝑥
Aplicando las propiedades de las integrales e integrando:
𝐴 = E [𝑥 − 𝑒>c@]
@
C
𝑑𝑥 = E 𝑥
@
C
𝑑𝑥 − E 𝑒>c@
@
C
𝑑𝑥 = J
𝑥C
2
− 𝑒>c@
M
C
@
𝐴 = J
(8)C
2
− 𝑒@c@
M − J
(2)C
2
− 𝑒Cc@
M = d
64
2
− 𝑒O
e − d
4
2
− 𝑒cN
e
𝐴 = [32 − 1] − [2 − 𝑒cN] = 31 − 2 + 𝑒cN
= (29 + 𝑒cN
) 𝑢C
Podemos encontrarnos con la situación descrita a continuación: supongamos que se
debe calcular el área entre dos funciones 𝑓(𝑥) y 𝑔(𝑥), en la cual se cumple que 𝑓(𝑥) ≥
𝑔(𝑥) en el intervalo [𝑎, 𝑏]; y que 𝑔(𝑥) ≥ 𝑓(𝑥) en el intervalo [𝑏, 𝑐].
Para encontrar el área total debemos dividir la región en varias áreas 𝐴6, 𝐴C, 𝐴S,…, 𝐴4;
después, se procede a realizar la suma de tales áreas para encontrar el total, es decir:
𝐴g = 𝐴6 + 𝐴C + 𝐴S + ⋯ + 𝐴4
Figura 5. Área entre funciones
Fuente: (Stewart, 2012)

11. Aplicación de la integral – Integral de área e integral de longitud
11
©
Universidad
Estatal
de
Milagro
–
UNEMI
Se debe tener en cuenta los siguiente:
» Cuando 𝑓(𝑥) ≥ 𝑔(𝑥) entonces 𝑓(𝑥) − 𝑔(𝑥)
» Cuando 𝑔(𝑥) ≥ 𝑓(𝑥) entonces 𝑔(𝑥) − 𝑓(𝑥)
Por lo tanto, se llega a la siguiente conclusión:
|𝑓(𝑥) − 𝑔(𝑥)| = j
𝑓(𝑥) − 𝑔(𝑥)
𝑔(𝑥) − 𝑓(𝑥)
Teorema 2: El área entre las curvas 𝑦 = 𝑓(𝑥) y 𝑦 = 𝑔(𝑥) y entre 𝑥 = 𝑎 y 𝑥 = 𝑏 es:
𝐴 = E |𝑓(𝑥) − 𝑔(𝑥)|
F
G
𝑑𝑥

12. Aplicación de la integral – Integral de área e integral de longitud
12
©
Universidad
Estatal
de
Milagro
–
UNEMI
Áreas de figuras planas: ejemplo 3.
Ejemplo 3: Determinar el área de la región acotada por 𝑓(𝑥) = 3𝑥S
− 𝑥C
− 10𝑥 y
𝑔(𝑥) = −𝑥C
+ 2𝑥, en el intervalo [−2, 2]
Graficamos las funciones e identificamos la región definida por el intervalo:
Analizando el gráfico, podemos observar que:
» Primer intervalo: [−2, 0]
» Segundo intervalo: [0, 2]
Figura 6. Gráfica ejemplo 3
Fuente: Elaboración propia

13. Aplicación de la integral – Integral de área e integral de longitud
13
©
Universidad
Estatal
de
Milagro
–
UNEMI
Aplicado el teorema 2, tendremos:
𝐴 = E |𝑓(𝑥) − 𝑔(𝑥)|
F
G
𝑑𝑥 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥 + E [𝑔(𝑥) − 𝑓(𝑥)]
F
G
𝑑𝑥
𝐴 = E |(3𝑥S
− 𝑥C
− 10𝑥) − (−𝑥C
+ 2𝑥)|
C
cC
𝑑𝑥
𝐴 = E [(3𝑥S
− 𝑥C
− 10𝑥) − (−𝑥C
+ 2𝑥)]
O
cC
𝑑𝑥 + E [(−𝑥C
+ 2𝑥) − (3𝑥S
− 𝑥C
− 10𝑥)]
C
O
𝑑𝑥
𝐴 = E [3𝑥S
− 𝑥C
− 10𝑥 + 𝑥C
− 2𝑥]
O
cC
𝑑𝑥 + E [−𝑥C
+ 2𝑥 − 3𝑥S
+ 𝑥C
+ 10𝑥]
C
O
𝑑𝑥
𝐴 = E [3𝑥S
− 12𝑥]
O
cC
𝑑𝑥 + E [−3𝑥S
+ 12𝑥]
C
O
𝑑𝑥
Integramos aplicando las propiedades y fórmulas adecuadas:
𝐴 = E [3𝑥S
− 12𝑥]
O
cC
𝑑𝑥 + E [−3𝑥S
+ 12𝑥]
C
O
𝑑𝑥 = J
3𝑥k
4
−
12𝑥C
2
M
cC
O
+ J−
3𝑥k
4
+
12𝑥C
2
M
O
C
𝐴 = J
3𝑥k
4
− 6𝑥C
M
cC
O
+ J−
3𝑥k
4
+ 6𝑥C
M
O
C
𝐴 = J
3(0)k
4
− 6(0)C
M − J
3(−2)k
4
− 6(−2)C
M + J−
3(2)k
4
+ 6(2)C
M − J−
3(0)k
4
+ 6(0)C
M
𝐴 = [0 − 0] − J
3(16)
4
− 6(4)M + J−
3(16)
4
+ 6(4)M − [−0 + 0]
𝐴 = − d
48
4
− 24e + d−
48
4
+ 24e
𝐴 = −[12 − 24] + [−12 + 24] = 12 + 12 = 24 𝑢C

14. Aplicación de la integral – Integral de área e integral de longitud
14
©
Universidad
Estatal
de
Milagro
–
UNEMI
También existe la forma de encontrar áreas entre curvas considerando a 𝑥 como función
de 𝑦, es decir, 𝑥 = 𝑓(𝑦). Por ejemplo:
Podemos observar que tenemos dos funciones 𝑥 = 𝑔(𝑦), 𝑥 = 𝑓(𝑦), donde 𝑓(𝑦) ≥
𝑔(𝑦); además, tenemos las constantes 𝑦 = 𝑑 y 𝑦 = 𝑐, las cuales delimitan el área a
calcular. Para encontrar de manera correcta el área de la región limitada anterior,
utilizaremos el siguiente teorema:
Figura 7. Área entre funciones
Fuente: (Stewart, 2012)
Teorema 3: El área entre las curvas 𝑥 = 𝑓(𝑦) y 𝑥 = 𝑔(𝑦) y entre 𝑦 = 𝑐 y 𝑦 = 𝑑 es:
𝐴 = E [𝑓(𝑦) − 𝑔(𝑦)]
l
m
𝑑𝑦

15. Aplicación de la integral – Integral de área e integral de longitud
15
©
Universidad
Estatal
de
Milagro
–
UNEMI
Áreas de figuras planas: ejemplo 4.
Ejemplo 4: Calcular el área de la región limitada por:
j
𝑦 = 𝑥 − 1
𝑥 = 3 − 𝑦C
En este caso, sería mejor trabajar con 𝑥 en función de 𝑦, es decir, 𝑥 = 𝑓(𝑦). En las
funciones dadas podemos notar que 𝑥 = 3 − 𝑦C
ya está en función de 𝑦; pero la función
𝑦 = 𝑥 − 1 está en función de 𝑥, es a aquella la que hay que hacer el cambio:
𝑦 = 𝑥 − 1
Despejando 𝑥:
𝑥 = 𝑦 + 1
Ahora ya tenemos a las dos funciones con 𝑥 en función de 𝑦:
j
𝑥 = 𝑦 + 1
𝑥 = 3 − 𝑦C
Obteniendo la gráfica:
Figura 8. Área entre funciones
Fuente: (Villena Muñoz)

16. Aplicación de la integral – Integral de área e integral de longitud
16
©
Universidad
Estatal
de
Milagro
–
UNEMI
Podemos observar que las funciones se intersectan en dos puntos, por lo tanto,
necesitamos encontrar esos puntos, los cuales representarán los límites del área
específica. Para ello, igualamos las funciones y despejamos 𝑦:
𝑦 + 1 = 3 − 𝑦C
𝑦C
+ 𝑦 + 1 − 3 = 0
𝑦C
+ 𝑦 − 2 = 0
(𝑦 + 2)(𝑦 − 1) = 0
𝑦 = −2 ∨ 𝑦 = 1
Habiendo encontrado las rectas 𝑦 = 𝑐 = −2 y 𝑦 = 𝑑 = 1 procedemos a utilizar el
teorema propuesto anteriormente:
𝐴 = E [𝑓(𝑦) − 𝑔(𝑦)]
l
m
𝑑𝑦
Reemplazando:
𝐴 = E [(3 − 𝑦C
) − (𝑦 + 1)]
6
cC
𝑑𝑦 = E [3 − 𝑦C
− 𝑦 − 1]
6
cC
𝑑𝑦 = E [−𝑦C
− 𝑦 + 2]
6
cC
𝑑𝑦
𝐴 = E −[𝑦C
+ 𝑦 − 2]
6
cC
𝑑𝑦 = − E 𝑦C
+ 𝑦 − 2
6
cC
𝑑𝑦
Integrando:
𝐴 = − J
𝑦S
3
+
𝑦C
2
− 2𝑦M
cC
6
𝐴 = − oJ
(1)S
3
+
(1)C
2
− 2(1)M − J
(−2)S
3
+
(−2)C
2
− 2(−2)Mp
𝐴 = − jd
1
3
+
1
2
− 2e − d
−8
3
+
4
2
+ 4eq = − d
1
3
+
1
2
− 2 +
8
3
− 2 − 4e
𝐴 = − d
2 + 3 − 12 + 16 − 12 − 24
6
e = − V−
27
6
X =
9
2
𝑢C

17. Aplicación de la integral – Integral de área e integral de longitud
17
©
Universidad
Estatal
de
Milagro
–
UNEMI
Áreas de figuras planas: otros ejemplos.
Ejemplo 5: Calcular el área de la región limitada por:
j
𝑓(𝑥) = 𝑥 + 4
𝑔(𝑥) = 𝑥C
− 2
Realizamos la gráfica de ambas funciones:
Debemos encontrar los puntos donde las gráficas se cruzan; para ello igualamos las
funciones y despejamos 𝑥:
𝑥 + 4 = 𝑥C
− 2
𝑥C
− 𝑥 − 4 − 2 = 0
𝑥C
− 𝑥 − 6 = 0
(𝑥 − 3)(𝑥 + 2) = 0
𝑥 = 3 ∨ 𝑥 = −2
Figura 9. Gráfica ejemplo 5
Fuente: Elaboración propia

18. Aplicación de la integral – Integral de área e integral de longitud
18
©
Universidad
Estatal
de
Milagro
–
UNEMI
Por lo tanto, tendremos como limitantes del área a:
𝑓(𝑥) = 𝑥 + 4
𝑔(𝑥) = 𝑥C
− 2
𝑥6 = 𝑏 = 3
𝑥C = 𝑎 = −2
Aplicando la integral correspondiente:
𝐴 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥 = E [(𝑥 + 4) − (𝑥C
− 2)]
S
cC
𝑑𝑥
𝐴 = E [𝑥 + 4 − 𝑥C
+ 2]
S
cC
𝑑𝑥
Integrando:
𝐴 = J
𝑥C
2
+ 4𝑥 −
𝑥S
3
+ 2𝑥M
cC
S
𝐴 = J
(3)C
2
+ 4(3) −
(3)S
3
+ 2(3)M − J
(−2)C
2
+ 4(−2) −
(−2)S
3
+ 2(−2)M
𝐴 = d
9
2
+ 12 −
27
3
+ 6e − d
4
2
− 8 +
8
3
− 4e = d
9
2
+ 12 − 9 + 6e − d2 − 8 +
8
3
− 4e
𝐴 = d
9
2
+ 9e − d−10 +
8
3
e =
9
2
+ 9 + 10 −
8
3
=
27 + 54 + 60 − 16
6
=
125
6
𝑢C
Ejemplo 6: Calcular el área de la región limitada por:
j
𝑓(𝑥) = 𝑥S − 𝑥C − 6𝑥
𝑔(𝑥) = 0

19. Aplicación de la integral – Integral de área e integral de longitud
19
©
Universidad
Estatal
de
Milagro
–
UNEMI
Graficamos las funciones dadas:
Calculamos los puntos donde las funciones dadas se cruzan:
𝑥S
− 𝑥C
− 6𝑥 = 0
𝑥(𝑥C
− 𝑥 − 6) = 0
𝑥 = 0 ∨ 𝑥C
− 𝑥 − 6 = 0
𝑥 = 0 ∨ (𝑥 − 3)(𝑥 + 2) = 0
𝑥 = 0 ∨ 𝑥 = 3 ∨ 𝑥 = −2
Figura 10. Gráfica ejemplo 6
Fuente: Elaboración propia

20. Aplicación de la integral – Integral de área e integral de longitud
20
©
Universidad
Estatal
de
Milagro
–
UNEMI
Los intervalos son [−2, 0] y [0, 3]. Tenemos:
𝑓(𝑥) = 𝑥S
− 𝑥C
− 6𝑥
𝑔(𝑥) = 0
𝑥6 = 𝑎 = −2
𝑥C = 𝑏 = 0
𝑥S = 𝑐 = 3
Entonces:
𝐴 = E |𝑓(𝑥) − 𝑔(𝑥)|
F
G
𝑑𝑥 = E [𝑓(𝑥) − 𝑔(𝑥)]
F
G
𝑑𝑥 + E [𝑔(𝑥) − 𝑓(𝑥)]
m
F
𝑑𝑥
𝐴 = E [(𝑥S
− 𝑥C
− 6𝑥) − (0)]
O
cC
𝑑𝑥 + E [(0) − (𝑥S
− 𝑥C
− 6𝑥)]
S
O
𝑑𝑥
𝐴 = E [𝑥S
− 𝑥C
− 6𝑥]
O
cC
𝑑𝑥 + E [−𝑥S
+ 𝑥C
+ 6𝑥]
S
O
𝑑𝑥
Integrando:
𝐴 = J
𝑥k
4
−
𝑥S
3
−
6𝑥C
2
M
cC
O
+ J−
𝑥k
4
+
𝑥S
3
+
6𝑥C
2
M
O
S
= J
𝑥k
4
−
𝑥S
3
− 3𝑥C
M
cC
O
+ J−
𝑥k
4
+
𝑥S
3
+ 3𝑥C
M
O
S
𝐴 = J
(0)k
4
−
(0)S
3
− 3(0)C
M − J
(−2)k
4
−
(−2)S
3
− 3(−2)C
M + J−
(3)k
4
+
(3)S
3
+ 3(3)C
M − J−
(0)k
4
+
(0)S
3
+ 3(0)C
M
𝐴 = (0) − J
16
4
−
(−8)
3
− 3(4)M + d−
81
4
+
27
3
+ 3(9)e − (0)
𝐴 = − d4 +
8
3
− 12e + d−
81
4
+ 9 + 27e = −4 −
8
3
+ 12 −
81
4
+ 9 + 27
𝐴 = −4 −
8
3
+ 12 −
81
4
+ 9 + 27 =
−48 − 32 + 144 − 243 + 108 + 324
12
=
253
12
𝑢C

21. Aplicación de la integral – Integral de área e integral de longitud
21
©
Universidad
Estatal
de
Milagro
–
UNEMI
Ejemplo 7: Calcular el área de la región limitada por:
s
𝑓(𝑦) = 𝑦C
𝑔(𝑦) = 6 − 𝑦
𝑦 = 0
Graficamos:
Debemos encontrar el punto donde las gráficas de las funciones se cruzan:
𝑦C
= 6 − 𝑦
𝑦C
+ 𝑦 − 6 = 0
(𝑦 + 3)(𝑦 − 2) = 0
𝑦 = −3 ∨ 𝑦 = 2
Figura 11. Gráfica ejemplo 7
Fuente: Elaboración propia

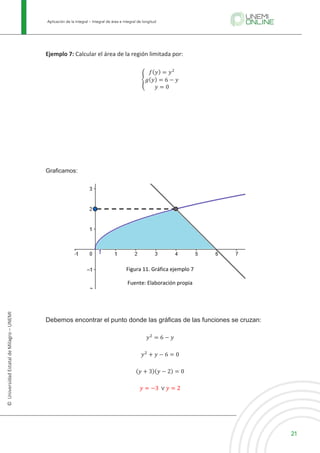
22. Aplicación de la integral – Integral de área e integral de longitud
22
©
Universidad
Estatal
de
Milagro
–
UNEMI
Entonces tendremos:
𝑓(𝑦) = 𝑦C
𝑔(𝑦) = 6 − 𝑦
𝑦 = 𝑐 = 0
𝑦6 = 𝑑 = 2
Para este caso 𝑔(𝑦) ≥ 𝑓(𝑦). Aplicando la integral:
𝐴 = E [𝑓(𝑦) − 𝑔(𝑦)]
l
m
𝑑𝑦 = E [(6 − 𝑦) − (𝑦C
)]
C
O
𝑑𝑦
𝐴 = E [6 − 𝑦 − 𝑦C
]
C
O
𝑑𝑦
Integrando:
𝐴 = J6𝑦 −
𝑦C
2
−
𝑦S
3
M
O
C
𝐴 = J6(2) −
(2)C
2
−
(2)S
3
M − J6(0) −
(0)C
2
−
(0)S
3
M
𝐴 = d12 −
4
2
−
8
3
e − [0] = 12 − 2 −
8
3
=
36 − 6 − 8
3
=
22
3
𝑢C

23. Aplicación de la integral – Integral de área e integral de longitud
23
©
Universidad
Estatal
de
Milagro
–
UNEMI
2.2 Longitud de curvas planas
Usando el cálculo integral también se puede encontrar la longitud de una curva,
utilizando un método similar de aproximaciones, pero en este caso tal aproximación es
poligonal. Para entender de mejor manera lo que se está exponiendo se analizará la
siguiente gráfica:
Tenemos una curva 𝑦 = 𝑓(𝑥), continua en el intervalo [𝑎, 𝑏], el cual ha sido dividido en
𝑛 subintervalos con puntos 𝑥O = 𝑎, 𝑥6, 𝑥C, … , 𝑥1c6, 𝑥1, … , 𝑥4 = 𝑏; todos estos
subintervalos tienen la misma anchura ∆𝑥. Además, los puntos 𝑃O, 𝑃6, 𝑃C,…, 𝑃1c6, 𝑃1,…,
𝑃4; también llamados vértices de la aproximación poligonal; pertenecen a la función 𝑦 =
𝑓(𝑥).
Ahora bien, si calculamos la longitud de las rectas poligonales formadas por los puntos
antes mencionados, tendremos un valor que será una aproximación de la longitud de la
curva. Para tener una mejor exactitud de la longitud que nos interesa, es decir, la de la
curva debemos aumentar el número de subintervalos (esto es similar a las
Figura 12. Longitud de una curva
Fuente: (Stewart, 2012)

24. Aplicación de la integral – Integral de área e integral de longitud
24
©
Universidad
Estatal
de
Milagro
–
UNEMI
aproximaciones por medio de rectángulos, cuando se quería encontrar el área bajo una
función).
𝐿 = lim
4→<
3|𝑃1c6𝑃1|
4
156
La expresión anterior nos ayudará a encontrar la longitud de las rectas poligonales
inscritas en la curva. Profundizando aún más:
|𝑃1c6𝑃1| = w(𝑥1 − 𝑥1c6)C + (𝑦1 − 𝑦1c6)C
|𝑃1c6𝑃1| = w(∆𝑥)C + (∆𝑦)C
La expresión anterior es para calcular la longitud entre dos puntos. Entonces, sabiendo
que:
𝑚 = 𝑓y(𝑥) =
∆𝑦
∆𝑥
∆𝑦 = 𝑓y
(𝑥) ∙ ∆𝑥
Reemplazando:
|𝑃1c6𝑃1| = w(∆𝑥)C + [𝑓y(𝑥) ∙ ∆𝑥]C
|𝑃1c6𝑃1| = w(∆𝑥)C + [𝑓y(𝑥)]C[∆𝑥]C
|𝑃1c6𝑃1| = w(1 + [𝑓y(𝑥)]C)[∆𝑥]C
|𝑃1c6𝑃1| = w1 + [𝑓y(𝑥)]C ∙ w[∆𝑥]C
|𝑃1c6𝑃1| = w1 + [𝑓y(𝑥)]C ∙ ∆𝑥
Por tanto:
𝐿 = lim
4→<
3|𝑃1c6𝑃1|
4
156
= 𝐿 = lim
4→<
3 w1 + [𝑓y(𝑥)]C ∙ ∆𝑥
4
156

25. Aplicación de la integral – Integral de área e integral de longitud
25
©
Universidad
Estatal
de
Milagro
–
UNEMI
Y ya sabemos que a esta expresión también la podemos expresar como:
𝐿 = E w1 + [𝑓y(𝑥)]C
F
G
𝑑𝑥
En conclusión, tenemos el siguiente teorema:
Longitud de curvas planas: ejemplos.
Ejemplo 8: Encuentre la longitud de arco de la curva 𝑓(𝑥) = 𝑥
S
C
z
, en el intervalo [1, 4]
Teorema 4: Si 𝑓y
es continua sobre el intervalo [𝑎, 𝑏], entonces se dice que la longitud
de una curva expresada como 𝑦 = 𝑓(𝑥), donde 𝑎 ≤ 𝑥 ≤ 𝑏 es:
𝐿 = E w1 + [𝑓y(𝑥)]C
F
G
𝑑𝑥
Figura 13. Gráfica ejemplo 8
Fuente: Elaboración propia

26. Aplicación de la integral – Integral de área e integral de longitud
26
©
Universidad
Estatal
de
Milagro
–
UNEMI
En primer lugar, debemos calcular la derivada de la función:
𝑓y(𝑥) =
3
2
𝑥
6
C
z
Ahora, utilizamos la integral propuesta en el teorema:
𝐿 = E w1 + [𝑓y(𝑥)]C
F
G
𝑑𝑥 = E |1 + d
3
2
𝑥
6
C
z
e
C
k
6
𝑑𝑥
𝐿 = E |1 +
9
4
𝑥
k
6
𝑑𝑥
Simplificando
𝐿 = E V
4 + 9𝑥
4
X
6/C
k
6
𝑑𝑥 = E
1
2
(4 + 9𝑥)6/C
𝑑𝑥
k
6
Integramos aplicando el método de integración de una función compuesta:
𝐿 =
1
(2)(9)
E 9 (4 + 9𝑥)6/C
𝑑𝑥
k
6
=
1
18
d
2
3
(4 + 9𝑥)
S
C
z
e
6
k
= d
1
27
(4 + 9𝑥)
S
C
z
e
6
k
𝐿 = d
1
27
(4 + 9(4))
S
C
z
e − d
1
27
(4 + 9(1))
S
C
z
e
𝐿 = d
1
27
(4 + 36)
S
C
z
e − d
1
27
(4 + 9)
S
C
z
e = d
1
27
(40)
S
C
z
e − d
1
27
(13)
S
C
z
e
𝐿 =
1
27
~(40)
S
C
z
− (13)
S
C
z
• 𝑢
Puede darse la situación donde la curva tenga la siguiente ecuación 𝑥 = 𝑓(𝑦); entonces,
la expresión matemática para calcular su área es:
𝐿 = E w1 + [𝑓y(𝑦)]C
F
G
𝑑𝑦

27. Aplicación de la integral – Integral de área e integral de longitud
27
©
Universidad
Estatal
de
Milagro
–
UNEMI
Ejemplo 9: Encuentre la longitud de arco de la curva 𝑓(𝑦) = 𝑦C
, en el intervalo [0, 1]
Graficamos la curva:
Derivamos 𝑓(𝑦):
𝑓y(𝑦) = 2𝑦
Aplicamos la fórmula:
𝐿 = E w1 + [𝑓y(𝑦)]C
F
G
𝑑𝑦 = E w1 + [2𝑦]C
6
O
𝑑𝑦 = E w1 + 4𝑦C
6
O
𝑑𝑦
Integramos, utilizando el método de integración de sustitución trigonométrica:
𝐿 = E w1 + 4𝑦C
6
O
𝑑𝑦
Donde:
𝑦 =
1
2
tan 𝜃
𝑑𝑦 =
1
2
secC
𝜃𝑑𝜃
Figura 14. Gráfica ejemplo 9
Fuente: Elaboración propia

28. Aplicación de la integral – Integral de área e integral de longitud
28
©
Universidad
Estatal
de
Milagro
–
UNEMI
Entonces:
𝐿 = E w1 + 4𝑦C
6
O
𝑑𝑦 = E |1 + 4 V
1
2
tan 𝜃X
C
6
O
∙
1
2
secC
𝜃𝑑𝜃
= E |1 + 4 V
1
4
tanC𝜃X
6
O
∙
1
2
secC
𝜃𝑑𝜃
𝐿 =
1
2
E w1 + tanC𝜃
6
O
∙ secC
𝜃𝑑𝜃 =
1
2
E sec 𝜃
6
O
∙ secC
𝜃𝑑𝜃 =
1
2
E secS
𝜃
6
O
𝑑𝜃
𝐿 =
1
2
∙
1
2
[sec 𝜃 ∙ tan 𝜃 + ln|sec 𝜃 + tan 𝜃|]O
6
Realizando el cambio de variable y sustituyendo los límites:
𝐿 =
√5
2
+
ln(√5 + 2)
4
𝑢

29. Aplicación de la integral – Integral de área e integral de longitud
29
©
Universidad
Estatal
de
Milagro
–
UNEMI
3. Recursos complementarios
Los siguientes recursos complementarios son sugerencias para que se pueda ampliar la
información sobre el tema trabajado, como parte de su proceso de aprendizaje
autónomo:
» INTEGRALES - Clase Completa: Explicación Desde Cero | El Traductor. (2019).
Recuperado el 4 November 2019, de
o https://www.youtube.com/watch?v=Ec-cGjh0Fr0&t=516s
» Calcular el área entre dos curvas | Khan Academy en Español. (2017).
Recuperado el 14 Diciembre 2019, de
o https://www.youtube.com/watch?v=pW0kTRA6DdI
» Ejemplo de longitud de arco por integración. (2014). Recuperado el 14 Diciembre
2019, de
o https://www.youtube.com/watch?v=iR5I2xv1OUE

30. Aplicación de la integral – Integral de área e integral de longitud
30
©
Universidad
Estatal
de
Milagro
–
UNEMI
4. Bibliografı́a
» Allen, A. (2008). Álgebra intermedia. México: PEARSON EDUCACIÓN. Obtenido
de
https://www.cimat.mx/ciencia_para_jovenes/bachillerato/libros/algebra_angel
_cap7.pdf
» Ayres, F. (1974). Cálculo diferencial e integral. México D.F.: LITOGRÁFICA
INGRAMEX S.A.
» Granville, W. (2009). Cálculo diferencial e integral. Limusa, México: EDITORIAL
LIMUSA S.A.
» Larson, R., & Edwards, B. (2010). Cálculo 1 de una variable. México D.F:
McGRAW-HILL/INTERAMERICANA EDITORES S.A.
» Pérez González, J. (s.f.). Cálculo diferencial e integral de funciones de una
variable. Granada: Departamento de análisis matemático: Universidad de
Granada.
» Purcell, E., Varberg, D., & Rigdon, S. (2007). Cálculo diferencial e integral. México:
PEARSON EDUCACIÓN.
» Rey Pastor, J., Pi Calleja, P., & Trejo, C. (1969). Análisis matemático. Buenos Aires:
EDITORIAL KAPELUSZ S.A.
» Stewart, J. (2012). Cálculo de una variable. México D.F.: Cengage Learning
Editores S.A.
» Thomas, G. (2006). Cálculo. Una variable. México: PEARSON EDUCACIÓN.
» Villena M. (2008). Cálculo Integral.