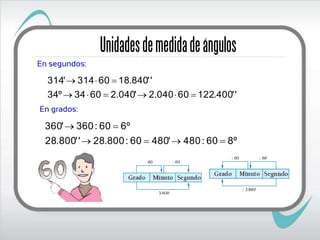
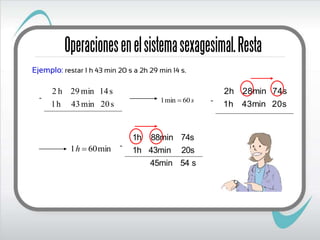
El documento describe el sistema sexagesimal, que se utiliza para medir ángulos y tiempos. En este sistema, 60 unidades de un orden forman 1 unidad del orden superior. Por ejemplo, 60 segundos forman 1 minuto y 60 minutos forman 1 hora. El sistema se utiliza para expresar medidas de ángulos y tiempo de forma compleja o incompleja.

1. Sistemasexagesimal
El sistema sexagesimal es un conjunto de unidades y
reglas, que se utiliza para medir ángulos y tiempos. En la
vida cotidiana lo aplicamos continuamente.

2. Esquemadecontenidos
Sistema sexagesimal
Definición
Unidades de medida de ángulos
Unidades de tiempo
Formas complejae incompleja
Expresiones compleja e incompleja
Paso de forma compleja a incompleja
Paso de forma incompleja a compleja
Operaciones en el SS
Suma
Resta
Multiplicación
División

3. El sistema sexagesimal es el conjunto de unidades y
reglas que se utiliza para medir ángulos y tiempos.
Se denomina sexagesimal porque 60 unidades de un
orden forman 1 unidad del orden superior.
Sistemasexagesimal
ángulos tiempo

4. La unidad de medida de ángulos en el sistema sexagesimal es el grado.
Unidadesdemedidadeángulos
Un grado es el ángulo que resulta de dividir un ángulo recto en 90 partes
iguales.
Para medir ángulos con más precisión y
exactitud, se utilizan unidades menores que el
grado: el minuto y el segundo.
Unidad Símbolo Equivalencia
Grado  1º = 60’
Minuto ‘ 1’ = 60’’
Segundo “ 1” = 3.600’’

5. Unidadesdemedidadeángulos
'
'
400
.
122
60
040
.
2
'
040
.
2
60
34
º
34
'
'
840
.
18
60
314
'
314









En segundos:
En grados:
º
8
60
:
480
'
480
60
:
800
.
28
'
'
800
.
28
º
6
60
:
360
'
360







6. Las unidades de medida de tiempo son el siglo, el año, el mes, el día…
Unidadesdetiempo
Unidad Símbolo Equivalencia
Hora h 1h = 60 min
Minuto min 1min = 60 s
Segundo s 1h = 3.600 s
Para medir periodos de tiempo menores que el día utilizamos
la hora, el minuto y el segundo.
Forman un sistema sexagesimal, cada unidad es 60 veces
mayor que la unidad inferior y 60 veces menor que la
unidad superior.

7. En segundos:
En horas
s
h
s
800
.
10
60
180
min
180
60
3
3
440
.
1
60
24
min
24









h
h
s
7
60
:
420
min
420
5
60
:
300
min
300
60
:
000
.
18
000
.
18






Unidadesdetiempo

8. Expresionescomplejaseincomplejas
Una medida de ángulos o de tiempo puede ser expresada de dos
maneras:
Forma compleja, o utilizando varias unidades
Forma incompleja, o utilizando una sola unidad
s
h 14
min
35
2 '
39'
15'
º
26
h
3,7
º
28
min
4
'
'
178

9. Pasodeformacomplejaaincompleja
Para transformar una medida de ángulos o tiempo de forma compleja
a incompleja, hay que considerar las equivalencias entre unidades:
Horas o grados a minutos, se multiplica por 60
Horas o grados a segundos, se multiplica por 3.600
Minutos a segundos, se multiplica por 60
Ejemplo: '
'
37
'
25
º
14
'
51.937'
'
'
37
'
25
º
14
'
37'
'
'
500
.
1
60
25
'
25
'
'
400
.
50
600
.
3
14
º
14








10. Pasodeformacomplejaaincompleja
Ejemplo:
s
8.005
s
25
min
13
h
2
s
25
780
60
13
min
3
1
200
.
7
600
.
3
2
2







s
s
h
Ejemplo: s
25
min
13
h
2
min
28
h
3
s
12.480
min
3h28
680
.
1
60
28
min
28
800
.
10
600
.
3
3
3







s
s
h

11. Pasodeformaincomplejaacompleja
Para transformar una medida de ángulos o tiempo de forma incompleja
a compleja, hay que considerar que:
• Si dividimos segundos entre 60, obtenemos
como cociente minutos y como resto segundos.
• Si dividimos minutos entre 60, obtenemos
como cociente grados y como resto minutos.

12. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
Ejemplo: expresar 5.578 s en forma compleja.

13. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
Ejemplo: expresar 5.578 s en forma compleja.
25
325
452
60
525
.
34

14. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
Ejemplo: expresar 5.578 s en forma compleja.
25
325
5
452
60
525
.
34

15. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
Ejemplo: expresar 5.578 s en forma compleja.
25
325
57
452
60
525
.
34

16. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
Ejemplo: expresar 5.578 s en forma compleja.

17. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
Ejemplo: expresar 5.578 s en forma compleja.
60
75
5

18. Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
Ejemplo: expresar 5.578 s en forma compleja.

19. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
'
'
25
'
35
º
9
'
'
525
.
34 

20. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
'
'
25
'
35
º
9
'
'
525
.
34 
60
578
.
5

21. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
'
'
25
'
35
º
9
'
'
525
.
34 
9
178
60
578
.
5

22. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
58
92
178
60
578
.
5
'
'
25
'
35
º
9
'
'
525
.
34 

23. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
58
92
178
60
578
.
5
60
2
9
'
'
25
'
35
º
9
'
'
525
.
34 

24. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25
325
575
452
60
525
.
34
9
35
60
75
5
58
92
178
60
578
.
5
1
32
60
2
9
'
'
25
'
35
º
9
'
'
525
.
34 

25. Ejemplo: expresar 5.578 s en forma compleja.
Pasodeformaincomplejaacompleja
Ejemplo: expresar 34.525’’ en grados, minutos y segundos.
25"
325
575'
452
60
"
525
.
34
9º
35'
60
'
75
5
s
58
min
92
178
60
s
578
.
5
h
1
min
32
60
min
2
9
s
h
s 58
min
32
1
578
.
5 
'
'
25
'
35
º
9
'
'
525
.
34 

26. Para sumar medidas de ángulos o de tiempo se colocan
los sumandos agrupados: grados con grados, minutos
con minutos y segundos con segundos.
Una vez obtenido el resultado, hay que
tener en cuenta:
• Si los segundos sobrepasan 60,
los transformamos en minutos.
• Si los minutos sobrepasan 60,
los transformamos en horas.
Operacionesenelsistemasexagesimal.Suma

27. Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
Operacionesenelsistemasexagesimal. Suma

28. Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
+
'
48'
37'
14º
'
37'
24'
7º
Operacionesenelsistemasexagesimal.Suma

29. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
+

30. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
+
'
'
25
'
1
'
25
'
'
60
'
'
85 




31. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
'
25'
62'
21º
'
1
+
+
'
'
25
'
1
'
25
'
'
60
'
'
85 




32. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
'
25'
62'
21º
'
1
'
2
º
1
'
2
'
60
'
62 



+
+
'
'
25
'
1
'
25
'
'
60
'
'
85 




33. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
'
25'
62'
21º
'
1
'
2
º
1
'
2
'
60
'
62 



º
1
'
25'
2'
22º
+
+
+
'
'
25
'
1
'
25
'
'
60
'
'
85 




34. Operacionesenelsistemasexagesimal.Suma
Ejemplo: sumar los ángulos 7º 25’ 37’’ y 14º 37’ 48’’.
'
85'
61'
21º
'
48'
37'
14º
'
37'
24'
7º
'
25'
62'
21º
'
1
'
2
º
1
'
2
'
60
'
62 



º
1
'
25'
2'
22º
'
'
25
'
2
º
22
'
'
54
'
37
º
14
'
'
37
'
25
º
7 

+
+
+
'
'
25
'
1
'
25
'
'
60
'
'
85 




35. Operacionesenelsistemasexagesimal.Resta
Para restar medidas de ángulos o de tiempo se colocan
el minuendo y el sustraendo agrupados: grados con
grados (u horas con horas), minutos con minutos y
segundos con segundos.
Una vez obtenido el resultado, hay que
tener en cuenta:
• Si el número de segundos del minuendo
es menor que el del sustraendo, se pasa un
minuto del minuendo a segundos.
• Si el número de minutos del minuendo es
menor que el del sustraendo, se pasa una
hora del minuendo a minutos.

36. Operacionesenelsistemasexagesimal.Resta
- s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

37. Operacionesenelsistemasexagesimal.Resta
- s
60
min
1 
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

38. Operacionesenelsistemasexagesimal.Resta
-
20s
43min
1h
74s
28min
2h
-
s
60
min
1 
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

39. Operacionesenelsistemasexagesimal.Resta
-
20s
43min
1h
74s
28min
2h
-
s
60
min
1 
min
60
1 
h
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

40. Operacionesenelsistemasexagesimal.Resta
-
20s
43min
1h
74s
28min
2h
-
-
s
60
min
1 
min
60
1 
h
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.
20s
43min
1h
74s
88min
1h

41. Operacionesenelsistemasexagesimal.Resta
-
20s
43min
1h
74s
28min
2h
-
s
54
45min
20s
43min
1h
74s
88min
1h
-
s
60
min
1 
min
60
1 
h
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

42. Operacionesenelsistemasexagesimal.Resta
-
20s
43min
1h
74s
28min
2h
-
s
54
45min
20s
43min
1h
74s
88min
1h
-
s
54
min
45
s
60
min
1 
min
60
1 
h
s
20
min
43
h
1
s
14
min
29
h
2
Ejemplo: restar 1 h 43 min 20 s a 2h 29 min 14 s.

43. Para multiplicar medidas de ángulos o de tiempo por un número natural:
1. Multiplicamos cada unidad por el número natural.
2. Efectuamos las conversiones y agrupamientos necesarios.
Ejemplo: efectuar 5
)
'
'
18
'
14
º
32
( 
'
90'
70'
160º
5
'
18'
14'
32º

'
1
'
30'
130'
º
160
º
2
'
30'
10'
º
162
'
'
30
'
1
'
'
30
'
'
60
'
'
90 



'
10
º
2
'
10
'
60
'
60
'
130 




Operacionesenelsistemasexagesimal.Multiplicación

44. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar 3
)
36
min
24
3
( 
s
h
3
36s
24min
3h


45. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar
108s
72min
3h
3
36s
24min
3h

3
)
36
min
24
3
( 
s
h

46. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar
s
108
min
72
h
3
3
s
36
min
24
h
3

s
s
s
s 48
min
1
48
60
108 



3
)
36
min
24
3
( 
s
h

47. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar
108s
72min
3h
3
36s
24min
3h

min
1
48s
73min
h
3
s
s
s
s 48
min
1
48
60
108 



3
)
36
min
24
3
( 
s
h

48. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar
108s
72min
3h
3
36s
24min
3h

min
1
s
48
min
73
h
3
s
s
s
s 48
min
1
48
60
108 



min
13
1
min
13
'
60
min
73 


 h
3
)
36
min
24
3
( 
s
h

49. Operacionesenelsistemasexagesimal.Multiplicación
Ejemplo: efectuar
108s
72min
3h
3
36s
24min
3h

min
1
48s
73min
h
3
h
1
48s
13min
h
4
s
s
s
s 48
min
1
48
60
108 



min
13
1
min
13
'
60
min
73 


 h
3
)
36
min
24
3
( 
s
h

50. Para dividir medidas de ángulos o de tiempo por un
número natural:
1. Dividimos los grados (u horas) entre el número
natural.
2. Transformamos el resto de grados (u horas) en
minutos y se añaden a los que ya tenemos. Luego
dividimos los minutos que resultan entre el número
natural.
3. Pasamos el resto de minutos a segundos y se
añaden a los que ya teníamos. Luego los dividimos
entre el número natural.
Operacionesenelsistemasexagesimal.División

51. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar . 2
:
)
'
'
15
'
51
º
71
(
1
11
2
'
15'
51'
º
71

52. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar . 2
:
)
'
'
15
'
51
º
71
(
1
11
2
'
15'
51'
º
71

53. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar . 2
:
)
'
'
15
'
51
º
71
(
1
35º
11
2
'
15'
51'
º
71

54. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar .
60'
º
1 
2
:
)
'
'
15
'
51
º
71
(
1
11
111'
60'
1
55'
35º
11
2
'
15'
51'
º
71

55. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar .
60'
º
1 
'
60'
'
1
2
:
)
'
'
15
'
51
º
71
(
'
60'
1
11
111'
60'
1
55'
35º
11
2
'
15'
51'
º
71

56. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar .
'
1'
15
'
75'
'
60'
1
11
111'
60'
1
'
37'
55'
35º
11
2
'
15'
51'
º
71
60'
º
1 
'
60'
'
1
2
:
)
'
'
15
'
51
º
71
(

57. Operacionesenelsistemasexagesimal.División
Ejemplo: efectuar .
'
1'
15
'
75'
'
60'
1
11
111'
60'
1
'
37'
55'
35º
11
2
'
15'
51'
º
71
60'
º
1 
'
60'
'
1
resto
cociente
2
:
)
'
'
15
'
51
º
71
(