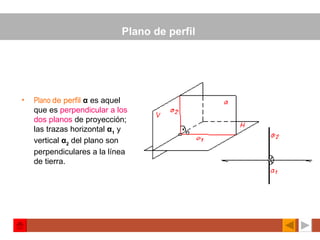
El documento describe los elementos básicos del sistema diédrico de representación, incluyendo la proyección de puntos, rectas y planos, así como sus posiciones relativas. Explica cómo representar estos elementos geométricos mediante proyecciones cilíndricas ortogonales y sus trazas sobre los planos de proyección horizontal y vertical.

1. S.DIÉDRICO PART 1 Tema 8 Sistemas de representación Sistema diédrico El punto La recta El plano Posiciones del plano Tercera proyección ENLACES Diseño y desarrollo: Rafael quintero fundamentos 35horas de 39 PRUEBA 4ª 8 UNIDAD 10. SISTEMA AXONOMÉTRICO Y CABALLERA 13 UNIDAD 9. SISTEMA DIÉDRICO: FIGURAS PRUEBA 3ª 6 UNIDAD 8. SISTEMA DIÉDRICO: MÉTODOS 6 UNIDAD 7. SISTEMA DIÉDRICO: POSICIONES RELATIVAS 6 UNIDAD 6. SISTEMA DIÉDRICO: PUNTO, RECTA Y PLANO

2. LETRAS GRIEGAS QUE SE USARÁN varphi pi delta beta gamma alpha

3. Sistema diédrico: punto, recta y plano:

6. SISTEMA DIEDRICO ELEMENTOS DEL SISTEMA DIEDRICO

8. Representación del punto Dibujo Técnico 2.º BACHILLERATO 9 Elementos del sistema diédrico: PH: Plano horizontal de proyección PV: Plano vertical de proyección LT: Línea de tierra A 1 : Proyección horizontal del punto A 2 : Proyección vertical del punto c: cota del punto a: alejamiento del punto

9. Definiciones sobre el punto

10. POSICIONES DEL PUNTO

19. La recta REPRESENTACiÓN DE LA RECTA

20. Representación de la recta Dibujo Técnico 2.º BACHILLERATO 9 2 r 1 : Proyección horizontal de la recta r 2 : Proyección vertical de la recta H r : Traza horizontal de la recta V r : Traza vertical dela recta

25. Aprende a dibujar una recta, en el espacio y en diédrico ayuda

26. Ahora lo vamos hacer al contrario

28. Representación de la recta (II) Dibujo Técnico 2.º BACHILLERATO 9 3 r 1 : Proyección horizontal de la recta r 2 : Proyección vertical de la recta H r : Traza horizontal de la recta V r : Traza vertical dela recta

30. POSICIONES DE la recta

37. El plano Representación del plano

39. Representación del plano Dibujo Técnico 2.º BACHILLERATO 9  1 : Traza horizontal del plano  2 : Traza vertical del plano

41. RECTAS CONTENIDAS EN UN PLANO

42. Rectas contenidas en un plano (I) Dibujo Técnico 2.º BACHILLERATO 9 Condiciones para que una recta esté contenida en un plano: 1º La traza horizontal de r debe estar en la traza horizontal de  2º La traza vertical de r debe estar en la traza vertical de 

43. Rectas contenidas en un plano (II) Dibujo Técnico 2.º BACHILLERATO 9 Recta horizontal del plano La proyección horizontal de la recta es paralela a la traza horizontal del plano La proyección vertical de la recta es paralela a la línea de tierra Recta frontal del plano La proyección horizontal de la recta es paralela a la línea de tierra La proyección vertical de la recta es paralela a la traza vertical del plano

46. Rectas contenidas en un plano (III) Dibujo Técnico 2.º BACHILLERATO 9 Recta de máxima pendiente del plano La proyección horizontal de la recta es perpendicular a la traza horizontal del plano Recta de máxima inclinación del plano La proyección vertical de la recta es perpendicular a la traza vertical del plano

51. Posiciones del plano

59. PLANO DEFINIDO POR DOS RECTAS QUE SE CORTAN

61. Dadas las rectas r y s que se cortan en el punto P α 1 α 2 1 Se hallan las trazas H r y V r de la recta r . 2 Se hallan las trazas H s y V s de la recta s . 3 La recta que une las dos trazas horizontales H r y H s de las rectas es la traza horizontal α 1 del plano a solicitado. 4 La recta que une las dos trazas verticales V r y V s de las rectas es la traza vertical α 2 del plano α . Como comprobación, las dos trazas α 1 y α 2 se cortan en el mismo punto de la línea de tierra.

68. Observa cómo localizar la tercera proyección A´´ , que resulta de pasar un plano de perfil (por ejemplo por el origen).

72. fin Creado por rafael quintero durante el curso 2003/04