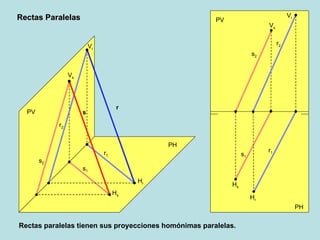
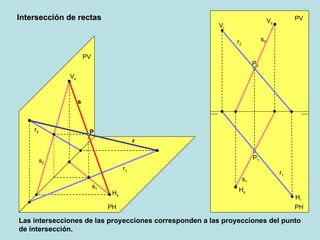
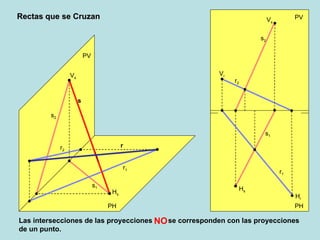
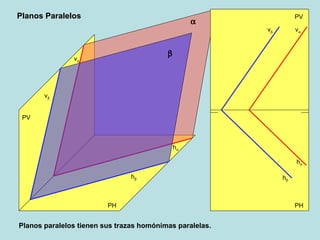
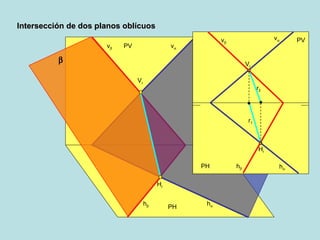
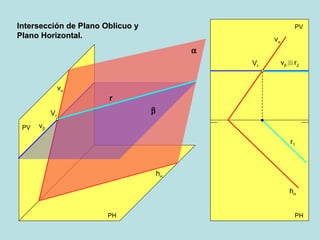
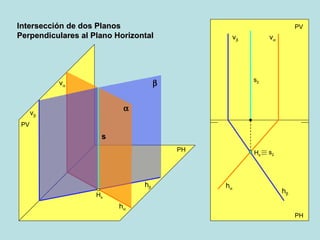
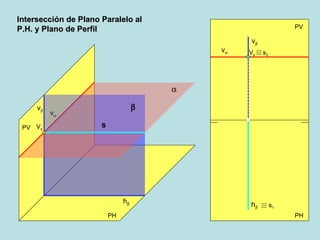
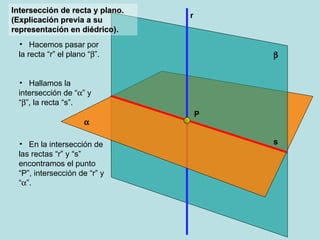
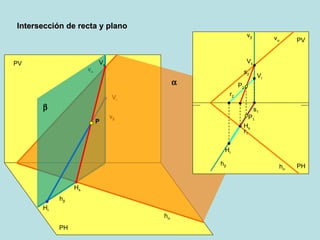
El documento describe las posiciones relativas entre rectas y planos en un sistema diédrico. Explica que las rectas y planos paralelos tienen sus proyecciones homónimas paralelas, y que la intersección de las proyecciones corresponde a la proyección del punto de intersección. También describe cómo representar gráficamente en el sistema diédrico la intersección entre una recta y un plano, y entre diferentes configuraciones de planos.

1. SISTEMA DIÉDRICO Posiciones relativas entre rectas y planos. Intersección y Paralelismo

2. Rectas Paralelas PV PH PH PV H s s 2 V r s s 1 s 1 s 2 V s H s r 2 V r r 1 H r r r 2 r 1 Rectas paralelas tienen sus proyecciones homónimas paralelas. H r V s

3. Intersección de rectas PV PH PH PV H s s 2 V s s s 1 s 1 s 2 V s H s r 2 V r r 1 H r P P 2 P 1 r r 2 r 1 Las intersecciones de las proyecciones corresponden a las proyecciones del punto de intersección.

4. Rectas que se Cruzan PV PH PH PV H s s 2 V s s s 1 s 1 s 2 V s H s r 2 V r r 1 H r r r 2 r 1 Las intersecciones de las proyecciones se corresponden con las proyecciones de un punto. NO

5. Planos Paralelos PV PH h  v  PH PV h  v   h  v  h  v  Planos paralelos tienen sus trazas homónimas paralelas. 

6. Intersección de dos planos oblícuos PH PV h  v  v  h    V r H r PH PV h  v  v  h  r 2 r 1 H r V r

7. Intersección de Plano Oblicuo y Plano Horizontal. PV PH PH PV h  v  h  v  v    V r r r 1 r 2 v  V r

8. Intersección de dos Planos Perpendiculares al Plano Horizontal PV PH PH PV h  v  h  v    h  v  H s s h  v  H s s 2 s 2

9. Intersección de Plano Paralelo al P.H. y Plano de Perfil PV PH PH PV v   v  h  v  h  v   V s s 1 s 2 s V s

10.   r s P Intersección de recta y plano. (Explicación previa a su representación en diédrico). Hallamos la intersección de “  ” y “  ”, la recta “s”. En la intersección de las rectas “r” y “s” encontramos el punto “P”, intersección de “r” y “  ”. Hacemos pasar por la recta “r” el plano “  ”.

11. PH PV h  v  v  h  V r H r Intersección de recta y plano   P  PH PV h  v  H s V s h  v  r 1 r 2 V r H r H s V s s 2 s 1 P 1 P 2