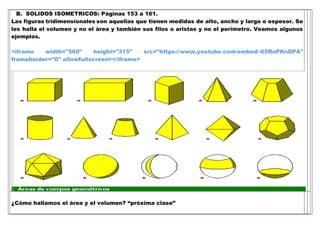
Este documento resume las actividades de clase de matemáticas de varios días para estudiantes de quinto grado. Incluye operaciones con fracciones decimales y porcentajes, máximo común divisor y mínimo común múltiplo, razones y proporciones, regla de tres, áreas y volúmenes de figuras geométricas, y estadísticas como tablas y medidas de tendencia central. Los estudiantes aprendieron conceptos a través de ejemplos y ejercicios de libros de texto, y se les asignó tarea relacion

1. CITY: Santiago de Cali. DATE: Tuesday, August 2 nd. 2016. WEEK: 23
SUBJECT: MATHEMATIC 5º TOPIC: Operaciones con decimales.
Porcentajes.
CLASS: 45.
Activity in Class:
Con este cuadro se realizó el examen.
FRACCION DECIMAL PORCENTAJE AMPLIFICACION FRACCION DECIMAL PORCENTAJE AMPLIFICACION
1/2 3/5
1/3 4/5
1/4 3/2
1/5 5/2
2/3 1/1
2/5 5/5
3/4 10/10
Se operaron las siguientes fracciones:
(9/5) y (7/8)
Se operaron los siguientes decimales:
98.76 y 3.54 “explicación como clases anteriores”
HOMEWORK:

2. CITY: Santiago de Cali. DATE: Thursday, August 4 th. 2016. WEEK: 23
SUBJECT: MATHEMATIC 5º TOPIC: mcm y MCD,
Razones y Proporciones.
CLASS: 46.
Activity in Class:
Con este cuadro se realizó el examen.
FRACCION DECIMAL PORCENTAJE AMPLIFICACION FRACCION DECIMAL PORCENTAJE AMPLIFICACION
1/2 3/5
1/3 4/5
1/4 3/2
1/5 5/2
2/3 1/1
2/5 5/5
3/4 10/10
Se operaron las siguientes fracciones:
(9/8) y (6/7)
Se operaron los siguientes decimales:
98.76 y 5.4

3. MAXIMO COMUN DIVISOR y mínimo común múltiplo Páginas 36 y 37 del libro.
“todo o nada” “Todos hasta uno”
MCD:
Es simplificar los números al máximo, donde los dos tienen o no tienen divisibilidad, los dos o nada.
mcm:
Es simplificar los números al máximo con mitades, tercera, quinta, donde todos los llevo hasta uno.
Hallar el MCD y el mcm de los siguientes números: (12 y 16) y (18 24 y 30) y (36 48 y 60).
MCD “todo o nada”
12 16 I 2
6 8 I 2
3 4 I
I MCD (12 y 16) = 2 x 2 = 4
mcm “todo a uno”
12 16 I 2
6 8 I 2
3 4 I 2
3 2 I 2
3 1 I 3
1 1 I
I mcm (12 y 16) = 2 x 2 x 2 x 2 x 3 = 16 x 3 = 48
Consulta……. ¿Qué es una razón?....... ¿Qué es una proporción?....... ¿Qué es una regla de tres?
“explicación próxima clase”

4. PROXIMOS TEMAS A TRABAJAR:
- MCD, mcm, razones, proporciones y regla de tres
- Potenciación, radicación y logaritmación
- Medidas (magnitudes, múltiplos, submúltiplos, MKS, CGS)
- Plano cartesiano (ángulos, triángulos, transformaciones, proyecciones)
- Figuras y solidos geométricos
- Tablas y graficas estadísticas. Medidas de tendencia central
HOMEWORK: Realizar páginas 36 y 37 del libro.
Consulta……. ¿Qué es una razón?....... ¿Qué es una proporción?....... ¿Qué es una regla de tres?

5. CITY: Santiago de Cali. DATE: Tuesday, August 9 th 2016. WEEK: 24
SUBJECT: MATHEMATIC 5º TOPIC: Razones y proporciones,
Regla de tres.
Operaciones con decimales.
CLASS: 47.
Activity in Class:
Razón:
Cociente que se usa para comparar dos cantidades o magnitudes. Su representación puede ser:
1
---- ½ 1 2 1 2 1 : 2 “se lee: 1 es a 2”
2
Proporciones : Cuando dos razones son equivalentes.
1 5
---- = ------ 1:2 :: 5:10 “se lee: uno es a dos como cinco es a diez”
2 10
HOMEWORK: Realizar páginas 180 a 183 del libro.

6. CITY: Santiago de Cali. DATE: Tuesday, August 11 th 2016. WEEK: 24
SUBJECT: MATHEMATIC 5º TOPIC: Regla de tres.
Operaciones con decimales.
CLASS: 48.
Activity in Class:
Una regla de tres, es una herramienta matemática que nos ayuda a hallar el segundo valor de una
razón, que es el cuarto valor en una proporción.
Ejemplo:
1 x
---- = ------ 1:2 :: x:10 “se lee: uno es a dos como x es a diez”
2 10
Me debo preguntar…….¿Que le hago a dos para que se convierta en 10?.......”lo multiplico por 5”
Entonces……a el numero 1 también lo multiplico por 5………y me queda……
1 5
---- = ------ 1:2 :: 5:10 “se lee: uno es a dos como 5 es a diez”
2 10
Resuelve la siguiente proporción, aplicando una regla de tres…….
Para el desayuno de 5 personas, se recogieron $10000 pesos…….si llegan 3 personas más…….
¿Cuánto debo recoger?

8. PROXIMOS TEMAS A TRABAJAR:
- Regla de tres, Potenciación, radicación y logaritmación
- Plano cartesiano (ángulos, triángulos, transformaciones, proyecciones)
- Figuras y solidos geométricos
- Tablas y graficas estadísticas. Medidas de tendencia central
HOMEWORK: Realizar páginas 186 a 189 del libro.

9. CITY: Santiago de Cali. DATE: Tuesday, August 16 th 2016. WEEK: 25
SUBJECT: MATHEMATIC 5º TOPIC: Regla de tres (aclaraciones)
Potenciación, Radicación y
Logaritmación. Pág. 27 a 35.
CLASS: 49.
Activity in Class:

10. PROXIMOS TEMAS A TRABAJAR:
- Plano cartesiano (ángulos, triángulos, transformaciones, proyecciones)
- Figuras y solidos geométricos
- Tablas y graficas estadísticas. Medidas de tendencia central
HOMEWORK: Resolver en el libro páginas 27 a 35.

11. CITY: Santiago de Cali. DATE: Thursday, August 18 th 2016. WEEK: 25
SUBJECT: MATHEMATIC 5º TOPIC: Potenciación, Radicación y
Logaritmación. Pág. 27 a 35.
CLASS: 50
Activity in Class:
Numero al
cuadrado
Multiplicación Potencia
Cuadrada
Numero al
cubo
Multiplicación Potencia
Cubica
Radicando
2
√ x
Raíz
Cuadrada
Radicando
3
√ x
Raíz
Cubica
1 2
1 x 1 1 1 3
1 2
√ 1 1 3
√ 1 1
2 2
4 2 3
8 2
√ 4 2 3
√ 8 2
3 2
9 3 3
3 x 3 x 3 27 2
√ 9 3 3
√ 27 3
4 2
16 4 3
64 2
√ 16 4 3
√ 64 4
5 2
5 x 5 25 5 3
125 2
√ 25 5 3
√ 125 5
6 2
36 6 3
216 2
√ 36 6 3
√ 216 6
7 2
49 7 3
7 x 7 x 7 343 2
√ 49 7 3
√ 343 7
8 2
64 8 3
512 2
√ 64 8 3
√ 512 8
9 2
81 9 3
729 2
√ 81 9 3
√ 729 9
10 2
10 x 10 100 10 3
1000 2
√ 100 10 3
√ 1000 10
11 2
121 11 3
1331 2
√ 121 11 3
√ 1331 11
12 2
144 12 3
12 x 12 x 12 1728 2
√ 144 12 3
√ 1728 12
13 2
169 13 3
2197 2
√ 169 13 3
√ 2197 13
14 2
196 14 3
2744 2
√ 196 14 3
√ 2744 14
15 2
15 x 15 225 15 3
3375 2
√ 225 15 3
√ 3375 15
Figuras y solidos geometricos

12. 1. Activity in Class:
A. FIGURAS PLANAS. Página 97 a 101……….107 y 111.
Las figuras bidimensionales son aquellas que tienen medidas de alto y ancho. Se les halla el área
y el perímetro (suma de los lados del entorno en la figura). Veamos algunos ejemplos:
<iframe width="560" height="315" src="https://www.youtube.com/embed/BemjvOKSbyk"
frameborder="0" allowfullscreen></iframe>
¿Cómo hallamos el área en cada figura?

13. B. SOLIDOS ISOMETRICOS: Páginas 153 a 161.
Las figuras tridimensionales son aquellas que tienen medidas de alto, ancho y largo o espesor. Se
les halla el volumen y no el área y también sus filos o aristas y no el perímetro. Veamos algunos
ejemplos.
<iframe width="560" height="315" src="https://www.youtube.com/embed/-65RnPKnDPA"
frameborder="0" allowfullscreen></iframe>
¿Cómo hallamos el área y el volumen? “próxima clase”

16. Áreas: Volúmenes:
Cuadrado Lado x Lado Cubo Lado x Lado x Lado
Rectángulo Base x Altura Prisma Base x Altura x Largo
Paralelogramo Base x Altura cilindro
Triangulo (Base x Altura)/ 2 Pirámide
Circulo Esfera
2. Activity in class:
1. Hallar el área del patio de la escuela si tiene 15 metros de ancho y 10 metros de largo.
2. Hallar el área de un parque de forma triangular si tiene de ancho 30 metros y 15 metros de
largo.
3. Hallar es el volumen de un salón si tiene 8 metros de largo, 7 metros de ancho y 2 metros de
alto.
4. Realiza los dibujos de cada ejercicio.
PROXIMOS TEMAS A TRABAJAR:
- Plano cartesiano (ángulos, triángulos, transformaciones, proyecciones)
- Tablas y graficas estadísticas. Medidas de tendencia central
HOMEWORK: Resolver en el libro páginas 111 y 161.

17. CITY: Santiago de Cali. DATE: Tuesday, August 23 rd 2016. WEEK: 26
SUBJECT: MATHEMATIC 5º TOPIC: Áreas y volúmenes. Aplicaciones CLASS: 51 y 52.
Activity in Class: Taller: Resolver las siguientes situaciones.
- Se desea cubrir una piscina con forma circular con una lona, para evitar que se ensucie con
hojas de los árboles en las noches. Si la piscina tiene un radio de 3 metros, ¿Cuál es el área de la
piscina?, ¿Cuánto debo comprar de lona para fabricar el forro? Si la piscina tiene 1.5 metros de
profundidad ¿Cuál es su volumen?

18. - Se desea sembrar pasto en un parque y pintar su perímetro de color verde manzana; este parque
tiene una forma especial y está conformado por la unión de varias figuras geométricas. ¿Cuántos
metros de pasto se necesitan?, ¿Cuál es el perímetro del parque? La forma del parque es:

20. - Se desea rellenar un balón de futbol con arena, para fabricar un instrumento de peso que permita
realizar ejercicios de levantamiento vertical en niños. Si el balón de futbol tiene un radio de 15
cm, ¿Cuánta arena necesito para llenarlo?
Para resolver este ejercicio, debemos hallar el volumen de una esfera así:
El volumen de una esfera es: V(esfera) = (4𝜋𝑟3
) ÷ 3 y su radio es 15 cm.
V (esfera) = (4𝜋𝑟3
) ÷ 3
V (esfera) = (4𝑥(3.14)𝑥(15𝑐𝑚)3
) ÷ 3
V (esfera) = (42390 cm3
) ÷ 3
V(esfera) = 14130 cm3
es la cantidad de arena que necesitamos para llenar el balón.
PROXIMOS TEMAS….
- Tablas y graficas estadísticas. Medidas de tendencia central
HOMEWORK:
Inventar un ejercicio donde necesites hallar el área de un cuadrilátero y el área de un círculo.

21. CITY: Santiago de Cali. DATE: Tuesday, August 30 th 2016. WEEK: 27
SUBJECT: MATHEMATIC 5º TOPIC: Tablas y graficas estadísticas.
Medidas de tendencia central.
CLASS: 53
Activity in Class:
Se realiza una encuesta en el grado 5-1 de la Olga Lucia Lloreda a 35 estudiantes sobre ¿Cuál es su
cantante favorito? Entre 6 opciones, obteniendo los siguientes resultados:
M: Maluma Q: Enrique Iglesias C: Cali y Dandee B: Bruno Mars A: Anuel Z: Zarcort
M, M, Q, C, M, A, B, Z, M, B, M, M, B, M, M, Z, Z, Z, Z, A, M, Z, Z, M, Z, M, Z, Z, M, Z, B, B, M, M, A,
Teniendo en cuenta estos resultados, podemos generar el siguiente tabulado.
Cantante Frecuencia Relativa %
Maluma 14 14/35 = 0,40
E. Iglesias 1 1/35 = 0,02
Cali y Dandee 1 1/35 = 0,02
Bruno Mars 5 5/35 = 0,14
Anuel 3 3/35 = 0,09
Zarcort 11 11/35 = 0,31
35 0,98

22. Ahora veamos las siguientes gráficas:
Medidas de Tendencia Central
Moda: Dato que más se repite. En este ejercicio Maluma está de moda al obtener 14 votos de 35.
Media: Llamado también promedio. En este ejercicio el promedio es:
- Sumamos los datos y lo dividimos por el número de cantantes, es decir, 35/6 = 5.8 = 6
HOMEWORK: Realizar páginas 57 a 60, 165 a 167 y 207 a 210.
14
1 1
5
3
11
M Q C B A Z
Cantantes
Serie 1 Serie 2 Serie 3
0
2
4
6
8
10
12
14
16
M Q C B A Z
Cantantes
Serie 1 Serie 2 Serie 3
40%
3%3%14%
9%
31%
Cantantes
M
Q
C
B
A
Z
0 5 10 15
M
Q
C
B
A
Z
Cantantes
Serie 1 Serie 2 Serie 3