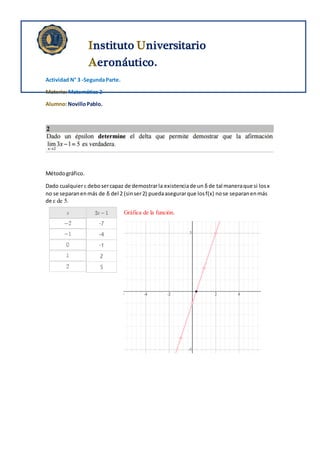
El documento presenta un análisis matemático de una función f(x) = (5-1/x)^2. Se demuestra que para cualquier ε existe un δ tal que si |x-2|<δ, entonces |f(x)-5|<ε. Se grafica la función y se calculan sus límites cuando x tiende a valores específicos, encontrando que el límite existe para todos los casos excepto cuando x tiende a 1/5, donde la función no es continua.

1. Instituto Universitario
Aeronáutico.
Actividad N° 3 -SegundaParte.
Materia: Matemática 2-
Alumno:NovilloPablo.
Métodográfico.
Dado cualquierε debosercapaz de demostrarla existenciade un δde tal maneraque si losx
no se separanenmás de δ del 2 (sinser2) puedaasegurarque losf(x) nose separanenmás
de ε de 5.
Gráfica de la función.

2. Gráfica de rectas horizontales.
SeaP el puntodonde la rectay = 5 – ε corta la gráfica de f, por P trazamos una recta vertical
que corta al eje X en a.
Sea Q el punto donde la recta y= 5 + ε corta la gráfica de f, por Q trazamos una recta vertical
que corta al eje X en b.
Ahora bien, llamamos a las distancias:
2 – a = δ1 (1)
B – 2 = δ2 (2)
Despejando(1).
a = 2 - δ1
y la Segunda(2).
b = 2 + δ2
por locual podemosdecirque:
si x ϵ (a,b)-{2} = (2 - δ1, 2 + δ2 ) – {2} podemosasegurarque f(x) ϵ(5 – ε, 5 + ε)

3. a) Primerose calculael limite partiendode izquierdaaderecha.
Valoresde x cercanosa 1/5 pero menores.
83,0
6
5
)
6
1
( 
9,0
10
9
)
50
9
( 
A medidaque nosacercamosa 1/5 losvaloresde f(x) se acercana 1.
Entoncesdecimosque el límite de f(x) cuandox tiendea1/5 es1.
Ahoracalculamosde derechaa izquierda.
5,1
2
3
)
10
3
( 
25,1
4
5
)
4
1
( 
A medidaque nosacercamosa 1/5 losvaloresde f(x) se acercana 1.
Entoncesdecimosque el límite de f(x) cuandox tiendea1/5 es1.
Tanto de izquierdaaderechacomode derechaa izquierdael límitetiende a1.
Ahorael limite cuandotiende a–(1/5).
lim
𝑥→(−
1
5
)
= 1
5
1
)
5
1
(
)
5
1
()
5
1
(5 2



b)
 La funciónnoescontinuaenel puntox = 1/5 porque no estadefinidapara
dichopunto.
 Es continuaen(-1/5).
c)
Cuandoel limite tiende a+∞.
lim
𝑥→∞
= 


5
1
5 2
x
xx
El limite cuandotiendea+∞ esigual a +∞, ya que si tomamosvalorescada vezmás
grandesde x el resultadode lafunciónescada vezmayor.

4. Cuandoel limite tiende a-∞.
lim
𝑥→−∞
= 


5
1
5 2
x
xx
El limite cuandotiendea-∞esigual a -∞,ya que si tomamosvalorescadavezmás
grandesperocon signonegativode x el resultadode lafunciónescada vezmayorpero
con signonegativo.
d)
Cuandox tiende a-(1/5).

5. Cuandox tiende a1/5.