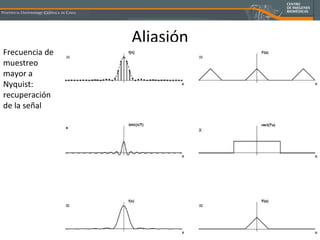
El documento resume conceptos clave de muestreo y reconstrucción de señales en resonancia magnética, incluyendo transformadas de Fourier continuas y discretas, el teorema de Nyquist sobre muestreo, y estrategias para evitar aliasión como muestrear a una frecuencia mayor a la de Nyquist. También presenta ejemplos prácticos usando Matlab para ilustrar estas ideas.

1. Adquisición y reconstrucción de imágenes con resonancia magnética Pablo Irarrázaval Director Centro de Imágenes Biomédicas Pontificia Universidad Católica de Chile Taller

2. Unidades Fundamentos de Resonancia Magnética. Repaso de la teoría del muestreo y análisis de frecuencia. Estrategias de muestreo y reconstrucción en RM

3. ANÁLISIS DE FRECUENCIA Y MUESTREO Unidad 2

4. Temas Transformada de Fourier continua Transformada de Fourier discreta Relación continua – discreta Muestreo y aliasión

5. Transformada de Fourier continua (FT) Se define la transformada de Fourier como Y su inversa como

6. Dimensionalidad en cm (s) adimensional en 1/cm (Hz)

7. Bases de Fourier El conjunto define una base ortonormal

8. Bases de Fourier El conjunto define una base ortonormal

9. Bases de Fourier El conjunto define una base ortonormal

10. Bases de Fourier El conjunto define una base ortonormal

11. Bases de Fourier El conjunto define una base ortonormal

12. Bases de Fourier

13. Ejemplos de pares de Fourier Impulso y uno

14. Ejemplos de pares de Fourier Coseno y horquilla

15. Ejemplos de pares de Fourier Seno y antihorquilla

16. Ejemplos de pares de Fourier Rect y sinc

17. Ejemplos de pares de Fourier Triángulo y sinc cuadrado

18. Ejemplos de pares de Fourier Gauss

19. Ejemplos de pares de Fourier Shah

20. LAB1 Ejemplos de Transformadas Calculemos con Matlab algunos pares de transformadas. Usemos aproximación de Newton

21. EjContFourier.m

22. EjContFourier.m

23. Propiedades de la FT 3. Escalamiento

24. Propiedades de la FT 3. Escalamiento

25. LAB2 Use EjContFourier Verifique la propiedad del escalamiento

26. Propiedades de la FT 4. Desplazamiento

27. Propiedades de la FT 4. Desplazamiento

28. LAB3 Use EjContFourier Verifique la propiedad del desplazamiento

29. Propiedades de la FT 5. Convolución

30. Propiedades de la FT 7. Modulación

31. Transformada de Fourier discreta (DFT) Se define la transformada de Fourier discreta como Y su inversa como

32. Transformada Rápida de Fourier (FFT) DFT de elementos pares DFT de elementos impares

33. Transformada Rápida de Fourier DFT de N puntos 2 DFTs de N/2 puntos

34. Transformada Rápida de Fourier

35. Implementación Matlab Normalización distinta Origen es primer elemento

36. Normalización distinta Lo más común Matlab

37. Origen es primer elemento Humanos Computadores

38. Origen es primer elemento Humanos Computadores

39. LAB4 Encuentre la DFT de Grafique las partes real e imaginaria Ayuda: use una ventana (Hamming por ejemplo) para evitar distorsiones de Gibbs

40. Solución

41. Conexión entre DFT y FT Muestrear es multiplicar por Su transformada es

42. Conexión entre DFT y FT

43. Conexión entre DFT y FT

44. LAB5 Use EjContFourier Experimente con diferentes frecuencias de muestreo

45. Conexión entre DFT y FT ¿Qué significa una frecuencia discreta? El periodo debe ser un múltiplo entero de T

46. Teorema de Nyquist “ Las muestras discretas uniformemente espaciadas de una señal de ancho de bada limitado son una representación completa de la señal si el ancho de banda es menor a la mitad de la frecuencia de muestreo.” (Shannon) Picture: Ruye Wang

47. Aliasión Frecuencia de muestreo mayor a Nyquist

48. Aliasión Frecuencia de muestreo mayor a Nyquist: recuperación de la señal

49. 6.6 Consideraciones prácticas: aliasión Frecuencia de muestreo de Nyquist

50. Aliasión Frecuencia de muestreo de Nyquist: recuperación de la señal

51. Aliasión Frecuencia de muestreo menor a Nyquist

52. Aliasión Frecuencia de muestreo menor a Nyquist: recuperación de la señal

53. Primera aparición “ A Mathematical Theory of Communication”, Shannon 1948 Claude Shannon (1916– 2001)

54. Shannon honra a Nyquist “ Communication in the Presence of Noise”, Shannon 1949 1928: Harry Nyquist (1889 – 1976)