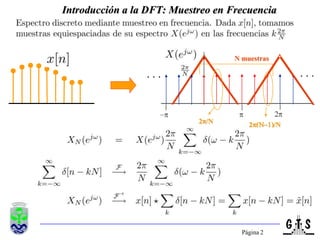
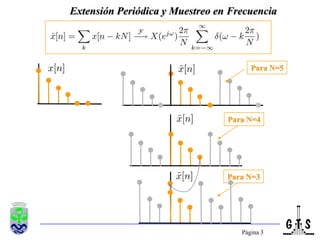
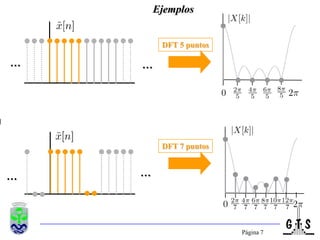
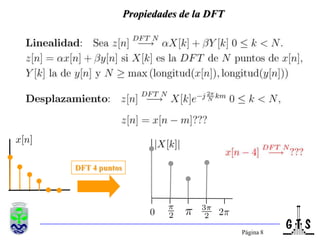
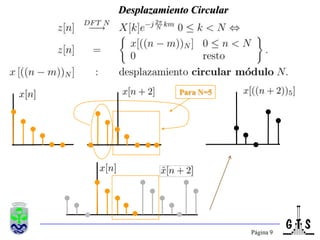
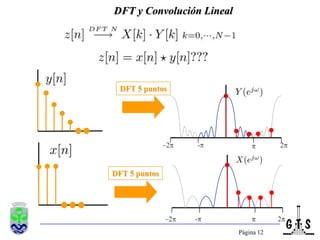
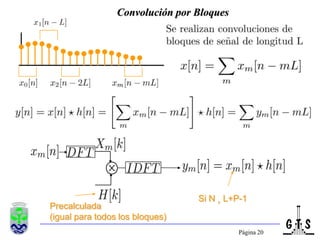
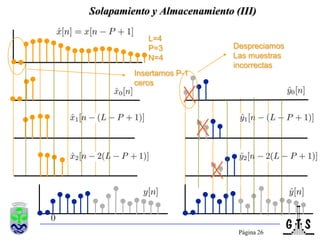
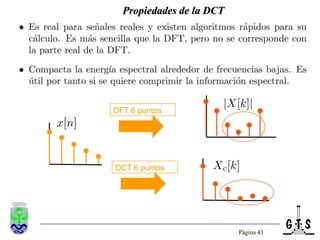
Este documento trata sobre el tratamiento digital de señales y se enfoca en la transformada discreta de Fourier (DFT). Explica la formulación y propiedades de la DFT, métodos de filtrado lineal basados en la DFT, y la transformada rápida de Fourier (FFT). También introduce la transformada discreta del coseno (DCT), incluyendo sus relaciones con la DFT y sus aplicaciones como la compactación espectral en compresión de imágenes como JPEG.




![Página 10Dualidad y Simetrías de la DFTN=4Como x[n] es real, para que X[k] sea real se debe cumplir que x[n]=x[((-n))N]Se cumple en todos los casos, luego la DFT es real](https://image.slidesharecdn.com/tema2-100531052306-phpapp01/85/Tema2-10-320.jpg)









![Página 22L muestrasSin solaparP-1 Muestas solapadasDFT x H[k]Y DFT-1Solapamiento y SumaL=4P=3N=6L2L0L+P-20LL2L+P-22L2L3L+P-2](https://image.slidesharecdn.com/tema2-100531052306-phpapp01/85/Tema2-22-320.jpg)





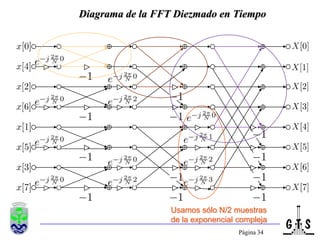
![Página 29FFT por Diezmado en Tiempo(H[k])(G[k])](https://image.slidesharecdn.com/tema2-100531052306-phpapp01/85/Tema2-29-320.jpg)





![Página 36Transformada Coseno (DCT): IntroducciónSiempre ceropara N parya que H[N/2]=H*[N/2] N/2-1 valores Redundantes(si N par)N/2-1 valores Redundantes(si N par)Siempre ceroya que H[0]=H*[0]](https://image.slidesharecdn.com/tema2-100531052306-phpapp01/85/Tema2-36-320.jpg)




![Página 42 Relación Entre DFT y DCT-2: EjemploDesplazamiento de media muestraDFT-1 2NDFT 2NComplejaPero X2[k]=X2*[-k]Real y simétrica](https://image.slidesharecdn.com/tema2-100531052306-phpapp01/85/Tema2-42-320.jpg)
