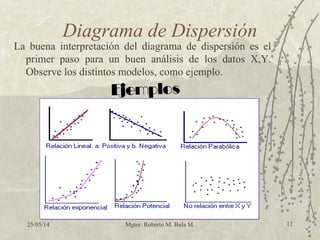
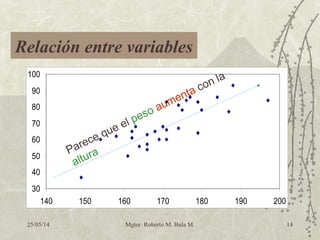
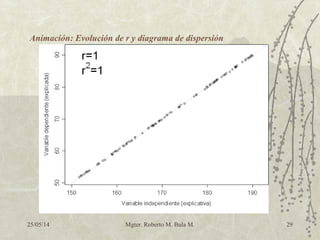
El análisis de regresión es una herramienta estadística que permite cuantificar la relación entre dos o más variables, utilizada en diversas disciplinas como negocios y ciencias naturales. Estudia si las variables están asociadas y permite predecir el comportamiento de una variable dependiente en función de una o más variables independientes. Se inicia con la representación de datos en un diagrama de dispersión y se utilizan coeficientes de correlación y determinación para evaluar la calidad de la predicción.