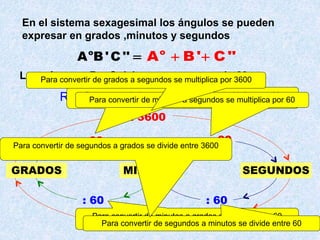
Este documento explica los diferentes sistemas de medición angular, incluyendo el sistema sexagesimal, centesimal y radial. Describe cómo convertir entre grados, minutos, segundos y radianes en cada sistema, y las relaciones y factores de conversión entre ellos. También cubre conceptos básicos de ángulos complementarios y suplementarios.

1. TRIGONOMETRIA

3. ÁNGULO TRIGONOMÉTRICO
• EL ÁNGULO
TRIGONOMÉTRICO
SE OBTIENE
GIRANDO UN RAYO
ALREDEDOR DE SU
ORIGEN.
SENTIDO DE GIRO HORARIO
SENTIDO DE GIRO ANTIHORARIO
OA : LADO INICIAL
)O
A
B
) POSITIVO
) NEGATIVO
OB : LADO FINAL
O: VÉRTICE

4. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA SEXAGESIMAL (SISTEMA INGLÉS)
o
1GRADO : MINUTO : '
1 SEGUNDO : "
1
'o
601  "'
601  "o
36001 
1vuelta=
o
360
EQUIVALENCIAS

5. En el sistema sexagesimal los ángulos se pueden
expresar en grados ,minutos y segundos
o
A B'C '' o
A B' C '' 
Los números B y C deben ser menores de 60
RELACIONES DE CONVERSIÓN
GRADOS MINUTOS SEGUNDOS
x 60 x 60
x 3600
: 60 : 60
: 3600
Para convertir de grados a minutos se multiplica por 60
Para convertir de minutos a grados se divide entre 60
Para convertir de minutos a segundos se multiplica por 60
Para convertir de segundos a minutos se divide entre 60
Para convertir de grados a segundos se multiplica por 3600
Para convertir de segundos a grados se divide entre 3600

6. EJEMPLO :
o
20 36' 45'' 
EXPRESAR EN GRADOS SEXAGESIMALES
o ' ''
20 36 45   
o o
o 36 45
20
60 3600
   
o o
o 3 1
20
5 80
  
o
1649
80
 CONCLUSIÓN:
RELACIÓN ENTRE LOS NÚMEROS DE GRADOS ,MINUTOS y
SEGUNDOS
NÚMERO DE GRADOS SEXAGESIMALES = S
NÚMERO DE MINUTOS SEXAGESIMALES ( m ) = 60S
NÚMERO DE SEGUNDOS SEXAGESIMALES ( p ) = 3600S
Al número 36 se le divide entre 60 y
Al número 45 se le divide entre 3600

7. EJEMPLO
Calcular la medida de un ángulo en el sistema sexagesimal ,
sabiendo que su número de minutos sexagesimales más el
doble de su número de grados sexagesimales es igual a 155.
SOLUCIÓN
Sea S = número de grados sexagesimales
Entonces el número de minutos sexagesimales = 60S
Dato :
155 5(31)
S
62 2(31)
 
60S 2S 155  62S 155
5
S
2

El ángulo mide :
5º 4º 60'
2
2 2
º 30' 

8. ESTAN ENTENDIENDO?
NOSREPITE PORFAVOR

9. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA CENTESIMAL (SISTEMA FRANCÉS)
g
1GRADO : MINUTO :
m
1 SEGUNDO :
s
1
g m
1 100
m s
1 100 g s
1 10000
1vuelta=
g
400
EQUIVALENCIAS

10. En el sistema centesimal los ángulos se pueden
expresar en grados ,minutos y segundos
g m s
A B C g m s
A B C  
Los números B y C deben ser menores de 100
RELACIONES DE CONVERSIÓN
GRADOS MINUTOS SEGUNDOS
x 100 x 100
x 10 000
: 100 : 100
: 10 000
Para convertir de grados a minutos se multiplica por 100
Para convertir de minutos a grados se divide entre 100
Para convertir de minutos a segundos se multiplica por 100
Para convertir de segundos a minutos se divide entre 100
Para convertir de grados a segundos se multiplica por 10000
Para convertir de segundos a grados se divide entre 10000

11. RELACIÓN ENTRE LOS NÚMEROS DE GRADOS ,MINUTOS
y SEGUNDOS
NÚMERO DE GRADOS CENTESIMALES = C
NÚMERO DE MINUTOS CENTESIMALES ( n ) = 100C
NÚMERO DE SEGUNDOS CENTESIMALES ( q ) = 10 000C
RELACIÓN ENTRE LOS SISTEMAS SEXAGESIMAL Y
CENTESIMAL
gO
109  m'
5027  s"
25081 
GRADOS MINUTOS SEGUNDOS
109
CS

5027
nm

25081
qp

SABEMOS QUE
SIMPLIFICANDO SE OBTIENE
g
180º 200
g
9º 10
SABES QUE :
g
9(1º ) 10(1 )
' m
9(60 ) 10(100 )
g
9º 10
' m
27 50
SABES QUE :
g
9º 10
g
9(1º ) 10(1 )
'' S
9(3600 ) 10(10000 )
'' s
81 250

12. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA RADIAL (SISTEMA CIRCULAR)
UN RADIÁN ES LA
MEDIDA DEL
ÁNGULO CENTRAL
QUE SUBTIENDE
EN CUALQUIER
CIRCUNFERENCIA
UN ARCO DE
LONGITUD IGUAL
AL RADIO.
.. 1rad
1vuelta 2 rad 
o ' ''
1rad 57 17 45
R
R
R)
EN ESTE SISTEMA
LA UNIDAD DE
MEDIDA ES EL
RADIÁN.

13. RELACIÓN ENTRE LOS TRES SISTEMAS
0 g
180 200 rad  
ESTA RELACIÓN SE USA PARA CONVERTIR DE UN
SISTEMA A OTRO.
EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR A RADIANES
0
A) 54 
O
54
o
rad
180
 
 
 

3
rad
10

g
B) 125 
g
rad
200
 
 
 

5
rad
8
g
125
EJEMPLOS
SABES QUE EL ÁNGULO DE UNA
VUELTA MIDE :
SIMPLIFICANDO SE OBTIENE :
g
360º 400 2 rad  

14. EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR AL SISTEMA
SEXAGESIMAL
A)
2
rad
3

...........
o
2(180 )
3
 o
120
g
B)70 .................
g
70
o
g
9
10
 
 
 
 o
63
EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR AL SISTEMA
CENTESIMAL
A)
3
rad
4

...........
g
3(200 )
4
 g
150
o
B)27 ................ o
27
g
o
10
9
 
 
 
 g
30

15. FACTORES DE CONVERSIÓN
DE GRADOS SEXAGESIMALES
A RADIANES
DE GRADOS SEXAGESIMALES
A CENTESIMALES
DE GRADOS CENTESIMALES
A RADIANES
DE GRADOS CENTESIMALES
A SEXAGESIMALES
DE RADIANES A GRADOS
SEXAGESIMALES
DE RADIANES A GRADOS
CENTESIMALES
o
rad
180

g
o
10
9
g
rad
200

o
g
9
10
o
rad 180 
g
rad 200 

16. ESTAN ENTENDIENDO?
NOSREPITE PORFAVOR

17. FÓRMULA DE CONVERSIÓN
S
180

C
200

R

S : NÚMERO DE GRADOS SEXAGESIMALES
C : NÚMERO DE GRADOS CENTESIMALES
R : NÚMERO DE RADIANES
EJEMPLO
CALCULAR EL NÚMERO DE RADIANES DE UN ÁNGULO ,SI SE CUMPLE:
8R
3S 2C 37  

EN ESTE TIPO DE PROBLEMA SE DEBE USAR LA FÓRMULA DE
CONVERSIÓN
SOLUCIÓN

18. S C R
180 200
  

K
S k180
C k200
R k 
SE REEMPLAZA EN EL DATO DEL PROBLEMA
8( k)
3(180k) 2(200k) 37

  

,SIMPLIFICANDO SE OBTIENE
148k 37
1
k
4

FINALMENTE EL NÚMERO DE RADIANES ES : R 
1
4
 
  
  4

S k9
C k10
R
0
k
2


NOTA : LA FÓRMULA DE CONVERSIÓN EN ALGUNOS CASOS
CONVIENE EXPRESARLA DE LA SIGUIENTE MANERA
S
9

C
10

20R


19. OTRAS RELACIONES IMPORTANTES
* ÁNGULOS COMPLEMENTARIOS SUMAN : o g
90 100 rad
2

 
* ÁNGULOS SUPLEMENTARIOS SUMAN :
O g
180 200 rad  
* EQUIVALENCIAS USUALES:
o
rad 60
3

 o
rad 30
6

o
rad 45
4


SISTEMA
SEXAGESIMAL
CENTESIMAL
RADIAL
COMPLEMENTO SUPLEMENTO
S
C
R
90 - S 180 - S
100 - C 200 - C
R
2

 R 

20. EJERCICIOS
1. CALCULAR :
g
45º rad
12E
50 33º




SOLUCIÓN
Para resolver este ejercicio la idea es convertir cada uno
de los valores dados a un solo sistema ,elegimos el
SISTEMA SEXAGESIMAL
rad
12


180º
12
15º g
50; 45º
Reemplazamos en E
45º 15º
E
45º 33º

 

60º
12º
 5
g
9º
( )
10


21. 2. El número de grados sexagesimales de un ángulo más
el triple de su número de grados centesimales es 78,
calcular su número de radianes
SOLUCIÓN
Sea S = número de grados sexagesimales
C = número de grados centesimales
Sabes que : S C
9 10
 = K y
Dato : S + 3C = 78
S = 9K C = 10K
9K + 3( 10K ) = 78 39K = 78 K = 2
El número de radianes es :
k
R
20


2
R
20

 
10


22. 3. Determinar si el enunciado es verdadero o falso
A ) rad 180 
B ) El complemento de es
g
30 g
70
C )
g g
24º 2º
36 3

D )
rad
Los ángulos interiores de un triángulo
suman
E ) 180º 
F ) g
1º 1
G ) El número de grados sexagesimales de un ángulo es
igual al 90% de su número de grados centesimales

23. TRIGONOMETRIA
CONTEMPORANEA