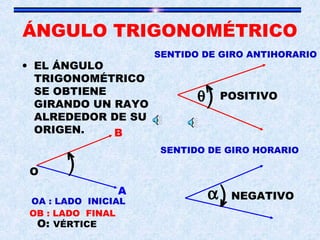
Este documento presenta los diferentes sistemas de medición angular, incluyendo el sistema sexagesimal, centesimal y radial. Explica conceptos como ángulo trigonométrico, sentidos de giro, conversiones entre sistemas y fórmulas. También incluye ejemplos de conversiones entre grados, minutos, segundos y radianes.

1. TRIGONOMETRIA
CONTEMPORANEA
PROFESOR:
RUBÉN ALVA CABRERA
rubalva@hotmail.com

3. ÁNGULO TRIGONOMÉTRICO
• EL ÁNGULO
TRIGONOMÉTRICO
SE OBTIENE
GIRANDO UN RAYO
ALREDEDOR DE SU
ORIGEN.
SENTIDO DE GIRO ANTIHORARIO
SENTIDO DE GIRO HORARIO
) O
B
A
<
OA : LADO INICIAL
) <q POSITIVO
)<a NEGATIVO
OB : LADO FINAL
O: VÉRTICE

4. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA SEXAGESIMAL (SISTEMA INGLÉS)
GRADO :1 o MINUTO : 1' SEGUNDO : 1"
EQUIVALENCIAS
1o = 60' 1' = 60" 1o = 3600"
1vuelta=360o

5. En el sistema sexagesimal los ángulos se pueden
expresar en grados ,minutos y segundos
AoB'C'' = Ao + B'+ C''
Los números B y C deben ser menores de 60
Para convertir de grados a segundos se multiplica por 3600
RELACIONES DE CONVERSIÓN
Para convertir de grados a minutos se multiplica por 60
Para convertir de minutos a segundos se multiplica por 60
x 3600
x 60 x 60
Para convertir de segundos a grados se divide entre 3600
<
<
GRADOS MINUTOS SEGUNDOS
: 60 : 60
: 3600
<
<
<
<
<
<
<
<
<
<
Para convertir de minutos a grados se divide entre 60
Para convertir de segundos a minutos se divide entre 60

6. EJEMPLO : q = 20o36' 45''
EXPRESAR q EN GRADOS SEXAGESIMALES
q = 20o + 36' + 45''
20o 36 45
o o
q = + +
60 3600
20o 3 1
o o
= + +
1649o
80
5 80
Al número 36 se le divide entre 60 y
Al número 45 se le divide entre 3600
CONCLUSIÓN: q =
RELACIÓN ENTRE LOS NÚMEROS DE GRADOS ,MINUTOS y
SEGUNDOS
NÚMERO DE GRADOS SEXAGESIMALES = S
NÚMERO DE MINUTOS SEXAGESIMALES ( m ) = 60S
NÚMERO DE SEGUNDOS SEXAGESIMALES ( p ) = 3600S

7. EJEMPLO
Calcular la medida de un ángulo en el sistema sexagesimal ,
sabiendo que su número de minutos sexagesimales más el
doble de su número de grados sexagesimales es igual a 155.
SOLUCIÓN
Sea S = número de grados sexagesimales
Entonces el número de minutos sexagesimales = 60S
Dato :
60S + 2S = 155 62S = 155
S 155 5(31)
= =
62 2(31)
S 5
2
=
El ángulo mide :
5º 4º60' 2
2 2
= = º 30'

8. ESTAN
ENTENDIENDO ?
NO REPITE POR
FAVOR

9. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA CENTESIMAL (SISTEMA FRANCÉS)
1g GRADO : MINUTO :
1m SEGUNDO :
1s
EQUIVALENCIAS
1g = 100m 1m = 100s 1g = 10000s
1vuelta= 400g

10. En el sistema centesimal los ángulos se pueden
expresar en grados ,minutos y segundos
AgBmCs = Ag + Bm + Cs
Los números B y C deben ser menores de 100
Para convertir de grados a segundos se multiplica por 10000
RELACIONES DE CONVERSIÓN
Para convertir de grados a minutos se multiplica por 100
Para convertir de minutos a segundos se multiplica por 100
x 10 000
Para convertir de segundos a grados se divide entre 10000
x 100 x 100
<
<
GRADOS MINUTOS SEGUNDOS
: 100 : 100
: 10 000
<
<
<
<
<
<
<
<
<
<
Para convertir de minutos a grados se divide entre 100
Para convertir de segundos a minutos se divide entre 100

11. RELACIÓN ENTRE LOS NÚMEROS DE GRADOS ,MINUTOS
y SEGUNDOS
SABES QUE :
SABES QUE :
NÚMERO DE GRADOS 9º CENTESIMALES = 10g
180º = 200g
= C
NÚMERO DE MINUTOS 9(1º ) CENTESIMALES = 10(1g )
( n ) = 100C
NÚMERO DE SEGUNDOS 9(60' ) = 10(CENTESIMALES 100m)
( q ) = 10 000C
RELACIÓN ENTRE LOS SISTEMAS SEXAGESIMAL Y
CENTESIMAL
9O = 10g 27' = 50m 81" = 250s
GRADOS MINUTOS SEGUNDOS
S C = 27 50
9 10
m n =
p q =
81 250
SABEMOS QUE
SIMPLIFICANDO SE OBTIENE
9º = 10g
27' = 50m
9º = 10g
9(1º ) = 10(1g )
9(3600'' ) = 10(10000S )
81'' = 250s

12. SISTEMAS DE MEDICIÓN
ANGULAR
• SISTEMA RADIAL (SISTEMA CIRCULAR)
UN RADIÁN ES LA
MEDIDA DEL
ÁNGULO CENTRAL
QUE SUBTIENDE
EN CUALQUIER
CIRCUNFERENCIA
UN ARCO DE
LONGITUD IGUAL
AL RADIO.
R
) R
.. 1rad
R
1vuelta = 2prad
1rad = 57o17'45''
EN ESTE SISTEMA
LA UNIDAD DE
MEDIDA ES EL
RADIÁN.

13. RELACIÓN ENTRE LOS TRES SISTEMAS
1800 = 200g = prad
ESTA RELACIÓN SE USA PARA CONVERTIR DE UN
SISTEMA A OTRO.
EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR A RADIANES
A)q = 540
rad
180
æ p ö
çè ø¸ = 3 rad
54O o
p
10
B)f = 125g
æ p ö
çè ø¸ = 5 rad
125g p
rad
200
g
8
EJEMPLOS
SABES QUE EL ÁNGULO DE UNA
VUELTA MIDE :
SIMPLIFICANDO SE OBTIENE :
360º = 400g = 2prad

14. EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR AL SISTEMA
SEXAGESIMAL
A) 2 rad
p ...........
3
2(180o )
3 = 120o
B)70g ................. 70g
9
10
o
g
æ ö
ç ¸
è ø
= 63o
EN CADA UNO DE LOS SIGUIENTES CASOS CONVERTIR AL SISTEMA
CENTESIMAL
A) 3 p
rad
4
...........
3(200g )
4 =150g
B)27o ................ 27o
10
9
g
o
æ ö
ç ¸
è ø
=30g

15. FACTORES DE CONVERSIÓN
DE GRADOS SEXAGESIMALES
A RADIANES
DE GRADOS SEXAGESIMALES
A CENTESIMALES
DE GRADOS CENTESIMALES
A RADIANES
DE GRADOS CENTESIMALES
A SEXAGESIMALES
DE RADIANES A GRADOS
SEXAGESIMALES
DE RADIANES A GRADOS
CENTESIMALES
p
rad
180
o
10
9
g
o
p
rad
200
g
9
10
o
g
prad = 180o
prad = 200g

16. ESTAN
ENTENDIENDO ?
NO REPITE POR
FAVOR

17. FÓRMULA DE CONVERSIÓN
S
180
= C
200
= R
p
S : NÚMERO DE GRADOS SEXAGESIMALES
C : NÚMERO DE GRADOS CENTESIMALES
R : NÚMERO DE RADIANES
EJEMPLO
CALCULAR EL NÚMERO DE RADIANES DE UN ÁNGULO ,SI SE CUMPLE:
3S - 2C + 8R = 37
p
SOLUCIÓN
EN ESTE TIPO DE PROBLEMA SE DEBE USAR LA FÓRMULA DE
CONVERSIÓN

18. S C R
180 200
p K
= = =
S = 180k
C = 200k
R = pk
SE REEMPLAZA EN EL DATO DEL PROBLEMA
3(180k) - 2(200k) + 8(pk) = 37
p
,SIMPLIFICANDO SE OBTIENE
148k = 37 k 1
4
=
FINALMENTE EL NÚMERO DE RADIANES ES : R =
1
4
p
p æ ö = çè ø¸ 4
S = 9k
C = 10k
R
k
2
= p
0
NOTA : LA FÓRMULA DE CONVERSIÓN EN ALGUNOS CASOS
CONVIENE EXPRESARLA DE LA SIGUIENTE MANERA
S
= C
= 20R
9
10
p

19. OTRAS RELACIONES IMPORTANTES
Ú Ú p
* ÁNGULOS COMPLEMENTARIOS SUMAN : 90o 100g rad
2
* ÁNGULOS SUPLEMENTARIOS SUMAN : 180O Ú 200g Ú prad
p- p - R
* EQUIVALENCIAS USUALES:
rad 45o p =
4
p = rad 30o
rad 60o
3
6
p =
SISTEMA
SEXAGESIMAL
CENTESIMAL
RADIAL
COMPLEMENTO SUPLEMENTO
S
C
R
90 - S 180 - S
100 - C 200 - C
R
2

20. EJERCICIOS
1. CALCULAR :
+ p
45º rad
E 12
50 g
33º
=
-
SOLUCIÓN
Para resolver este ejercicio la idea es convertir cada uno
de los valores dados a un solo sistema ,elegimos el
SISTEMA SEXAGESIMAL
p = 180º
rad
12
12
( 9º )
10
=15º ; 50g 45º
Reemplazamos en E
E 45º 15º
= + =
45º -
33º
60º
12º
= 5
g
=

21. 2. El número de grados sexagesimales de un ángulo más
el triple de su número de grados centesimales es 78,
calcular su número de radianes
SOLUCIÓN
Sea S = número de grados sexagesimales
C = número de grados centesimales
Sabes que : S C
= = K y
9 10
Dato : S + 3C = 78
S = 9K C = 10K
9K + 3( 10K ) = 78 39K = 78 K = 2
El número de radianes es :
R k
= p R 2
20
= p =
20
p
10

22. 3. Determinar si es verdadero o falso
A ) prad = 180
B ) El complemento de es 30g 70g
C )
24º 2º
=
36 g 3
g
D )
Los ángulos interiores de un triángulo
suman
prad
E ) p = 180º
F ) 1º > 1g
G ) El número de grados sexagesimales de un ángulo es
igual al 90% de su número de grados centesimales

23. TRIGONOMETRIA
CONTEMPORANEA
rubalva@hotmail.com