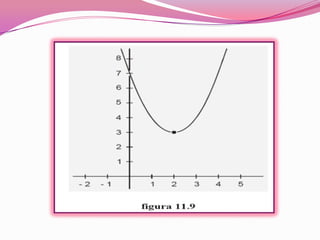
Este documento explica cómo calcular los máximos y mínimos de una función. Indica que los máximos y mínimos ocurren cuando la derivada de la función es cero. Esto da los valores críticos, los cuales pueden ser máximos o mínimos dependiendo de si la derivada cambia de positiva a negativa o viceversa. Proporciona un ejemplo para ilustrar el proceso de encontrar el máximo y mínimo de la función y=x2 −4x+7.

1. Máximos y mínimosde una función

2. Máximos y mínimos de una funciónEntre los valores que puede tener una función (Y) puede haber uno que sea el mas grande y otro que sea el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo absolutos. Una función puede tener uno, ninguno o varios puntos críticos.En síntesis, se puede formular la siguiente regla para calcular los máximos y/o mínimos de una función f(x):

3. Para calcular los máximos y/o mínimos de una función f(x):1) Se deriva la función y = f( x ) y se iguala a cero la derivada.2) Se resuelve la ecuación resultante del paso anterior. Las raícesencontradas se llaman valores críticos y son los que por tenertangente con pendiente cero (tangentes horizontales), puedenser máximos o mínimos.3) Para investigar cada valor crítico si es máximo o mínimo: a) Se toma un valor un poco menor a ese valor crítico y sesustituye en la derivada. Luego se toma un valor unpoco mayor y se sustituye en la derivada. b) Si el valor de la derivada cambia de positivo a negativo,el valor crítico en análisis es un máximo; si cambia denegativo a positivo, es un mínimo.

4. Ejemplo de aplicaciónEjemplo : Hallar los valores máximos y/o mínimos de la función y=x2 −4x+7.Graficando la función anterior se obtiene la parábola de la figura 11.9. Lo que deberá confirmarse aplicando el procedimiento.

6. Solución del problemaPaso 1: Derivando la función e igualando a cero:dy /dx = 2x – 4=0Paso 2: Resolviendo 2x - 4 = 0, se llega a que x = 2. - Este es el valor crítico.

7. Paso 3a: Dando primero un valor un poco más pequeño que x = 2, por ejemplo, con x = 1 y sustituyendo en la derivada: dy/ dx = 2(1) -4 =2 luego con un valor un poco mayor que x = 2, por ejemplo con x = 3 y sustituyendo en la derivada:dy /dx = 2(3)- 4 =2

8. Paso 3b: Como la derivada cambió de signo de negativo a positivo significa que existe un mínimo en el valor crítico que se analiza, es decir, hay un mínimo en x = 2.Nota de solución: tiene solamente un mínimo.

9. UNIVERSIDAD ESTATAL DEL VALLE DE ECATEPECIngeniería en Comunicación MultimediaCampos Alcantar Nallely1442 mayo 2010