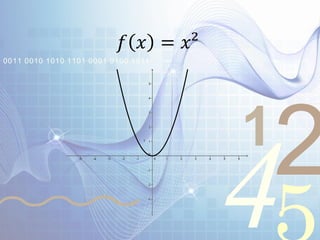
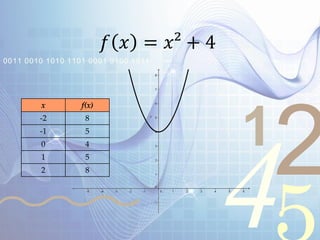
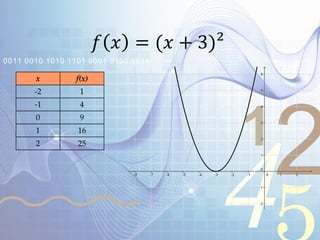
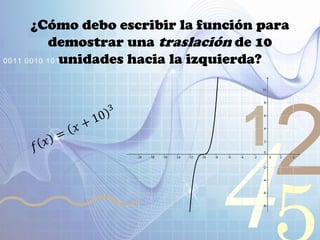
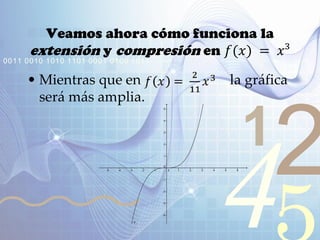
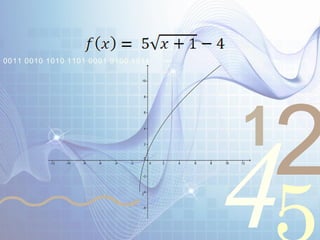
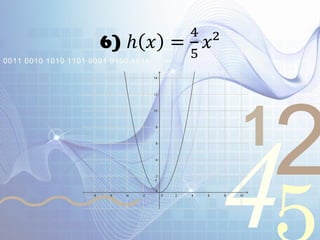
El documento explica las funciones y sus transformaciones. Define una función como una relación que asigna exactamente un valor del rango a cada valor del dominio. Describe las transformaciones básicas de funciones como la reflexión, traslación, extensión y compresión. Explica cómo estas transformaciones afectan las gráficas de funciones como f(x)=x^2, f(x)=|x|, y f(x)=√x.

1. 421
0011 0010 1010 1101 0001 0100 1011
4210011 0010 1010 1101 0001 0100 1011
Funciones
Prof. R. Padilla

2. 421
0011 0010 1010 1101 0001 0100 1011
Funciones
• Función: relación que asigna
exactamente un valor del rango a cada
valor del dominio.

3. 421
0011 0010 1010 1101 0001 0100 1011
Funciones
• Relación  cualquier conjunto de pares
ordenados. Ejemplo: 𝑥, 𝑦
• Dominio  son todos los valores de x
en una relación.
• Rango  son todos los valores de y en
una relación.

4. 421
0011 0010 1010 1101 0001 0100 1011
Relación vs. Función
• Ejemplos:
– {(2,-3), (4, 3), (5,6), (2,8)}
– {(3,5) , (8,4), (9,4), (1,5)}
– {(1,-2), (3, -2), (5, -2)}

5. 421
0011 0010 1010 1101 0001 0100 1011
La prueba de la recta
vertical

6. 421
0011 0010 1010 1101 0001 0100 1011
La prueba de la recta
vertical

7. 421
0011 0010 1010 1101 0001 0100 1011
Funciones
• Las funciones se pueden transformar
utilizando la reflexión, la traslación, la
extensión y la compresión.
• Todas esas transformaciones forman
una familia de funciones.

8. 421
0011 0010 1010 1101 0001 0100 1011
FUNCIONES BÁSICAS Y SUS
FAMILIAS

9. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥²

10. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = −𝑥²
• ¿Qué tiene de diferente la función?
• ¿Qué efecto tiene ese negativo?
• ¿De qué forma altera la gráfica con
respecto a la función original?

11. 421
0011 0010 1010 1101 0001 0100 1011
El negativo en la función crea una
reflexión de la gráfica en el eje de x
𝑓 𝑥 = −𝑥²

12. 421
0011 0010 1010 1101 0001 0100 1011
f(x) = x² + 4
Y esta función,
¿qué tiene de diferente?

13. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥² + 4
x f(x)x f(x)
-2 8
-1 5
0 4
1 5
2 8

14. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥² + 4
• El 4, por ser positivo, ocasiona una
traslación de la función.
• La función se trasladó 4 unidades hacia
arriba con respecto a su posición
original.
• En conclusión, la suma o resta de
constantes hará una traslación en el eje
de y hacia arriba o hacia abajo
respectivamente.

15. 421
0011 0010 1010 1101 0001 0100 1011
El próximo miembro en la
familia de 𝑓 𝑥 = 𝑥² es
𝑓 𝑥 = (𝑥 + 3)²
• ¿Qué crees que pasará?
• ¿Se trasladará también hacia arriba
como ocurrió cuando le sumamos 4 a la
función?

16. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = (𝑥 + 3)²
x f(x)x f(x)
-2 1
-1 4
0 9
1 16
2 25

17. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = (𝑥 + 3)²
• A diferencia de la función anterior, tanto el 3
como la x están siendo afectadas por el
exponencial.
• En este caso, la función se traslada hacia la
izquierda. Exactamente 3 unidades.
• Cuando se le suma o resta una constante
dentro del paréntesis, esto crea una traslación
en el eje de x.

18. 421
0011 0010 1010 1101 0001 0100 1011
¿Cuál de estas funciones muestra
una traslación hacia la derecha?
A. f(x)= x² - 8
B. f(x) = (x – 8)²

19. 421
0011 0010 1010 1101 0001 0100 1011
x f(x)
-2 8
-1 2
0 0
1 2
2 8
x f(x)
Te presento al último miembro de la
familia de la función 𝑓 𝑥 = 𝑥²
• Grafiquemos f(x) = 2x² y veamos qué
pasa.

20. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥²
• 2 es un número mayor que 1. ¿Qué
crees que ocurrirá si el número es
menor que 1?
• Por ejemplo: 𝑓 𝑥 =
1
2
𝑥²
x f(x)x f(x)
-2 2
-1 ½
0 0
1 ½
2 1

21. 421
0011 0010 1010 1101 0001 0100 1011
Transformaciones
• Estas transformaciones se llaman
extensión y compresión.
• La extensión ocurre cuando el coeficiente
es mayor que 1.
• La compresión ocurre cuando el
coeficiente es mayor que 0 pero menor
que 1.

22. 421
0011 0010 1010 1101 0001 0100 1011
Transformaciones
• Mientras más grande sea el coeficiente más
estrecha será su gráfica. Se acercará más al eje
de y, sin nunca tocarlo.
• Mientras más cerca de 0 sea el coeficiente,
más amplia será su gráfica. Se acercará más al
eje de x, pero nunca lo tocará.

23. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³

24. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³
• Si nos dejamos llevar por las
transformaciones de f(x) = x² ; ¿Qué
crees que pasará si le añadimos un
negativo?
• ¿Cómo será la gráfica de f(x) = -x³?

25. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³
• El negativo de la función crea una
reflexión de la gráfica en el eje de x.

26. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³
• ¿Qué pasará si le sumamos o restamos
una constante a la función?
• Por ejemplo:
• f(x) = x³ + 1
• f(x) = x³ - 3

27. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³
• Al igual que en la función f(x) = x² + 4, la
suma o resta de una constante hará que
la gráfica de la función se traslade.
• En el caso de f(x) = x³ + 1 se trasladará
exactamente 1 unidad hacia arriba.
• En f(x) = x³ - 3, la función se trasladará
exactamente 3 unidades hacia abajo de
la función básica .

28. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³ + 1

29. 421
0011 0010 1010 1101 0001 0100 1011
𝑓 𝑥 = 𝑥³ − 3

30. 421
0011 0010 1010 1101 0001 0100 1011
¿Puedes imaginar que
pasará en 𝑓 𝑥 = (𝑥 − 5)³?
• La función
básica se
trasladará
exactamente 5
unidades
hacia la
derecha.

31. 421
0011 0010 1010 1101 0001 0100 1011
¿Cómo debo escribir la función para
demostrar una traslación de 10
unidades hacia la izquierda?

32. 421
0011 0010 1010 1101 0001 0100 1011
Veamos ahora cómo funciona la
extensión y compresión en 𝑓(𝑥) = 𝑥³
• Si graficamos f(x) = 10x³ notaremos que
la gráfica se hará más estrecha.

33. 421
0011 0010 1010 1101 0001 0100 1011
Veamos ahora cómo funciona la
extensión y compresión en 𝑓(𝑥) = 𝑥³
• Mientras que en la gráfica
será más amplia.

34. 421
0011 0010 1010 1101 0001 0100 1011
x f(x)
La próxima función básica
es 𝑓(𝑥) = |𝑥|
• Grafiquemos esta función:
x f(x)
-2 2
-1 1
0 0
1 1
2 2

35. 421
0011 0010 1010 1101 0001 0100 1011
𝑓(𝑥) = |𝑥|
• Ahora, veamos si ya entiendes las
transformaciones.
• ¿Cómo será cada una de las siguientes
gráficas?
 f(x) = -|x|
 f(x) = |x| + 6
 f(x) = |x + 6|
 f(x) = |x| - 9
 f(x) = |x - 9|

36. 421
0011 0010 1010 1101 0001 0100 1011
x f(x)
La última función básica es
• Grafiquemos esta función:
x f(x)
0 0
1 1
2 1.14
3 1.73
4 2

37. 421
0011 0010 1010 1101 0001 0100 1011
Practiquemos una vez más
las transformaciones
1) 𝑓 𝑥 = 𝑥 + 4
2) 𝑓 𝑥 = 𝑥 − 2
3) 𝑓 𝑥 = 𝑥 + 5
4) 𝑓 𝑥 = 𝑥 − 3
5) 𝑓 𝑥 = 15 𝑥
6) 𝑓 𝑥 =
1
10
𝑥

38. 421
0011 0010 1010 1101 0001 0100 1011
• Hay que destacar un detalle muy importante
en la extensión y compresión de .
• En la extensión, contrario a los casos
anteriores, la gráfica de la función se verá más
amplia a la vez que se acerca al eje de y.
• Mientras que en la compresión, la gráfica se ve
más estrecha a la vez que se acerca al eje de x.

39. 421
0011 0010 1010 1101 0001 0100 1011
Practiquemos ahora como graficar
funciones que tienen más de una
transformación
1) 𝑓 𝑥 = − 𝑥 − 3 2
+ 2
2) 𝑓 𝑥 = 5 𝑥 + 1 − 4
3) 𝑓 𝑥 =
1
10
𝑥 + 3 ³ + 5
4) 𝑓 𝑥 = − 𝑥 − 1 + 6

40. 421
0011 0010 1010 1101 0001 0100 1011

41. 421
0011 0010 1010 1101 0001 0100 1011

42. 421
0011 0010 1010 1101 0001 0100 1011

43. 421
0011 0010 1010 1101 0001 0100 1011

44. 421
0011 0010 1010 1101 0001 0100 1011
Práctica:
Grafica las siguientes funciones
1) 𝑓 𝑥 = 2𝑥 ² − 3
2) 𝑔 𝑥 = 𝑥 − 1 ²
3) ℎ 𝑥 = 𝑥 + 5 − 3
4) 𝑓 𝑥 = 𝑥 − 2
5) 𝑔 𝑥 = 𝑥² + 6
6) ℎ 𝑥 =
4
5
𝑥²
7) 𝑓 𝑥 = 𝑥 + 2 + 3
8) 𝑔 𝑥 = 𝑥³ − 2
9) ℎ 𝑥 = −𝑥2 − 1
10) 𝑓 𝑥 = − 𝑥 + 6
11) 𝑔 𝑥 = −(𝑥 − 4)²
12) ℎ 𝑥 = −
1
3
𝑥³

45. 421
0011 0010 1010 1101 0001 0100 1011
1) 𝑓 𝑥 = 2𝑥 ² − 3

46. 421
0011 0010 1010 1101 0001 0100 1011
2) 𝑔 𝑥 = 𝑥 − 1 ²

47. 421
0011 0010 1010 1101 0001 0100 1011
3) ℎ 𝑥 = 𝑥 + 5 − 3

48. 421
0011 0010 1010 1101 0001 0100 1011
4)𝑓 𝑥 = 𝑥 − 2

49. 421
0011 0010 1010 1101 0001 0100 1011
5) 𝑔 𝑥 = 𝑥² + 6

50. 421
0011 0010 1010 1101 0001 0100 1011
6) ℎ 𝑥 =
4
5
𝑥²

51. 421
0011 0010 1010 1101 0001 0100 1011
7) 𝑓 𝑥 = 𝑥 + 2 + 3

52. 421
0011 0010 1010 1101 0001 0100 1011
8) 𝑔 𝑥 = 𝑥³ − 2

53. 421
0011 0010 1010 1101 0001 0100 1011
9) ℎ 𝑥 = −𝑥2
− 1

54. 421
0011 0010 1010 1101 0001 0100 1011
10) 𝑓 𝑥 = − 𝑥 + 6

55. 421
0011 0010 1010 1101 0001 0100 1011
11) 𝑔 𝑥 = −(𝑥 − 4)²

56. 421
0011 0010 1010 1101 0001 0100 1011
12) ℎ 𝑥 = −
1
3
𝑥³