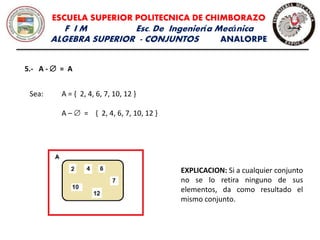
El documento explica los diagramas de Venn y las propiedades de la diferencia de conjuntos. Define la diferencia de conjuntos A - B como los elementos que pertenecen a A pero no a B. Presenta ejemplos para ilustrar las propiedades de la diferencia de conjuntos y resuelve un ejercicio con múltiples operaciones sobre conjuntos.